Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Xét hàm số $y =  – 2x + k\sqrt {{x^2} + 1} $a) Với $k = 3$ hãy lập bảng biến thiên của hàm số và xác định các tiệm cận của đồ thị.b) Với giá trị nào của $k$ thì hàm số có cực tiểu.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

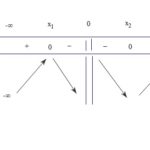
Đề bài: Xét hàm số $y =  - 2x + k\sqrt {{x^2} + 1} $a) Với $k = 3$ hãy lập bảng biến thiên của hàm số và xác định các tiệm cận của đồ thị.b) Với giá trị nào của $k$ thì hàm số có cực tiểu. Lời giải a) Với $k = 3$, ta có hàm số        $y = - 2x + 3\sqrt {{x^2} + 1} $Hàm số được xác định với mọi $x$ và có đạo hàm        $y' = - 2 + \frac{{3x}}{{\sqrt {{x^2} + 1} }} = … [Đọc thêm...] vềĐề: Xét hàm số $y =  – 2x + k\sqrt {{x^2} + 1} $a) Với $k = 3$ hãy lập bảng biến thiên của hàm số và xác định các tiệm cận của đồ thị.b) Với giá trị nào của $k$ thì hàm số có cực tiểu.

Đề: Cho hàm số: $y=\sqrt{x^{2}-8x+32}+\sqrt{x^{2}-6x+18}$Tìm giá trị nhỏ nhất của hàm số $y$.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số: $y=\sqrt{x^{2}-8x+32}+\sqrt{x^{2}-6x+18}$Tìm giá trị nhỏ nhất của hàm số $y$. Lời giải Ta có: $x^{2}-8x+32=(x-4)^{2}+16>0 \forall x.$       $x^{2}-6x+18=(x-3)^{2}+9>0 \forall x.$Tập xác định $D_{y}=R$Xét hai điểm sau: $\begin{cases} A(x-4;-4) \\ B(x-3;3)\end{cases} $$\Rightarrow \begin{cases} OA=\sqrt{x^{2}-8x+32} \\ OB=\sqrt{x^{2}-6x+18} \\AB= … [Đọc thêm...] vềĐề: Cho hàm số: $y=\sqrt{x^{2}-8x+32}+\sqrt{x^{2}-6x+18}$Tìm giá trị nhỏ nhất của hàm số $y$.

Đề:  Cho $a,b,c$ là các số thực thay đổi thuộc $[1;2]$Tìm giá trị nhỏ nhất , giá trị lớn nhất  của biểu thức $Q=(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$  

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:  Cho $a,b,c$ là các số thực thay đổi thuộc $[1;2]$Tìm giá trị nhỏ nhất , giá trị lớn nhất  của biểu thức $Q=(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$   Lời giải * Giá trị nhỏ nhấtTheo Cô-si $(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}) \geq 3\sqrt[3]{abc}.3.\frac{1}{\sqrt[3]{abc}}=9$ hay $Q \geq 9$Dấu đẳng thức có khi và chỉ khi $a=b=c>0$. Suy ra $\min Q=9$* … [Đọc thêm...] vềĐề:  Cho $a,b,c$ là các số thực thay đổi thuộc $[1;2]$Tìm giá trị nhỏ nhất , giá trị lớn nhất  của biểu thức $Q=(a+b+c)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$  

Đề: Cho hàm số         $y = \frac{{{x^2} – 2mx + m}}{{x + m}}$1)    Khảo sát sự biến thiên và vẽ đồ thị hàm số tương ứng với $m = 1$2)    Chứng minh rằng nếu đồ thị hàm số cắt $Ox$ tại $x = {x_0}$, thì hệ số góc của tiếp tuyến tại đó là:  $k = \frac{{2{x_0} – 2m}}{{{x_0} + m}}$3)    Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số cắt $Ox$ tại hai điểm và hai tiếp tuyến tại hai điểm đó vuông góc với nhau

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số         $y = \frac{{{x^2} - 2mx + m}}{{x + m}}$1)    Khảo sát sự biến thiên và vẽ đồ thị hàm số tương ứng với $m = 1$2)    Chứng minh rằng nếu đồ thị hàm số cắt $Ox$ tại $x = {x_0}$, thì hệ số góc của tiếp tuyến tại đó là:  $k = \frac{{2{x_0} - 2m}}{{{x_0} + m}}$3)    Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số cắt $Ox$ tại hai điểm và hai tiếp … [Đọc thêm...] vềĐề: Cho hàm số         $y = \frac{{{x^2} – 2mx + m}}{{x + m}}$1)    Khảo sát sự biến thiên và vẽ đồ thị hàm số tương ứng với $m = 1$2)    Chứng minh rằng nếu đồ thị hàm số cắt $Ox$ tại $x = {x_0}$, thì hệ số góc của tiếp tuyến tại đó là:  $k = \frac{{2{x_0} – 2m}}{{{x_0} + m}}$3)    Tìm tất cả các giá trị của tham số $m$ để đồ thị hàm số cắt $Ox$ tại hai điểm và hai tiếp tuyến tại hai điểm đó vuông góc với nhau

Đề: Cho hàm số $y=f(x)=\frac{ax+b}{cx+d}$,với $c \neq 0,D=ad-bc \neq 0.$ Chứng minh rằng đồ thị hàm số nhận điểm $I(-\frac{d}{c};\frac{a}{c})$ làm tâm đối xứng.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số $y=f(x)=\frac{ax+b}{cx+d}$,với $c \neq 0,D=ad-bc \neq 0.$ Chứng minh rằng đồ thị hàm số nhận điểm $I(-\frac{d}{c};\frac{a}{c})$ làm tâm đối xứng. Lời giải Ta có:Công thức dời trục:$\begin{cases} x=X-\frac{d}{c} \\ y=Y+\frac{a}{c}\end{cases}$Thay $x,y$ vào hàm số ta được:$Y+\frac{a}{c}=\frac{a(X-\frac{d}{c})+b}{c(X-\frac{d}{c})+d}$$\Leftrightarrow … [Đọc thêm...] vềĐề: Cho hàm số $y=f(x)=\frac{ax+b}{cx+d}$,với $c \neq 0,D=ad-bc \neq 0.$ Chứng minh rằng đồ thị hàm số nhận điểm $I(-\frac{d}{c};\frac{a}{c})$ làm tâm đối xứng.

Đề: $1)$  Lập bảng biến thiên và vẽ đồ thị ($C$) hàm số từ đường ($C$), suy ra đồ thị $({C^,})$ của hàm số  $y = {\log _2}\left( {x + 1} \right)$$ 2)$ Từ $({C^,})$, suy ra đồ thị $({C_1})$ của hàm số $y = \left| {{{\log }_2}\left( {x + 1} \right)} \right|$$ 3$) chứng minh rằng đồ thị $({C_2})$ của hàm số $y = {\log _2}\left| {x + 1} \right|$ nhận đường thẳng $x = – 1$ làm trục đối xứng. Vẽ $({C_2})$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: $1)$  Lập bảng biến thiên và vẽ đồ thị ($C$) hàm số từ đường ($C$), suy ra đồ thị $({C^,})$ của hàm số  $y = {\log _2}\left( {x + 1} \right)$$ 2)$ Từ $({C^,})$, suy ra đồ thị $({C_1})$ của hàm số $y = \left| {{{\log }_2}\left( {x + 1} \right)} \right|$$ 3$) chứng minh rằng đồ thị $({C_2})$ của hàm số $y = {\log _2}\left| {x + 1} \right|$ nhận đường … [Đọc thêm...] vềĐề: $1)$  Lập bảng biến thiên và vẽ đồ thị ($C$) hàm số từ đường ($C$), suy ra đồ thị $({C^,})$ của hàm số  $y = {\log _2}\left( {x + 1} \right)$$ 2)$ Từ $({C^,})$, suy ra đồ thị $({C_1})$ của hàm số $y = \left| {{{\log }_2}\left( {x + 1} \right)} \right|$$ 3$) chứng minh rằng đồ thị $({C_2})$ của hàm số $y = {\log _2}\left| {x + 1} \right|$ nhận đường thẳng $x = – 1$ làm trục đối xứng. Vẽ $({C_2})$

Đề: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} – 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$    $b)$ Qua điểm $A(1, 0)$  viết phương trình tiếp tuyến với đồ thị

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} - 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$    $b)$ Qua điểm $A(1, 0)$  viết phương trình tiếp tuyến với đồ thị Lời giải $1$. Ta có:\(\begin{array}{l}y = \frac{{{x^2} + {m^2}x + 2{m^2} - 5m + 3}}{x} … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} – 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$    $b)$ Qua điểm $A(1, 0)$  viết phương trình tiếp tuyến với đồ thị

Đề: Cho hàm số:                    $y = {x^3} – 3{x^2}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình tiếp tuyến với đồ thị của hàm số trên, biết rằng tiếp tuyến đó vuông góc với đường thẳng $y = \frac{x}{3}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:                    $y = {x^3} - 3{x^2}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình tiếp tuyến với đồ thị của hàm số trên, biết rằng tiếp tuyến đó vuông góc với đường thẳng $y = \frac{x}{3}$ Lời giải                                    Giải$1.$ Dành cho bạn đọc.$2.$ Phương trình đường thẳng vuông góc với đường thẳng … [Đọc thêm...] vềĐề: Cho hàm số:                    $y = {x^3} – 3{x^2}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình tiếp tuyến với đồ thị của hàm số trên, biết rằng tiếp tuyến đó vuông góc với đường thẳng $y = \frac{x}{3}$

Đề:   Tìm giá trị lớn nhất của hàm số: $y=[\frac{12x(x-a)}{x^2+36}]^\frac{3}{4}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:   Tìm giá trị lớn nhất của hàm số: $y=[\frac{12x(x-a)}{x^2+36}]^\frac{3}{4}$ Lời giải GiảiHàm số xác định khi $x(x-a) \geq 0$Đặt $z=\frac{12x(x-a)}{x^2+36}   (1)$ thì $y=\sqrt[4]{z^3}$ và $z \geq 0$Ta tìm $\max z$$z_0$ thuộc miền giá trị của hàm số $(1)$ khi và chỉ khi phương trình sau có nghiệm: $z_0=\frac{12x(x-a)}{x^2+36}$                               … [Đọc thêm...] vềĐề:   Tìm giá trị lớn nhất của hàm số: $y=[\frac{12x(x-a)}{x^2+36}]^\frac{3}{4}$