Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Cho hàm số: $y = \frac{{2x^2 + x + 1}}{{x + 1}}\,\,\,\,\,(1)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số $(1)$.$2$. Tìm những điểm trên trục tung sao cho từ đó ta có thể vẽ được hai tiếp tuyến tới đồ thị hàm số $(1)$ và hai tiếp tuyến đó vuông góc với nhau.$3$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: $A = \frac{{2\cos^2x + |\cos x| + 1}}{{|\cos x| + 1}}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số: $y = \frac{{2x^2 + x + 1}}{{x + 1}}\,\,\,\,\,(1)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số $(1)$.$2$. Tìm những điểm trên trục tung sao cho từ đó ta có thể vẽ được hai tiếp tuyến tới đồ thị hàm số $(1)$ và hai tiếp tuyến đó vuông góc với nhau.$3$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: $A = \frac{{2\cos^2x + |\cos x| + … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{2x^2 + x + 1}}{{x + 1}}\,\,\,\,\,(1)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số $(1)$.$2$. Tìm những điểm trên trục tung sao cho từ đó ta có thể vẽ được hai tiếp tuyến tới đồ thị hàm số $(1)$ và hai tiếp tuyến đó vuông góc với nhau.$3$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: $A = \frac{{2\cos^2x + |\cos x| + 1}}{{|\cos x| + 1}}$

Đề: Cho hàm số $y=4x^3-6x^2+1  (1)$. Viết phương trình tiếp tuyến của đồ thị hàm số $(1)$, biết rằng tiếp tuyến đó đi qua điểm $M(-1;-9)$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số $y=4x^3-6x^2+1  (1)$. Viết phương trình tiếp tuyến của đồ thị hàm số $(1)$, biết rằng tiếp tuyến đó đi qua điểm $M(-1;-9)$ Lời giải Gọi $(d)$ là đường thẳng đi qua điểm $M(-1;-9)$, đường thẳng $(d)$ có phương trình $y=kx+k-9$, đường thẳng $(d)$ trở thành tiếp tuyến của đồ thị hàm số $(1)$ khi và chỉ khi hệ phương trình sau có … [Đọc thêm...] vềĐề: Cho hàm số $y=4x^3-6x^2+1  (1)$. Viết phương trình tiếp tuyến của đồ thị hàm số $(1)$, biết rằng tiếp tuyến đó đi qua điểm $M(-1;-9)$

Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{\ln^2 x}{x}$ trên đoạn $[1;e^3]$.

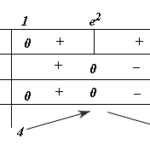
Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{\ln^2 x}{x}$ trên đoạn $[1;e^3]$. Lời giải Ta có : $y'=\frac{2\ln x.\frac{1}{x}x - \ln^2x}{x^2}=\frac{\ln x(2-\ln x)}{x^2}$.Từ đó có bảng biến thiên sau:Vậy $\mathop {\max  y }\limits_{ [1;e^3 ]}=y(e^2)=\frac{4}{e^2}\Leftrightarrow x=e^2$$\min y=\mathop {\min y }\limits_{ [1;e^3 ]}=\min (y(1);y(e^3))=\min … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{\ln^2 x}{x}$ trên đoạn $[1;e^3]$.

Đề: Gọi $D(m)$ là đường thẳng có phương trình $y=mx+1-m$(m là tham số). Chứng minh rằng khi $m$ thay đổi đường thẳng $D(m)$ xoay quanh một điểm cố định.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Gọi $D(m)$ là đường thẳng có phương trình $y=mx+1-m$(m là tham số). Chứng minh rằng khi $m$ thay đổi đường thẳng $D(m)$ xoay quanh một điểm cố định. Lời giải Gọi $(x_{0};y_{0})$ là một điểm mà họ đồ thị $D(m)$ luôn đi qua$\Leftrightarrow   y_{0}=mx_{0}+1-m$ đúng với $\forall m$$\Leftrightarrow   (y_{0} -1)+m(1-x_{0} )=0  \forall m $$\Leftrightarrow \left\{ … [Đọc thêm...] vềĐề: Gọi $D(m)$ là đường thẳng có phương trình $y=mx+1-m$(m là tham số). Chứng minh rằng khi $m$ thay đổi đường thẳng $D(m)$ xoay quanh một điểm cố định.

Đề: Cho hàm số: $y = x + 1 + \frac{1}{x – 1}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ đồ thị trên, hãy suy ra số nghiệm $x \in \left( {0 ; \frac{\pi }{2}} \right)$ của phương trình $1+\sin x+\cos x+\frac{1}{2}(\tan x + \cot x +\frac{1}{\sin x}+\frac{1}{\cos x})=m$tùy theo giá trị của tham số $m$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số: $y = x + 1 + \frac{1}{x - 1}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ đồ thị trên, hãy suy ra số nghiệm $x \in \left( {0 ; \frac{\pi }{2}} \right)$ của phương trình $1+\sin x+\cos x+\frac{1}{2}(\tan x + \cot x +\frac{1}{\sin x}+\frac{1}{\cos x})=m$tùy theo giá trị của tham số $m$ Lời giải $1)$     $y = x + 1 + \frac{1}{{x - 1}}$Hàm số xác … [Đọc thêm...] vềĐề: Cho hàm số: $y = x + 1 + \frac{1}{x – 1}$1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Từ đồ thị trên, hãy suy ra số nghiệm $x \in \left( {0 ; \frac{\pi }{2}} \right)$ của phương trình $1+\sin x+\cos x+\frac{1}{2}(\tan x + \cot x +\frac{1}{\sin x}+\frac{1}{\cos x})=m$tùy theo giá trị của tham số $m$

Đề: Xác định tính chẵn lẻ của các hàm số sau:a) $y=x(|x|-4)$b) $y=2x^{2}-3|x|+8$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Xác định tính chẵn lẻ của các hàm số sau:a) $y=x(|x|-4)$b) $y=2x^{2}-3|x|+8$ Lời giải Hàm số $y=f(x)$ với tập xác định $D$$f(x)$ là hàm chẵn nếu $x\in D$ thì $-x\in D$ và $f(x)=f(-x)$$f(x)$ là hàm lẻ nếu $x\in D$ thì $-x\in D$ và $f(x)=-f(-x)$a) Hàm số $y=x(|x|-4)$ Tập xác định $D=R$ * $x\in R$ thì $-x\in R$ * … [Đọc thêm...] vềĐề: Xác định tính chẵn lẻ của các hàm số sau:a) $y=x(|x|-4)$b) $y=2x^{2}-3|x|+8$

Đề: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:a) \(y=\cos (2x-1)\)b) \(y=2\sin x+\cos x\)

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:a) \(y=\cos (2x-1)\)b) \(y=2\sin x+\cos x\) Lời giải a) Đặt \(2x-1=t\), khi \(x\in R\) thì \(t\in R. \cos t\) có giá trị nhỏ nhất bằng -1 khi \(t=\left ( 2k+1 \right )\pi\) và có giá trị lớn nhất bằng 1 khi \(t=k2\pi\).Vậy giá trị nhỏ nhất của \(\cos (2x-1)\) là -1, giá trị lớn nhất của nó là 1.b) \(y=2\sin x+\cos … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:a) \(y=\cos (2x-1)\)b) \(y=2\sin x+\cos x\)

Đề: Cho hàm số $y = f(x) = \frac{x}{{1 + \left| x \right|}}$ $\left( {x \in R } \right)$Chứng minh hàm số đó có hàm số ngược $y = g(x)$ xác định trong khoảng $(-1, 1)$. Tìm hàm số $g(x)$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số $y = f(x) = \frac{x}{{1 + \left| x \right|}}$ $\left( {x \in R } \right)$Chứng minh hàm số đó có hàm số ngược $y = g(x)$ xác định trong khoảng $(-1, 1)$. Tìm hàm số $g(x)$ Lời giải $\left| y \right| = \frac{{\left| x \right|}}{{1 + \left| x \right|}} \Leftrightarrow  - 1 … [Đọc thêm...] vềĐề: Cho hàm số $y = f(x) = \frac{x}{{1 + \left| x \right|}}$ $\left( {x \in R } \right)$Chứng minh hàm số đó có hàm số ngược $y = g(x)$ xác định trong khoảng $(-1, 1)$. Tìm hàm số $g(x)$

Đề: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 – \left| x \right|}}$$    a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$  b)$ Tìm $g_0f$ và $f_0g.$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 - \left| x \right|}}$$    a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$  b)$ Tìm $g_0f$ và $f_0g.$ Lời giải $a)$ $f(x) = \frac{x}{{1 + \left| x \right|}}$ có miền xác định : $D = R$    $f( - x) =  - \frac{x}{{1 + \left| x \right|}} = -f(x) \Rightarrow … [Đọc thêm...] vềĐề: Cho các hàm số : $f(x) = \frac{x}{{1 + \left| x \right|}},g(x) = \frac{x}{{1 – \left| x \right|}}$$    a)$ Tìm miền xác định và miền giá trị của $f(x) $ và $g(x).$$  b)$ Tìm $g_0f$ và $f_0g.$

Đề: Cho hàm số $y=\frac{x^{2}+2x+3}{x^{2}+2}$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số $y=\frac{x^{2}+2x+3}{x^{2}+2}$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số. Lời giải +) Vì $x^{2}+2>0   \forall x\in R $ nên tập xác định của hàm số là: $R$Ta có: $y=\frac{x^{2}+2x+3}{x^{2}+2}=\frac{2\left ( x^{2}+2 \right )-\left ( x-1 \right )^{2}}{x^{2}+2}=2-\frac{\left ( x-1 \right )^{2}}{x^{2}+2}\leq 2, \forall x\in R$Hàm số đạt giá trị lớn … [Đọc thêm...] vềĐề: Cho hàm số $y=\frac{x^{2}+2x+3}{x^{2}+2}$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số.