![Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=frac{ln^2 x}{x}$ trên đoạn $[1;e^3]$. 1 ham so](https://booktoan.com/wp-content/uploads/2020/03/gt12.jpg)
Đề bài: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=\frac{\ln^2 x}{x}$ trên đoạn $[1;e^3]$.
Lời giải
Ta có : $y’=\frac{2\ln x.\frac{1}{x}x – \ln^2x}{x^2}=\frac{\ln x(2-\ln x)}{x^2}$.
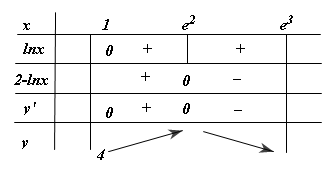
Từ đó có bảng biến thiên sau:![Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=frac{ln^2 x}{x}$ trên đoạn $[1;e^3]$. 2 Đề: Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y=frac{ln^2 x}{x}$ trên đoạn $[1;e^3]$. 1](https://booktoan.com/wp-content/uploads/2021/07/unnamed-file-34.png)
Vậy $\mathop {\max y }\limits_{ [1;e^3 ]}=y(e^2)=\frac{4}{e^2}\Leftrightarrow x=e^2$
$\min y=\mathop {\min y }\limits_{ [1;e^3 ]}=\min (y(1);y(e^3))=\min (0;\frac{9}{e^3})=0\Leftrightarrow x=1$.
