Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Cho hàm số $y=x^{3}-3x^{2}+1$.Chứng minh rằng đồ thị hàm số nhận điểm $I(1;-1)$ làm tâm đối xứng.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

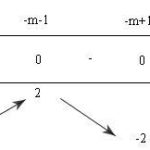
Đề bài: Cho hàm số $y=x^{3}-3x^{2}+1$.Chứng minh rằng đồ thị hàm số nhận điểm $I(1;-1)$ làm tâm đối xứng. Lời giải Với phép biến đổi tọa độ:$\begin{cases} X=x-1 \\Y=y+1\end{cases} \Leftrightarrow \begin{cases} x=X+1 \\y=Y-1 \end{cases} $Khi đó hàm số có dạng:$Y-1=(X+1)^{3}-3(X+1)^{2}+1 \Leftrightarrow Y=X^{3}-3X$ (1)Hàm số (1) là hàm số lẻ.Vậy,đồ thị hàm số nhận điểm … [Đọc thêm...] vềĐề: Cho hàm số $y=x^{3}-3x^{2}+1$.Chứng minh rằng đồ thị hàm số nhận điểm $I(1;-1)$ làm tâm đối xứng.

Đề: Cho hàm số:  $y = 4x^3 + mx$a) Tùy theo các giá trị của $a$, hãy xét sự biến thiên của hàm sốb) Xác định $m$ để $\left| y \right| \le 1$ khi $\left| x \right| \le 1$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:  $y = 4x^3 + mx$a) Tùy theo các giá trị của $a$, hãy xét sự biến thiên của hàm sốb) Xác định $m$ để $\left| y \right| \le 1$ khi $\left| x \right| \le 1$ Lời giải a) Hàm số được xác định với mọi $x$, có đạo hàm $y' = 12{x^2} + m$•    Với $m > 0$ ta có $y' \ge 0$ với mọi $x$, suy ra $y$ luôn đồng biến với mọi $x$.•    Với $m Ta có … [Đọc thêm...] vềĐề: Cho hàm số:  $y = 4x^3 + mx$a) Tùy theo các giá trị của $a$, hãy xét sự biến thiên của hàm sốb) Xác định $m$ để $\left| y \right| \le 1$ khi $\left| x \right| \le 1$

Đề: Tìm đạo hàm của các hàm số:a) \(y=\sqrt{x^{3}-2x^{2}+1}\)b) \(y=\frac{2x+1}{\sqrt{x^{2}+1}}\).

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm đạo hàm của các hàm số:a) \(y=\sqrt{x^{3}-2x^{2}+1}\)b) \(y=\frac{2x+1}{\sqrt{x^{2}+1}}\). Lời giải a) \(y'=[\sqrt{u}]'=\frac{u'}{2\sqrt{u}}\) với \(u=x^{3}-2x^{2}+1\)\(y'=\frac{[x^{3}-2x^{2}+1]'}{2\sqrt{x^{3}-2x^{2}+1}}=\frac{3x^{2}-4x}{2\sqrt{x^{3}-2x^{2}+1}}\).b) … [Đọc thêm...] vềĐề: Tìm đạo hàm của các hàm số:a) \(y=\sqrt{x^{3}-2x^{2}+1}\)b) \(y=\frac{2x+1}{\sqrt{x^{2}+1}}\).

Đề: Cho hàm số: $y = x^3 + 3mx^2 + 3(m^2 – 1)x + m^3 – 3m\,\,\,\,(C)$    $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 0.$$2.$ Chứng minh rằng với mọi $m$ hàm số đã cho luôn luôn có cực đại và cực tiểu, đồng thời chứng minh khi $m$ thay đổi, các điểm cực đại và cực tiểu của đồ thị hàm số luôn luôn chạy trên hai đường thẳng cố định.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số: $y = x^3 + 3mx^2 + 3(m^2 - 1)x + m^3 - 3m\,\,\,\,(C)$    $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 0.$$2.$ Chứng minh rằng với mọi $m$ hàm số đã cho luôn luôn có cực đại và cực tiểu, đồng thời chứng minh khi $m$ thay đổi, các điểm cực đại và cực tiểu của đồ thị hàm số luôn luôn chạy trên hai đường thẳng cố định. Lời giải $1.$ Xin dành … [Đọc thêm...] vềĐề: Cho hàm số: $y = x^3 + 3mx^2 + 3(m^2 – 1)x + m^3 – 3m\,\,\,\,(C)$    $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 0.$$2.$ Chứng minh rằng với mọi $m$ hàm số đã cho luôn luôn có cực đại và cực tiểu, đồng thời chứng minh khi $m$ thay đổi, các điểm cực đại và cực tiểu của đồ thị hàm số luôn luôn chạy trên hai đường thẳng cố định.

Đề: Cho $A = R/\left\{ 1 \right\}$ và ánh xạ \(f:A \to A\) xác định như sau:$f:x \to \frac{x + 1}{x – 1}$ a.    Chứng minh rằng $f$ là một song ánh. b.    Xác định ánh xại ngược $f^{ – 1}$. Có nhận xét gì  ?

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho $A = R/\left\{ 1 \right\}$ và ánh xạ \(f:A \to A\) xác định như sau:$f:x \to \frac{x + 1}{x - 1}$ a.    Chứng minh rằng $f$ là một song ánh. b.    Xác định ánh xại ngược $f^{ - 1}$. Có nhận xét gì  ? Lời giải a.    Ta có : $\begin{array}{l}\left( {\forall {y_0} \in A,f\left( x \right) = {y_0}} \right) \Leftrightarrow \frac{{x + 1}}{{x - 1}} = … [Đọc thêm...] vềĐề: Cho $A = R/\left\{ 1 \right\}$ và ánh xạ \(f:A \to A\) xác định như sau:$f:x \to \frac{x + 1}{x – 1}$ a.    Chứng minh rằng $f$ là một song ánh. b.    Xác định ánh xại ngược $f^{ – 1}$. Có nhận xét gì  ?

Đề: Cho hàm số:  $y = \frac{{{x^2} – x + 1}}{{x – 1}}$1)    Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2)    Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3)    Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:  $y = \frac{{{x^2} - x + 1}}{{x - 1}}$1)    Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2)    Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3)    Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$ Lời giải $1)$    Dành cho bạn đọc.$2)$    Tìm $A(0, b)$ là một điểm trên trục $Oy$ mà tiếp … [Đọc thêm...] vềĐề: Cho hàm số:  $y = \frac{{{x^2} – x + 1}}{{x – 1}}$1)    Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2)    Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3)    Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$

Đề: Xét tính chẵn, lẻ của các hàm số sau :$a) f(x) = sinx + cosx$            $b) f(x) = 0$$c) f(x) = 2xsinx $                      $d) f(x) = 2$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Xét tính chẵn, lẻ của các hàm số sau :$a) f(x) = sinx + cosx$            $b) f(x) = 0$$c) f(x) = 2xsinx $                      $d) f(x) = 2$ Lời giải $a) f(x) = sinx + cosx$Miền xác định : $D = R$ là tập đối xứng qua điểm x$ = 0.$$\forall x \in D, -x \in D$Mà $f\left( {\frac{\pi }{4}} \right) = \sqrt 2 $,  $f\left( { - \frac{\pi }{4}} \right) = 0$$f\left( … [Đọc thêm...] vềĐề: Xét tính chẵn, lẻ của các hàm số sau :$a) f(x) = sinx + cosx$            $b) f(x) = 0$$c) f(x) = 2xsinx $                      $d) f(x) = 2$

Đề: Cho hàm số:  $y = x + \sqrt {4{x^2} + 2x + 1} $.1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Xác định tất cả các điểm trên trục tung, sao cho từ mỗi điểm ấy ta có thể vẽ được ít nhất  một tiếp tuyến đến đồ thị

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:  $y = x + \sqrt {4{x^2} + 2x + 1} $.1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Xác định tất cả các điểm trên trục tung, sao cho từ mỗi điểm ấy ta có thể vẽ được ít nhất  một tiếp tuyến đến đồ thị Lời giải $1)$ $4{x^2} + 2x + 1 = 3{x^2} + {(x + 1)^2} > 0,{\rm{ }}\forall {\rm{x}}$ nên hàm số xác định với mọi $x$. Tiệm cận xiên của đồ thị (về phía … [Đọc thêm...] vềĐề: Cho hàm số:  $y = x + \sqrt {4{x^2} + 2x + 1} $.1) Khảo sát sự biến thiên và vẽ đồ thị hàm số.2) Xác định tất cả các điểm trên trục tung, sao cho từ mỗi điểm ấy ta có thể vẽ được ít nhất  một tiếp tuyến đến đồ thị

Đề: Tìm GTLN của hàm số: $f(x) = \left| {x^3 + 3x^2 – 72x + 90} \right|$ trên đoạn $[-5;5]$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm GTLN của hàm số: $f(x) = \left| {x^3 + 3x^2 - 72x + 90} \right|$ trên đoạn $[-5;5]$ Lời giải Xét hàm số $g(x)=x^3+3x^2-72x+90$ liên tục trên $[-5,5]$ có $g^/(x)=3x^2+6x-72$ triệt tiêu tại $x_1=4,x_2=-6.$ Ta thấy $x_1\in [-5,5]$,$x_2\notin [-5,5]$.Tính $g(-5)=400,g(5)=-70,g(4)=-86.$Do đó $max  g(x)=400,x\in [-5,5].Min  g(x)=-86,x_2\in [-5,5]$Vì vậy … [Đọc thêm...] vềĐề: Tìm GTLN của hàm số: $f(x) = \left| {x^3 + 3x^2 – 72x + 90} \right|$ trên đoạn $[-5;5]$

Đề: Cho hàm số: $y = f(x) = \frac{x^2 – 2mx + m + 2}{x – m}$$1.$ Với giá trị nào của $m$ thì hàm số đồng biến với mọi $x > 1.$$2.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$3.$ Biện luận theo $a$ số nghiệm của phương trình: $\frac{{x^2 – 2|x| + 3}}{|x| – 1} = a$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số: $y = f(x) = \frac{x^2 - 2mx + m + 2}{x - m}$$1.$ Với giá trị nào của $m$ thì hàm số đồng biến với mọi $x > 1.$$2.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$3.$ Biện luận theo $a$ số nghiệm của phương trình: $\frac{{x^2 - 2|x| + 3}}{|x| - 1} = a$ Lời giải $1.$ $y^/=\frac{x^2-2mx+2m^2-m-2}{(x-m)^2} $ Hàm số đồng biến … [Đọc thêm...] vềĐề: Cho hàm số: $y = f(x) = \frac{x^2 – 2mx + m + 2}{x – m}$$1.$ Với giá trị nào của $m$ thì hàm số đồng biến với mọi $x > 1.$$2.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$3.$ Biện luận theo $a$ số nghiệm của phương trình: $\frac{{x^2 – 2|x| + 3}}{|x| – 1} = a$