Đề bài: Cho hàm số $f(x)=\sqrt{x}$. Tính $f^{'}(3)$ Lời giải $f(x)=\sqrt{x} \Rightarrow f^{'}(x)=\frac{1}{2\sqrt{x}}$Vậy $f^{'}(3)=\frac{1}{2\sqrt{3}}$ … [Đọc thêm...] vềĐề: Cho hàm số $f(x)=\sqrt{x}$. Tính $f^{'}(3)$
Kết quả tìm kiếm cho: ty so
Đề: Tính số gia của hàm số \(y=x^{3}+1\) tại điểm đã cho cùng với số gia của đối số tương ứng.a) \(x_{0}=1, \Delta x=0,1\)b) \(x_{0}=1,5,\Delta x=0,3\).
Đề bài: Tính số gia của hàm số \(y=x^{3}+1\) tại điểm đã cho cùng với số gia của đối số tương ứng.a) \(x_{0}=1, \Delta x=0,1\)b) \(x_{0}=1,5,\Delta x=0,3\). Lời giải a) \(\Delta y=f(1+0,1)-f(1)=0,331\)b) \( \Delta y=f(1,5+0,3)-f(1,5)=5,832\). … [Đọc thêm...] vềĐề: Tính số gia của hàm số \(y=x^{3}+1\) tại điểm đã cho cùng với số gia của đối số tương ứng.a) \(x_{0}=1, \Delta x=0,1\)b) \(x_{0}=1,5,\Delta x=0,3\).
Đề: Tìm giá trị nhỏ nhất của biểu thức: $\frac{a^2}{1-a}+\frac{b^2}{1-b}+\frac{1}{a+b}+a+b$.trong đó, $a,b$ là hai số thực dương thỏa mãn điều kiện $a+b
Đề bài: Tìm giá trị nhỏ nhất của biểu thức: $\frac{a^2}{1-a}+\frac{b^2}{1-b}+\frac{1}{a+b}+a+b$.trong đó, $a,b$ là hai số thực dương thỏa mãn điều kiện $a+b Lời giải Đặt $M=\frac{a^2}{1-a}+\frac{b^2}{1-b}+\frac{1}{a+b}+a+b$ $=\frac{a^2}{1-a}+1+a+\frac{b^2}{1-b}+1+b+\frac{1}{a+b}-2$ $=\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{a+b}-2$.Áp dụng bất đẳng … [Đọc thêm...] vềĐề: Tìm giá trị nhỏ nhất của biểu thức: $\frac{a^2}{1-a}+\frac{b^2}{1-b}+\frac{1}{a+b}+a+b$.trong đó, $a,b$ là hai số thực dương thỏa mãn điều kiện $a+b
Đề: Cho hàm số: $y = kx^4+ (k – 1)x^2 + (1 – 2k)$$1$. Xác định các giá trị của tham số $k$ để đồ thị hàm số chỉ có một điểm cực trị.$2$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $k = \frac{1}{2}$$3$. Viết phương trình các tiếp tuyến của đồ thị ở phần $2)$ đi qua gốc tọa độ.
Đề bài: Cho hàm số: $y = kx^4+ (k - 1)x^2 + (1 - 2k)$$1$. Xác định các giá trị của tham số $k$ để đồ thị hàm số chỉ có một điểm cực trị.$2$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $k = \frac{1}{2}$$3$. Viết phương trình các tiếp tuyến của đồ thị ở phần $2)$ đi qua gốc tọa độ. Lời giải $1.$ $y^/=2x(2kx^2+k-1) f(x)=2kx^2+k-1$$y$ chỉ có $1$ cực trị … [Đọc thêm...] vềĐề: Cho hàm số: $y = kx^4+ (k – 1)x^2 + (1 – 2k)$$1$. Xác định các giá trị của tham số $k$ để đồ thị hàm số chỉ có một điểm cực trị.$2$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $k = \frac{1}{2}$$3$. Viết phương trình các tiếp tuyến của đồ thị ở phần $2)$ đi qua gốc tọa độ.
Đề: Xét sự biến thiên của các hàm sốa) $y=\frac{x}{x-1} $; b) $y=-\frac{1}{x}$; c) $y=\frac{1}{x^2}$.
Đề bài: Xét sự biến thiên của các hàm sốa) $y=\frac{x}{x-1} $; b) $y=-\frac{1}{x}$; c) $y=\frac{1}{x^2}$. Lời giải a) Tập xác định $D=(-\infty ,1)\cup (1,+\infty ).$ *, Lấy $x_1,x_2 $\frac{f(x_{2})-f(x_{1})}{x_{2}-x_{1}} … [Đọc thêm...] vềĐề: Xét sự biến thiên của các hàm sốa) $y=\frac{x}{x-1} $; b) $y=-\frac{1}{x}$; c) $y=\frac{1}{x^2}$.
Đề: Cho hàm số $ y = \frac{2x – 1}{x + 1} (1)$. Tìm điểm $M$ thuộc đồ thị $(C)$ để tiếp tuyến của $(C)$ tại $M$ với đường thẳng đi qua $M$ và giao điểm hai đường tiệm cận có tích hệ số góc bằng $-9$.
Đề bài: Cho hàm số $ y = \frac{2x - 1}{x + 1} (1)$. Tìm điểm $M$ thuộc đồ thị $(C)$ để tiếp tuyến của $(C)$ tại $M$ với đường thẳng đi qua $M$ và giao điểm hai đường tiệm cận có tích hệ số góc bằng $-9$. Lời giải +) Ta có I(- 1; 2). Gọi $ M \in (C) \Rightarrow M({x_0};2 - \frac{3}{{{x_0} + 1}}) \Rightarrow {k_{IM}} = \frac{{{y_M} - {y_I}}}{{{x_M} - {x_I}}} = \frac{{ - … [Đọc thêm...] vềĐề: Cho hàm số $ y = \frac{2x – 1}{x + 1} (1)$. Tìm điểm $M$ thuộc đồ thị $(C)$ để tiếp tuyến của $(C)$ tại $M$ với đường thẳng đi qua $M$ và giao điểm hai đường tiệm cận có tích hệ số góc bằng $-9$.
Đề: Cho $f:[0,1]\to [0,\to \infty ]$ liên tục.Đặt: $I_{n}=\int\limits^{1}_{0} f^{n}(x)dx,n\geq 3$Chứng minh rằng: $I^{2}_{n-1}\leq I_{n}.I_{n-2}$
Đề bài: Cho $f:[0,1]\to [0,\to \infty ]$ liên tục.Đặt: $I_{n}=\int\limits^{1}_{0} f^{n}(x)dx,n\geq 3$Chứng minh rằng: $I^{2}_{n-1}\leq I_{n}.I_{n-2}$ Lời giải Ta có: $I^{2}_{n-1}=[\int\limits^{1}_{0} f^{\frac{n}{2}}(x).f^{\frac{n-2}{2}}(x)dx]^{2}$$\leq \int\limits^{1}_{0} f^{n}(x)dx\int\limits^{1}_{0} f^{n-2}(x)dx=I_{n}.I_{n-2}$$\Rightarrow$ (ĐPCM) … [Đọc thêm...] vềĐề: Cho $f:[0,1]\to [0,\to \infty ]$ liên tục.Đặt: $I_{n}=\int\limits^{1}_{0} f^{n}(x)dx,n\geq 3$Chứng minh rằng: $I^{2}_{n-1}\leq I_{n}.I_{n-2}$
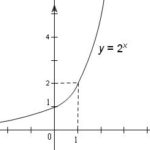
Đề: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$
Đề bài: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$ Lời giải $1)$.. Lập bảng biến thiên và vẽ đồ thị ($C$) của hàm số $y = {2^x}$ Đồ thị $({C^,})$của hàm số $y = {\left( {\frac{1}{2}} \right)^x}$ là đường đối xứng của ($C$) qua trục tung $Oy.$$2)$ Đồ thị $({C_1})$ của hàm số $y … [Đọc thêm...] vềĐề: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$
Đề: Xét tính liên tục của hàm số: $f(x)=\begin{cases} x^{3}+x+1;x\geq 1\\ 2x+4 ;x
Đề bài: Xét tính liên tục của hàm số: $f(x)=\begin{cases} x^{3}+x+1;x\geq 1\\ 2x+4 ;x Lời giải Dễ thấy ngay, hàm số liên tục trên các khoảng $(-\infty;3), (3;5), (5;+\infty)$.Chỉ cần xét tính liên tục của $f(x)$ tại điểm $x=3,x=5$. $\mathop {\lim }\limits_{x \to 3^-}f(x)=1; \mathop {\lim }\limits_{x \to 3^+}f(x)=3a+b ; f(3)=1 $Nên … [Đọc thêm...] vềĐề: Xét tính liên tục của hàm số: $f(x)=\begin{cases} x^{3}+x+1;x\geq 1\\ 2x+4 ;x
Đề: Tính đạo hàm số cấp $n$ của hàm số:a) $y=\ln x$b) $y=\ln(x^2+x-2).$
Đề bài: Tính đạo hàm số cấp $n$ của hàm số:a) $y=\ln x$b) $y=\ln(x^2+x-2).$ Lời giải a) Ta có $y'=(\ln x)'=\frac{1}{x}, y''=-\frac{1}{x^2}, y'''=\frac{1.2}{x^3}, y^{(4)}=-\frac{1.2.3}{x^4} $bằng phương pháp quy nạp, ta chứng minh được:$y^{(n)}=(-1)^{n+1.\frac{(n-1)!}{x^n} }, n\in \mathbb{Z} ^*$b) Điều kiện $x1$ Với điều kiện trên thì $x^2+x-2=(x-1)(x+2)>0$, do … [Đọc thêm...] vềĐề: Tính đạo hàm số cấp $n$ của hàm số:a) $y=\ln x$b) $y=\ln(x^2+x-2).$