Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số  \(y = \frac{{{x^2}}}{{x – 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\).

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số  \(y = \frac{{{x^2}}}{{x - 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\). Lời giải $1$. Bạn đọc tự giải:$2$. Đường thẳng $y = 4$ tiếp xúc với $(C)$ tại điểm $(2, 4)$. Các điểm cần tìm là các giao … [Đọc thêm...] vềĐề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số  \(y = \frac{{{x^2}}}{{x – 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\).

Đề: Cho hàm số \(y = {x^3} – 3{x^2} + 3mx + 3m + 4\,\,\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =1$$2$. Hãy xác định giá trị của $m$ để đường cong \(\left( {{C_m}} \right)\) nhân điểm $I(1, 2)$ làm điểm uốn$3$. Với những giá trị nào của $m$ thì đường cong \(\left( {{C_m}} \right)\) tiếp xúc với trục hoành.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số \(y = {x^3} - 3{x^2} + 3mx + 3m + 4\,\,\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =1$$2$. Hãy xác định giá trị của $m$ để đường cong \(\left( {{C_m}} \right)\) nhân điểm $I(1, 2)$ làm điểm uốn$3$. Với những giá trị nào của $m$ thì đường cong \(\left( {{C_m}} \right)\) tiếp xúc với trục hoành. Lời giải $1$. Bạn đọc tự … [Đọc thêm...] vềĐề: Cho hàm số \(y = {x^3} – 3{x^2} + 3mx + 3m + 4\,\,\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =1$$2$. Hãy xác định giá trị của $m$ để đường cong \(\left( {{C_m}} \right)\) nhân điểm $I(1, 2)$ làm điểm uốn$3$. Với những giá trị nào của $m$ thì đường cong \(\left( {{C_m}} \right)\) tiếp xúc với trục hoành.

Đề: Cho $x, y$ là hai số thay đổi thỏa mãn điều kiện:  $0 \le x \le 3,0 \le y \le 4$.Tìm giá trị lớn nhất của biểu thức:  $A = (3 – x)(4 – y)(2x + 3y)$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho $x, y$ là hai số thay đổi thỏa mãn điều kiện:  $0 \le x \le 3,0 \le y \le 4$.Tìm giá trị lớn nhất của biểu thức:  $A = (3 - x)(4 - y)(2x + 3y)$ Lời giải Ta có:  $6A = (6 - 2x)(12 - 3y)(2x + 3y)$Theo giả thiết ta có $6 - 2x \ge 0,{\rm{ 12}} - 3y \ge 0,{\rm{ 2x}} + 3y \ge 0$Do đó áp dụng bất đẳng thức Côsi cho ba số không âm ta được:$6A \le {\left[ {\frac{{(6 - … [Đọc thêm...] vềĐề: Cho $x, y$ là hai số thay đổi thỏa mãn điều kiện:  $0 \le x \le 3,0 \le y \le 4$.Tìm giá trị lớn nhất của biểu thức:  $A = (3 – x)(4 – y)(2x + 3y)$

Đề: a) Tìm các khoảng đơn điệu của hàm số $y=x \ln^2 x.$b) Tìm điểm cực trị của hàm số $y=f(x)=x^2\ln x.$

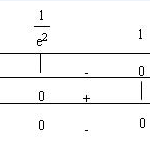
Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: a) Tìm các khoảng đơn điệu của hàm số $y=x \ln^2 x.$b) Tìm điểm cực trị của hàm số $y=f(x)=x^2\ln x.$ Lời giải a) Hàm số $y=x \ln^2 x$ có tập xác định $D=(0;+\infty)$ Ta có $y'=\ln x (\ln x+2)$. Do đó $ y'=0\Leftrightarrow \left[ \begin{array}{l}\ln x=0\\\ln x=-2\end{array} \right.\Leftrightarrow \left[ \begin{array}{l}x=1\\x=\frac{1}{e^2} \end{array} \right.$Vậy … [Đọc thêm...] vềĐề: a) Tìm các khoảng đơn điệu của hàm số $y=x \ln^2 x.$b) Tìm điểm cực trị của hàm số $y=f(x)=x^2\ln x.$

Đề: Tính đạo hàm các hàm số sau đây:a) $y=\sin 3x-\cos3x$ b) $y=\frac {x}{\sin x}$ c) $y=\sin ^32x$ d) $y= \cos \frac{1}{x}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tính đạo hàm các hàm số sau đây:a) $y=\sin 3x-\cos3x$ b) $y=\frac {x}{\sin x}$ c) $y=\sin ^32x$ d) $y= \cos \frac{1}{x}$ Lời giải Ta có:a) $y'=(\sin3x)'-(\cos3x)'=3\cos3x+3\sin3x$.b) $y'=\frac{\sin x(x)'-(\sin x)'.x}{\sin^2x}=\frac{\sin x -x\cos x}{\sin^2x}$ .c) $y'=3\sin^22x(\sin2x)'=6\sin^22x\cos2x$ .d) $y'= … [Đọc thêm...] vềĐề: Tính đạo hàm các hàm số sau đây:a) $y=\sin 3x-\cos3x$ b) $y=\frac {x}{\sin x}$ c) $y=\sin ^32x$ d) $y= \cos \frac{1}{x}$

Đề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x - 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 - 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$ Lời giải        1. Khảo sát , đồ thị (xin dành cho bạn đọc).         Từ đồ thị hàm số: $y = 3x - 4{x^3}$ta suy ra đồ thị hàm số $y = |x|\left( {3 - 4{x^2}} … [Đọc thêm...] vềĐề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$

Đề: Tìm tập xác định của hàm số:$y = {2^{\sqrt {\left| {X – 3} \right| – \left| {8 – X} \right|} }} + {\sqrt {\frac{{ – {{\log }_{0,3}}(X – 1)}}{{\sqrt {{X^2} – 2X – 8} }}} _{}}$ĐH Y Hà Nội 1997

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm tập xác định của hàm số:$y = {2^{\sqrt {\left| {X - 3} \right| - \left| {8 - X} \right|} }} + {\sqrt {\frac{{ - {{\log }_{0,3}}(X - 1)}}{{\sqrt {{X^2} - 2X - 8} }}} _{}}$ĐH Y Hà Nội 1997 Lời giải … [Đọc thêm...] vềĐề: Tìm tập xác định của hàm số:$y = {2^{\sqrt {\left| {X – 3} \right| – \left| {8 – X} \right|} }} + {\sqrt {\frac{{ – {{\log }_{0,3}}(X – 1)}}{{\sqrt {{X^2} – 2X – 8} }}} _{}}$ĐH Y Hà Nội 1997

Đề: Cho hàm số  $ y_k=\frac{2k\cos x+k+1}{\cos x+\sin x+2}$a) Tìm giá trị lớn nhất và giá trị nhỏ nhất với $y_1$ ( ứng với $k=1$)b) Tìm $k$ để giá trị lớn nhất  của $y_k$ là nhỏ nhất.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số  $ y_k=\frac{2k\cos x+k+1}{\cos x+\sin x+2}$a) Tìm giá trị lớn nhất và giá trị nhỏ nhất với $y_1$ ( ứng với $k=1$)b) Tìm $k$ để giá trị lớn nhất  của $y_k$ là nhỏ nhất. Lời giải Miền xác định :  $ D=R$ ( vì $ \cos x+\sin x+2=\sqrt{2}\left ( \sqrt{2}+\sin (x+\frac{\pi}{4}) \right )>0, \forall x \in R$)Khi đó:  $(y_k-2k)\cos x+y_k\sin 2x=k+1-2y_k$Điều kiện … [Đọc thêm...] vềĐề: Cho hàm số  $ y_k=\frac{2k\cos x+k+1}{\cos x+\sin x+2}$a) Tìm giá trị lớn nhất và giá trị nhỏ nhất với $y_1$ ( ứng với $k=1$)b) Tìm $k$ để giá trị lớn nhất  của $y_k$ là nhỏ nhất.

Đề:  Cho hàm số   $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1)    Với giá trị nào của $m$ thì hàm số có cực trị?2)    Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3)    Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:  Cho hàm số   $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1)    Với giá trị nào của $m$ thì hàm số có cực trị?2)    Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3)    Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$ Lời giải $1)$    Ta có $y = x + 2{m^2} - 1 + \frac{{1 - {m^2}}}{{x + 1}}$, do đó$y' = 1 - \frac{{1 - … [Đọc thêm...] vềĐề:  Cho hàm số   $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1)    Với giá trị nào của $m$ thì hàm số có cực trị?2)    Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3)    Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$

Đề: Cho hàm số \(y = \frac{{{x^2} – x + 1}}{{x – 1}}\)$1$. Khảo sát hàm số đã cho$2$. Xác định điểm \(A\left( {{x_1},{y_1}} \right)\) thuộc đồ thị của hàm số trên sao cho khoảng cách từ $A$ đến giao điểm của hai tiệm cận là nhỏ nhất.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)$1$. Khảo sát hàm số đã cho$2$. Xác định điểm \(A\left( {{x_1},{y_1}} \right)\) thuộc đồ thị của hàm số trên sao cho khoảng cách từ $A$ đến giao điểm của hai tiệm cận là nhỏ nhất. Lời giải $1$. Bạn đọc tự giải$2$. Giao điểm hai tiệm cận là $E (1, 1)$. Xét điểm \(A\left( {{x_1},{y_1}} \right)\) với \({x_1} > 1\)$A$ … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} – x + 1}}{{x – 1}}\)$1$. Khảo sát hàm số đã cho$2$. Xác định điểm \(A\left( {{x_1},{y_1}} \right)\) thuộc đồ thị của hàm số trên sao cho khoảng cách từ $A$ đến giao điểm của hai tiệm cận là nhỏ nhất.