Đề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$

Đề bài: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$

Lời giải

     
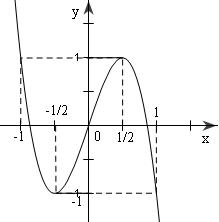
  1. Khảo sát , đồ thị (xin dành cho bạn đọc). 
  
      

Từ đồ thị hàm số: $y = 3x – 4{x^3}$ta suy ra đồ thị hàm số $y = |x|\left( {3 – 4{x^2}} \right)$
Hàm số chẵn, đồ thị nhận trục tung $Oy$ làm trục đối xứng. Khi $x \ge 0$, $y = 3x – 4{x^3}$trùng với đồ thị đã cho ở trên.
$2.$ Đường thẳng đi qua $A(1;3)$ hệ số góc $k$ có phương trình: $y = k(x – 1) + 3$. Đường thẳng này sẽ là một tiếp tuyến của đồ thị hàm số $y = 3x – 4{x^3}$khi và chỉ khi hệ sau có nghiệm:
$\left\{ \begin{array}{l}
k(x – 1) + 3 = 3x – 4{x^3}\\
k = 3 – 12{x^2}
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = \frac{3}{2}
\end{array} \right.$
+ Với $x = 0  \Rightarrow k = 3$ ta có tiếp tuyến $y = 3x$
+ Với $x = 3/2  \Rightarrow k = -24$ ta có tiếp tuyến $y = -24x + 27.$