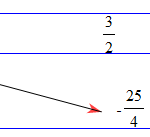
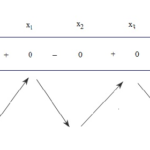
Đề bài: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$ Lời giải Giải* Tập xác định $R$* Sự biến thiên: Ta có: $a=1>0, -\frac{b}{2a}=\frac{3}{2}, -\frac{\Delta}{4a}=-\frac{25}{4}$. Vậy đồ thị hàm số $y=x^2-3x-4$ là parabol có đỉnh $I(\frac{3}{2};-\frac{25}{4})$, nhận đường thẳng $x=\frac{3}{2}$ làm tâm đối xứng và bề lõm hướng lên trên. Suy ra: Hàm số nghịch biến trên khoảng … [Đọc thêm...] vềĐề: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$
Kết quả tìm kiếm cho: ty so
Đề: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x – 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau
Đề bài: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x - 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau Lời giải $1$. Bạn đọc tự giải$2$. Xét \(A\left( {0,a} \right)\) trên $Oy$. Đường thẳng qua $A$ với hệ số góc $k$ có phương trình \(y = kx + … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x – 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau
Đề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y=\frac{\cos x+2\sin x+3}{2\cos x-\sin x+4}$, với $-\pi
Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y=\frac{\cos x+2\sin x+3}{2\cos x-\sin x+4}$, với $-\pi Lời giải Biến đổi hàm số về dạng: $(2y-1)\cos x-(y+2)\sin x=3-4y (1)$Phương trình $(1)$ có nghiệm khi: $(2y-1)^2+(y+2)^2\geq (3-4y)^2\Leftrightarrow 11y^2-24y+4\leq 0\Leftrightarrow \frac{2}{11}\leq y \leq 2$.Vậy, ta có: - … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y=\frac{\cos x+2\sin x+3}{2\cos x-\sin x+4}$, với $-\pi
Đề: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị.
Đề bài: Cho hàm số \(y = - {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị. Lời giải $1$. Bạn đọc tự giải.$2$. Với \(m = 1\), có \(y = f\left( … [Đọc thêm...] vềĐề: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị.
Đề: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y – x + 6 = 0$
Đề bài: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y - x + 6 = 0$ Lời giải $1)$ Viết lại biểu … [Đọc thêm...] vềĐề: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y – x + 6 = 0$
Đề: Cho \(a>0,x,y\) là \(2\) số dương thỏa \(a(x+y)\sqrt{3}=xy\)Tìm giá trị nhỏ nhất của \(xy\) và của \(x^{2}+y^{2}-xy\).
Đề bài: Cho \(a>0,x,y\) là \(2\) số dương thỏa \(a(x+y)\sqrt{3}=xy\)Tìm giá trị nhỏ nhất của \(xy\) và của \(x^{2}+y^{2}-xy\). Lời giải Từ giả thiết: \(a(x+y)\sqrt{3}=xy \Rightarrow xy=a\sqrt{3}(x+y)\geq a\sqrt{3} 2\sqrt{xy}\)\(\Rightarrow xy\geq 12a^{2}\)Vậy \(xy\) nhỏ nhất là \(12a^{2}\) khi \(x=y=2a\sqrt{3}\) \(x^{2}+y^{2}-xy\geq 2xy-xy=xy\geq 12a^{2}\)\(\Rightarrow … [Đọc thêm...] vềĐề: Cho \(a>0,x,y\) là \(2\) số dương thỏa \(a(x+y)\sqrt{3}=xy\)Tìm giá trị nhỏ nhất của \(xy\) và của \(x^{2}+y^{2}-xy\).
Đề: Cho hàm số \(y = \frac{{{x^2} – x – 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} – \left( {1 + m} \right)|x| – m – 1 = 0\)
Đề bài: Cho hàm số \(y = \frac{{{x^2} - x - 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} - \left( {1 + m} \right)|x| - m - 1 = 0\) Lời … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} – x – 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} – \left( {1 + m} \right)|x| – m – 1 = 0\)
Đề: Cho hàm số $y = f(x) = mx^3 + 3mx^2-(m – 1)x – 1 $ với $m$ là tham số.$1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $y = f(x)$ không có cực trị.
Đề bài: Cho hàm số $y = f(x) = mx^3 + 3mx^2-(m - 1)x - 1 $ với $m$ là tham số.$1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $y = f(x)$ không có cực trị. Lời giải $1.$ Xin dành cho bạn đọc.$2.$$\begin{array}{l}y = f(x) = m{x^3} + 3m{x^2} - (m - 1)x - 1\\\,f'(x) = 3m{x^2} + 6mx - (m - 1)\\*\,m\, = \,0 \Rightarrow … [Đọc thêm...] vềĐề: Cho hàm số $y = f(x) = mx^3 + 3mx^2-(m – 1)x – 1 $ với $m$ là tham số.$1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m = 1.$$2$. Tìm tất cả các giá trị của $m$ để hàm số $y = f(x)$ không có cực trị.
Đề: Tính đạo hàm các hàm số:a) $y=\frac{1}{\sqrt{x^2+1} }$b) $y=(\sqrt{x} +2)^3$
Đề bài: Tính đạo hàm các hàm số:a) $y=\frac{1}{\sqrt{x^2+1} }$b) $y=(\sqrt{x} +2)^3$ Lời giải a) $y=\frac{1}{\sqrt{x^2+1} }$ dạng $y=\frac{1}{v} $$y'=\frac{-v'}{v^2} $ với $v=\sqrt{x^2+1}$ (lại có dạng $v=\sqrt{u}$)$v'=\frac{u}{2\sqrt{u} }=\frac{(x^2+1)'}{2\sqrt{x^2+1} }=\frac{x}{\sqrt{x^2+1} }\Rightarrow y'=-\frac{\frac{x}{\sqrt{x^2+1} } }{(\sqrt{x^2+1)} ^2 … [Đọc thêm...] vềĐề: Tính đạo hàm các hàm số:a) $y=\frac{1}{\sqrt{x^2+1} }$b) $y=(\sqrt{x} +2)^3$
Đề: Tìm tập xác định của hàm số $y=\frac{5x+3} {|x^2-4|+|x^2-3x+2|}$
Đề bài: Tìm tập xác định của hàm số $y=\frac{5x+3} {|x^2-4|+|x^2-3x+2|}$ Lời giải Hàm số không xác định khi và chỉ khi $|x^2-4|+|x^2-3x+2|=0 \Leftrightarrow \left\{ \begin{array}{l} x^2-4=0\\ x^2-3x+2=0 \end{array} \right. $ $\Leftrightarrow \left\{ \begin{array}{l} … [Đọc thêm...] vềĐề: Tìm tập xác định của hàm số $y=\frac{5x+3} {|x^2-4|+|x^2-3x+2|}$