Đề: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$

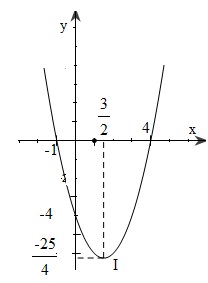
Đề bài: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$

Lời giải

Giải
* Tập xác định $R$
* Sự biến thiên:
   Ta có: $a=1>0, -\frac{b}{2a}=\frac{3}{2}, -\frac{\Delta}{4a}=-\frac{25}{4}$. Vậy đồ thị hàm số $y=x^2-3x-4$ là parabol có đỉnh $I(\frac{3}{2};-\frac{25}{4})$, nhận đường thẳng $x=\frac{3}{2}$ làm tâm đối xứng và bề lõm hướng lên trên.
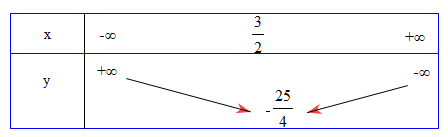
   Suy ra: Hàm số nghịch biến trên khoảng $(-\infty;\frac{3}{2})$ đồng biến trên khoảng $(\frac{3}{2};+\infty)$
Bảng biến thiên

Giá trị nhỏ nhất bằng $-\frac{25}{4}$, đạt được khi $x=\frac{3}{2}$
* Đồ thị
   Một số điểm khác thuộc đồ thị

Nối các điểm đó lại ta được parabol như hình dưới đây