
Đề bài: Cho hàm số:$y = {x^3} – 3{x^2} + 2$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số ($C$) của hàm số.$2$. Viết phương trình tiếp tuyến của ($C$) đi qua điểm $A(-1;-2)$$3$. Tìm tất cả các giá trị của tham số $a$ để phương trình ${x^3} – 3{x^2} – a = 0$ có $3$ nghiệm phân biệt, trong đó có đúng hai nghiệm lớn hơn $1$.
Lời giải
$1.$ $y=x^3-3x^2+2$
* TXĐ: $R$
* Sự biến thiên:
$\mathop {\lim y}\limits_{x \to + \infty }= \mathop {\lim x^3 \left ( 1-\frac{3}{x}+\frac{2}{x^3} \right ) }\limits_{x \to + \infty }=+ \infty $
$\mathop {\lim y}\limits_{x \to -\infty }=- \infty $
Có: $y’=3x^2-6x$
$y’=0 \Leftrightarrow \left[ \begin{gathered} x=0 \\ x=2 \end{gathered} \right. $
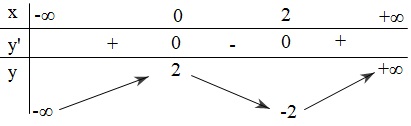
BBT: 
Hàm số đồng biến trên $(- \infty ; 0)$ và $(2;+\infty )$
Hàm số nghịch biến trên $(0;2)$
Hàm số đạt cực đại tại $x=0, y_{CĐ}=2$
Hàm số đạt cực tiểu tại $x=2, y_{CT}=-2$
* Đồ thị
$\cap Ox:$ $x^3-3x^2+2=0$
$\Leftrightarrow \left[ \begin{gathered} x=1 \\ x=1+\sqrt{3}\\x=1-\sqrt{3} \end{gathered} \right. $
Đồ thị hàm số cắt trục $Ox$ tại $(1;0), (1+\sqrt{3};0 )$ và $(1-\sqrt{3} ;0)$
Giao $Oy$ tại $(0;2)$
$y”=6x-6$
$y”=0 \Leftrightarrow x=1$
Vậy đồ thị hàm số nhận $(1;0)$ làm tâm đối xứng.
Đồ thị: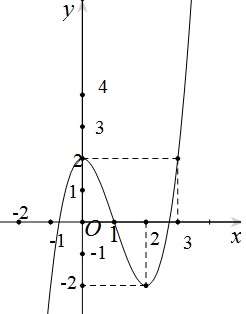
$2)$ Đường thẳng đi qua $A(-1;-2)$, hệ số góc k có phương trình: $y = k(x + 1) – 2.$
Đường thẳng này là tiếp tuyến khi và chỉ khi hệ pt sau có nghiệm:
$\left\{ \begin{array}{l}
{x^3} – 3{x^2} + 2 = k(x + 1) – 2\,\,\,(1)\\
3{x^2} – 6x = k\,\,\,(2)
\end{array} \right.$
Từ $(2)$ thế vào $(1)$ ta được:
$x^3-3x^2+2=(3x^2-6x)(x+1)-2$
$\Leftrightarrow 2x^3-6x-4=0$
$\Leftrightarrow (x+1)(2x^2-2x-4)=0$
$\Leftrightarrow \left[ \begin{gathered} x=-1 \\ x=2 \end{gathered} \right. $
$\Rightarrow \left[ \begin{gathered} k=9 \\ k=0 \end{gathered} \right. $
Vậy qua $A(-1 ;-2)$ kẻ được hai tiếp tuyến là $y = 9(x + 1) – 2 = 9x + 7$ và $y = 0(x+1) -2 =-2$
$3)$ Ta có: $x^3-3x^2-a=0 \Leftrightarrow x^3-3x^2+2=a+2(*)$
$(*)$ chính là phương trình hoành độ giao điểm của đồ thị hai hàm số:
$y=x^3-3x^2+2\,\,\,\,\,(C)$ và đường thẳng $y=a+2$ là đường song song với trục tung và cắt trục tung tại điểm có tung độ bằng $a+2$.
Số nghiệm của phương trình chính là số giao điểm của đồ thị hai hàm số, hoành độ giao điểm chính là nghiệm của phương trình.
Vậy từ đồ thị ta được phương trình muốn có 3 nghiệm phân biệt trong đó có đúng 2 nghiệm lớn hơn 1 $\Leftrightarrow -2
