
Đề bài: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị.
Lời giải
$1$. Bạn đọc tự giải.
$2$. Với \(m = 1\), có \(y = f\left( x \right) = – {x^4} + 2{x^2},\,f’\left( x \right) = – 4{x^3} + 4x\)
\(f’\left( {\sqrt 2 } \right) = – 4\sqrt 2 \). Tiếp tuyến tại điểm $A$ \(\left( {\sqrt 2 ,\,0} \right) \in (C)\) có phương trình
\(y = – 4\sqrt 2 .\left( {x – \sqrt 2 } \right) + 0 \Leftrightarrow y = – 4\sqrt 2 \left( {x – \sqrt 2 } \right)\)
$3$. \(y’ = – 4{x^3} + 4mx = – 4x\left( {{x^2} – m} \right)\)
Nếu \(m \le 0\) thì \({x^2} – m \ge 0,\,\,\forall x \Rightarrow y’\)
luôn cùng dấu với \( – 4x \Rightarrow y’\) đổi dấu đúng một lần.
Suy ra hàm số có một cực trị duy nhất.
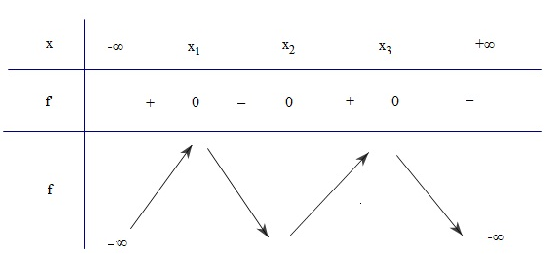
Nếu \(m > 0\) thì $y’ $ có $3$ nghiệm phân biệt \({x_1} = – \sqrt m ,\,\,{x_2} = 0,\,\,{x_3} = \sqrt m \)
Ta có bảng biến thiên như hình vẽ
Suy ra hàm số có $3$ cực trị.
Vậy \(\left( {{C_m}} \right)\) có $3$ cực trị \( \Leftrightarrow m > 0\).
