Đề: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} – 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$    $b)$ Qua điểm $A(1, 0)$  viết phương trình tiếp tuyến với đồ thị

Đề bài: Cho hàm số \(y = \frac{{{x^2} + {m^2}x + 2{m^2} – 5m + 3}}{x}\)$1$.Với giá trị dương nào của $m$ thì hàm số có cực tiểu nằm trong khoảng \(0 < x < 2m\).$2. a)$ Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m=2$    $b)$ Qua điểm $A(1, 0)$  viết phương trình tiếp tuyến với đồ thị

Lời giải

$1$. Ta có:
\(\begin{array}{l}
y = \frac{{{x^2} + {m^2}x + 2{m^2} – 5m + 3}}{x} = x + {m^2} + \frac{{2{m^2} – 5m + 3}}{x}\\
 \Rightarrow y’ = 1 – \frac{{2{m^2} – 5m + 3}}{{{x^2}}}
\end{array}\)
     – Nếu \(2{m^2} – 5m + 3 \le 0 \Rightarrow y’ > 0,\forall x \ne 0\)
Nên hàm số không có cực trị.
     – Nếu \(2{m^2} – 5m + 3 > 0\)
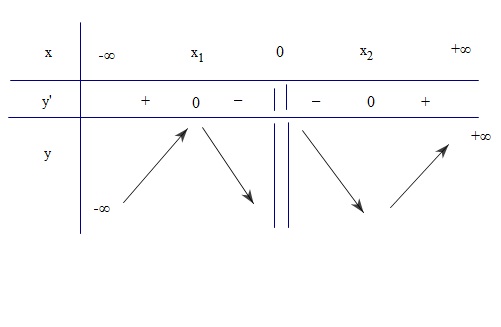
\( \Rightarrow y’\) có $2$ nghiệm phân biệt:  \({x_1} = -\sqrt {2{m^2} – 5m + 3} ;{x_2} = \sqrt {2{m^2} – 5m + 3} \)

Ta có bảng biến thiên như hình vẽ:

Hàm số có cực tiểu nằm trong khoảng: \(\begin{array}{l}
0 m > 0\\
0 \end{array} \right.\\
 \Leftrightarrow \left\{ \begin{array}{l}
m > 0\\
2{m^2} – 5m + 3 > 0\\
2{m^2} + 5m – 3 > 0
\end{array} \right.\\
 \Leftrightarrow \frac{1}{2} \frac{3}{2}
\end{array}\)

$2. a)$ Khi $m=2$ hàm số trở thành: \(y = x + 4 + \frac{1}{x}\). Bạn đọc tự khảo sát và vẽ đồ thị.

$b)$  Đường thẳng qua $A(1, 0)$ với hệ số góc $k$ có phương trình \(y = k\left( {x – 1} \right)\).
Đường thẳng này là tiếp tuyến \( \Leftrightarrow \) hệ phương trình ẩn $x$ sau có nghiệm: \(\left( H \right)\left\{ \begin{array}{l}
x + \frac{1}{x} + 4 = k\left( {x – 1} \right)\,\,\,\,\left( 1 \right)\\
1 – \frac{1}{{{x^2}}} = k\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)
\end{array} \right.\,\,\,\)
Lấy $(1)$ chia cho $x$ rồi trừ cho $(2)$, ta có:
\(\frac{2}{x} =  – 4 – k \Rightarrow \frac{1}{x} = \frac{{ – \left( {k + 4} \right)}}{2}\)
\(\left( H \right) \Leftrightarrow \left\{ \begin{array}{l}
1 – \frac{1}{{{x^2}}} = k\,\,\,\left( 2 \right)\\
\frac{1}{x} = \frac{{ – \left( {k + 4} \right)}}{2}\,\left( 3 \right)
\end{array} \right.\)
Hệ $(H)$ sẽ có nghiệm khi và chỉ khi $(3)$ có nghiệm thỏa mãn $(2)$ \( \Leftrightarrow \left\{ \begin{array}{l}
k + 4 \ne 0\\
1 – \frac{{{{\left( {k + 4} \right)}^2}}}{4} = k
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
k \ne  – 4\\
{k^2} + 12k + 12 = 0
\end{array} \right. \Leftrightarrow k =  – 6 \pm 2\sqrt 6 \)

Vậy có $2$ tiếp tuyến qua $A(1, 0)$. Phương trình $2$ tiếp tuyến đó là: \(y = \left( { – 6 + 2\sqrt 6 } \right)\left( {x – 1} \right);y = \left( {6 – 2\sqrt 6 } \right)\left( {x – 1} \right)\)