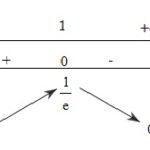
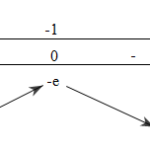
Đề bài: Cho hàm số: $y = \frac{{{x^2} + mx + 1}}{{x - 1}}$1) Tìm $m$ để hàm số đồng biến trên khoảng $\left( { - \infty ;1} \right)$ và trên $\left( {1; + \infty } \right)$.2) Tìm $m$ để tiệm cận xiên của đồ thị hàm số tạo với các trục tọa độ một tam giác có diện tích bằng 8 (diện tích đơn vị).3) Tìm $m$ để đường thẳng $y = m$ cắt đồ thị hàm số tại 2 điểm $A, B$ , … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{{x^2} + mx + 1}}{{x – 1}}$1) Tìm $m$ để hàm số đồng biến trên khoảng $\left( { – \infty ;1} \right)$ và trên $\left( {1; + \infty } \right)$.2) Tìm $m$ để tiệm cận xiên của đồ thị hàm số tạo với các trục tọa độ một tam giác có diện tích bằng 8 (diện tích đơn vị).3) Tìm $m$ để đường thẳng $y = m$ cắt đồ thị hàm số tại 2 điểm $A, B$ , $OA \bot OB$.4) Khảo sát sự biến thiên và vẽ đồ thị của hàm số ứng với $m = 1$
Kết quả tìm kiếm cho: ty so
Đề: Cho hàm số \(y=f(x)=\frac{x^{2}}{x^{2}+1}\) với \(x\geq 0\)Chứng minh rằng hàm số \(f(x)\) đơn điệu tăng trên khoảng \([0,+\infty]\)
Đề bài: Cho hàm số \(y=f(x)=\frac{x^{2}}{x^{2}+1}\) với \(x\geq 0\)Chứng minh rằng hàm số \(f(x)\) đơn điệu tăng trên khoảng \([0,+\infty]\) Lời giải Hàm số \(y=f(x)\) đơn điệu tăng trên \([0,+\infty)\)Ta có: \(y=f(x)=\frac{x^{2}+1-1}{x^{2}+1}=1-\frac{1}{x^{2}+1}\)Hàm số \(x^{2}+1\) đơn điệu tăng trên \([0,+\infty)\), tương tự hàm số \(-\frac{1}{x^{2}+1}\) cũng đơn điệu … [Đọc thêm...] vềĐề: Cho hàm số \(y=f(x)=\frac{x^{2}}{x^{2}+1}\) với \(x\geq 0\)Chứng minh rằng hàm số \(f(x)\) đơn điệu tăng trên khoảng \([0,+\infty]\)
Cho hàm số $f(x)$ có đạo hàm liên tục trên $[0; 1],$ thỏa $2f(x)+3f(1-x)=\sqrt{1-x^2}$. Giá trị của tích phân $\displaystyle\int\limits_0^1 f'(x)\mathrm{\,d}x$ bằng
Đề bài: Cho hàm số $f(x)$ có đạo hàm liên tục trên $[0; 1],$ thỏa $2f(x)+3f(1-x)=\sqrt{1-x^2}$. Giá trị của tích phân $\displaystyle\int\limits_0^1 f'(x)\mathrm{\,d}x$ bằng Các phương án chọn từ trên xuống là A B C D A. $0$ B. $\dfrac{1}{2}$ C. $1$ D. $\dfrac{3}{2}$ Lời Giải: Ta có $\displaystyle\int\limits_0^1 f'(x)\mathrm{\,d}x=f(x)\bigg|_0^1 =f(1)-f(0)$. Từ … [Đọc thêm...] vềCho hàm số $f(x)$ có đạo hàm liên tục trên $[0; 1],$ thỏa $2f(x)+3f(1-x)=\sqrt{1-x^2}$. Giá trị của tích phân $\displaystyle\int\limits_0^1 f'(x)\mathrm{\,d}x$ bằng
Đề: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm sốa) $f(x)=x^2 \ln x$ trên đoạn $[1;e].$b) $f(x)=x e^{-x}$ trên nửa khoảng $[0;\infty ).$
Đề bài: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm sốa) $f(x)=x^2 \ln x$ trên đoạn $[1;e].$b) $f(x)=x e^{-x}$ trên nửa khoảng $[0;\infty ).$ Lời giải a) Hàm số $f(x)=x^2 \ln x$ liên tục trên đoạn $[1;e]$ và có đạo hàm$f'(x)=2x \ln x+x^2 .\frac{1}{x}=x(2 \ln x+1), x\in [1;e]$$f'(x)=0\Leftrightarrow x=0\notin (1;e)$ hoặc $x=\frac{1}{\sqrt{e } }\notin [1;e]$và $f'(x) … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm sốa) $f(x)=x^2 \ln x$ trên đoạn $[1;e].$b) $f(x)=x e^{-x}$ trên nửa khoảng $[0;\infty ).$
Đề: Khảo sát sự biến thiên của hàm số $y=x^2+2x-2$ trên mỗi khoảng $(-\infty ;-1)$ và $(-1;+\infty .)$
Đề bài: Khảo sát sự biến thiên của hàm số $y=x^2+2x-2$ trên mỗi khoảng $(-\infty ;-1)$ và $(-1;+\infty .)$ Lời giải Xét tỷ số : $\frac{f(x_{2})-f(x_{1} ) }{x_{2} -x_{1} } =\frac{(x_{2}^2+2 x_{2}-2)-(x_{1}^2+2 x_{1}-2)}{x_{2}- x_{1} } = x_{1}+x_{2}+2.$ Trên khoảng $(-\infty ;-1)$ ta có $x_{1}nên suy ra hàm số nghịch biến.Tương tự, trên khoảng $(-1;+\infty )$, ta có … [Đọc thêm...] vềĐề: Khảo sát sự biến thiên của hàm số $y=x^2+2x-2$ trên mỗi khoảng $(-\infty ;-1)$ và $(-1;+\infty .)$
Đề: Cho hàm số: $y = \frac{2x^2 + kx + 2 – k}{x + k – 1}\,\,\,\,\,(1)$$1$. Khảo sát và vẽ đồ thị hàm số với $k = 0 (1).$$2$. Chứng minh rằng với mọi $k \ne 2$, đồ thị hàm số ($1$) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.$3$. Xác định $k$ để hàm số ($1$) đồng biến trên khoảng $(1; + \infty )$
Đề bài: Cho hàm số: $y = \frac{2x^2 + kx + 2 - k}{x + k - 1}\,\,\,\,\,(1)$$1$. Khảo sát và vẽ đồ thị hàm số với $k = 0 (1).$$2$. Chứng minh rằng với mọi $k \ne 2$, đồ thị hàm số ($1$) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.$3$. Xác định $k$ để hàm số ($1$) đồng biến trên khoảng $(1; + \infty )$ Lời giải $1.$ Xin dành cho bạn đọc. $2.$ Đồ thị qua … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{2x^2 + kx + 2 – k}{x + k – 1}\,\,\,\,\,(1)$$1$. Khảo sát và vẽ đồ thị hàm số với $k = 0 (1).$$2$. Chứng minh rằng với mọi $k \ne 2$, đồ thị hàm số ($1$) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.$3$. Xác định $k$ để hàm số ($1$) đồng biến trên khoảng $(1; + \infty )$
Đề: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$
Đề bài: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$ Lời giải a) $y=f(x)=\frac{1}{x e^x}, x\in (-\infty ;0)$Ta có $f'(x)=-\frac{(x e^x)'}{(x e^x)^2}=-\frac{(1+x)e^x}{(x e^x)^2}=-\frac{1+x}{x^2 e^x} $$f'(x)=0 \Leftrightarrow x=-1\in (-\infty ;0).$Trên … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất, giá trị nhỏ nhất (nếu có) của các hàm số sau:a) $y=\frac{1}{x e^x}$ trên khoảng $(- \infty ;0);$b) $y=\frac{x}{\ln x} $ trên khoảng $(1;+\infty )$
Đề: Cho hàm số: $y = \frac{{2{x^2} + ( {1 – m} )x + 1 + m}}{{x – m}}$ (1)1) Với $m = 1$, hãy khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng với mọi $m \ne – 1$, đồ thị hàm số (1) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.3) Xác định $m$ để hàm số (1) là đồng biến trên khoảng $\left( {1; + \infty } \right)$
Đề bài: Cho hàm số: $y = \frac{{2{x^2} + ( {1 - m} )x + 1 + m}}{{x - m}}$ (1)1) Với $m = 1$, hãy khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng với mọi $m \ne - 1$, đồ thị hàm số (1) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.3) Xác định $m$ để hàm số (1) là đồng biến trên khoảng $\left( {1; + \infty } \right)$ Lời … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{2{x^2} + ( {1 – m} )x + 1 + m}}{{x – m}}$ (1)1) Với $m = 1$, hãy khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng với mọi $m \ne – 1$, đồ thị hàm số (1) luôn tiếp xúc với một đường thẳng cố định tại một điểm cố định.3) Xác định $m$ để hàm số (1) là đồng biến trên khoảng $\left( {1; + \infty } \right)$
Đề: Cho hàm số $f(x)$ xác định bởi $f(x)=\begin{cases}x^2-x-2, với x \geq 3 \\ \frac{x-3}{\sqrt{x+1}-2 }, với -1< x< 3 \end{cases} $Chứng minh rằng hàm số $f(x)$ liên tục trên khoảng $(-1;+\infty)$.
Đề bài: Cho hàm số $f(x)$ xác định bởi $f(x)=\begin{cases}x^2-x-2, với x \geq 3 \\ \frac{x-3}{\sqrt{x+1}-2 }, với -1< x< 3 \end{cases} $Chứng minh rằng hàm số $f(x)$ liên tục trên khoảng $(-1;+\infty)$. Lời giải * Nếu $x>3: f(x)=x^2-x-2$ là hàm đa thức nên $f(x)$ liên tục trên $(3;+\infty ) (1)$* Nếu $-1 $\sqrt[]{x+1}-2 \neq 0 … [Đọc thêm...] vềĐề: Cho hàm số $f(x)$ xác định bởi $f(x)=\begin{cases}x^2-x-2, với x \geq 3 \\ \frac{x-3}{\sqrt{x+1}-2 }, với -1< x< 3 \end{cases} $Chứng minh rằng hàm số $f(x)$ liên tục trên khoảng $(-1;+\infty)$.
Đề: Cho hàm số $y = x^3 + (1 – 2m)x^2 + (2 – m)x + m + 2 (C).$ Tìm $m$ để hàm đồng biến trên $( 0; + \infty )$
Đề bài: Cho hàm số $y = x^3 + (1 - 2m)x^2 + (2 - m)x + m + 2 (C).$ Tìm $m$ để hàm đồng biến trên $( 0; + \infty )$ Lời giải Hàm đồng biến trên $\left( {0; + \infty } \right)$ $ \Leftrightarrow y' = 3{x^2} + 2(1 - 2m)x + (2 - m) \ge 0$ với $\forall x \in \left( {0; + \infty } \right)$Xét $ f\left( x \right) = \frac{{3{x^2} + 2x + 2}}{{4x + 1}} \ge m$ với $\forall x \in … [Đọc thêm...] vềĐề: Cho hàm số $y = x^3 + (1 – 2m)x^2 + (2 – m)x + m + 2 (C).$ Tìm $m$ để hàm đồng biến trên $( 0; + \infty )$