Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: hình bình hành có 1 góc vuông

Bài 1: Hình vuông – Tam giác đều – Lục giác đều – Toán lớp 6 (Tập 1) – Chân trời sáng tạo

Ngày Thuộc chủ đề:Giải bài tập Toán 6 - Chân trời sáng tạo Tag với:

Giải bài tập SGK Toán 6 - tập 1 - Sách Chân trời sáng tạo - Bài 1: Hình vuông – Tam giác đều – Lục giác đều ============ Bài 1: Hình vuông – Tam giác đều – Lục giác đều Thuộc CHƯƠNG 3. HÌNH HỌC TRỰC QUAN. CÁC HÌNH PHẲNG TRONG THỰC TIỄN ============= A. GIẢI CÂU HỎI LUYỆN TẬP VÀ VẬN DỤNG Hoạt động 1: Trang 75 Toán 6 tập 1 sgk chân trời sáng tạo Hướng dẫn:a) … [Đọc thêm...] vềBài 1: Hình vuông – Tam giác đều – Lục giác đều – Toán lớp 6 (Tập 1) – Chân trời sáng tạo

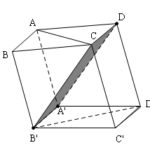
Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có điểm \(A\) trùng với gốc của hệ trục tọa độ, \(B(a;0;0)\), \(D(0;a;0)\), \(A'(0;0;b)\) \((a > 0,b > 0)\). Gọi \(M\) là trung điểm của cạnh \(CC’\). Giá trị của tỉ số \(\frac{a}{b}\) để hai mặt phẳng \((A’BD)\) và \(\left( {MBD} \right)\) vuông góc với nhau là

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình mặt phẳng Tag với:,

DẠNG TOÁN 50: PHƯƠNG TRÌNH MẶT PHẲNG (Tìm hệ số của phương trình mặt phẳng thỏa mãn các điều kiện cho trước lồng ghép với khối tròn xoay) =============== Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có điểm \(A\) trùng với gốc của hệ trục tọa độ, \(B(a;0;0)\), \(D(0;a;0)\), \(A'(0;0;b)\) \((a > 0,b > 0)\). Gọi \(M\) là trung điểm của cạnh \(CC'\). Giá … [Đọc thêm...] vềTrong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có điểm \(A\) trùng với gốc của hệ trục tọa độ, \(B(a;0;0)\), \(D(0;a;0)\), \(A'(0;0;b)\) \((a > 0,b > 0)\). Gọi \(M\) là trung điểm của cạnh \(CC’\). Giá trị của tỉ số \(\frac{a}{b}\) để hai mặt phẳng \((A’BD)\) và \(\left( {MBD} \right)\) vuông góc với nhau là

ĐỀ THI THỬ TN THPT môn Toán 2021 – sở GD&ĐT Ninh Bình – có lời giải

Ngày Thuộc chủ đề:Đề thi toán Tag với:

ĐỀ THI THỬ TN THPT môn Toán 2021 – sở GD&ĐT Ninh Bình - có lời giải ==== file pdf lời giải chi tiết + Cho tứ giác lồi có 4 đỉnh nằm trên đồ thị hàm số y = ln x, với hoành độ các đỉnh là các số nguyên dương liên tiếp. Biết diện tích của tứ giác đó là ln 21/20, khi đó hoành độ của đỉnh nằm thứ ba từ trái sang là? + Khi xây nhà, cô Ngọc cần xây một bể đựng nước mưa có thể … [Đọc thêm...] vềĐỀ THI THỬ TN THPT môn Toán 2021 – sở GD&ĐT Ninh Bình – có lời giải

Bài 2: Hai đường thẳng vuông góc – Hình học 11

Ngày Thuộc chủ đề:Toán lớp 11 Tag với:

Học Toán 11 Chương 3 Bài 2: Hai đường thẳng vuông góc 1. Tóm tắt lý thuyết 1.1. Tích vô hướng của hai vectơ trong không gian a) Góc giữa hai vectơ trong không gian – Định nghĩa:  Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) là hai vectơ khác vectơ – không. Lấy một điểm A bất kì, gọi B và C là hai điểm sao … [Đọc thêm...] vềBài 2: Hai đường thẳng vuông góc – Hình học 11

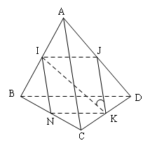
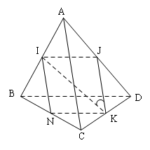
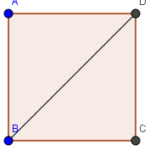
Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$ Lời giải cần giải chi tiết$a.$ Tức giác $IJKN$ là hình bình hành.$JK//AC$ nên góc giữa … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$

Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$ Lời giải cần giải chi tiết$a.$ Tức giác $IJKN$ là hình bình hành.$JK//AC$ nên góc giữa … [Đọc thêm...] vềĐề bài: Cho tứ diện $ABCD$;Gọi $I,J,K,N$ theo thứ tự là trung điểm của $AB,AD,CD,BC$$a.$ Chứng minh rằng góc giữa hai đường thẳng $IK,AC$ bằng góc giữa hai đường thẳng $IK,BD$ khi và chỉ khi $AC=BD$$b.$ Chứng minh rằng tam giác $INJ$ vuông tại $I$ khi và chỉ khi $AC\bot BD$

Đề bài: Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh cùng bằng nhau. Chứng minh rằng $AC\bot B'D'$. Nếu thêm giả thiết$\widehat{ABC}=\widehat{B'BA}=\widehat{B'BC}=60^0$Hãy chứng minh $A'B'CD$ là hình vuông.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh cùng bằng nhau. Chứng minh rằng $AC\bot B'D'$. Nếu thêm giả thiết$\widehat{ABC}=\widehat{B'BA}=\widehat{B'BC}=60^0$Hãy chứng minh $A'B'CD$ là hình vuông. Lời giải Ta có $AC\parallel A'C'$ và $A'B'C'D'$ là hình thoi nên $A'C' \perp B'D'$. Mà $A'C' \parallel AC$. … [Đọc thêm...] vềĐề bài: Cho hình hộp $ABCD.A'B'C'D'$ có tất cả các cạnh cùng bằng nhau. Chứng minh rằng $AC\bot B'D'$. Nếu thêm giả thiết$\widehat{ABC}=\widehat{B'BA}=\widehat{B'BC}=60^0$Hãy chứng minh $A'B'CD$ là hình vuông.

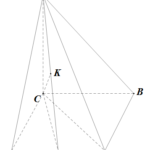
Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh $7a$, cạnh $SC$ vuông góc với mặt phẳng $(ABC)$ và $SC=7a$. Tìm khoảng cách giữa hai đường thẳng $SA$ và $BC$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh $7a$, cạnh $SC$ vuông góc với mặt phẳng $(ABC)$ và $SC=7a$. Tìm khoảng cách giữa hai đường thẳng $SA$ và $BC$. Lời giải Trong (ABC) dựng hình bình hành ADBCTrong (ADC) dựng CH$\bot$ADTrong (SCH) dựng CK$\bot$SHAD$\bot$CH; AD$\bot$SC$\Rightarrow $AD$\bot$ (SCH) $\Rightarrow$ AD $\bot$ CK mà … [Đọc thêm...] vềĐề bài: Cho hình chóp tam giác $S.ABC$ có đáy là tam giác đều cạnh $7a$, cạnh $SC$ vuông góc với mặt phẳng $(ABC)$ và $SC=7a$. Tìm khoảng cách giữa hai đường thẳng $SA$ và $BC$.

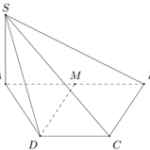
Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng.

Ngày Thuộc chủ đề:Trắc nghiệm Khoảng cách và góc trong không gian Tag với:

Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng. A. \(\frac{{3a}}{4}\). B. \(\frac{{3a}}{2}\). C. \(\frac{{3\sqrt {13} a}}{{13}}\). D. \(\frac{{6\sqrt … [Đọc thêm...] vềCâu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng.

XÁC ĐỊNH BIỂU THỨC TÍCH VÔ HƯỚNG – GÓC GIỮA HAI VECTƠ

Ngày Thuộc chủ đề:Toán lớp 10 Tag với:

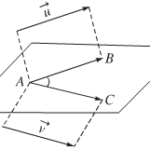
DẠNG TOÁN 1: XÁC ĐỊNH BIỂU THỨC TÍCH VÔ HƯỚNG – GÓC GIỮA HAI VECTƠ. 1. PHƯƠNG PHÁP GIẢI Dựa vào định nghĩa $\vec a.\vec b = |\vec a|.|\vec b|\cos (\vec a;\vec b).$ Sử dụng tính chất và các hằng đẳng thức của tích vô hướng của hai vectơ. 2. CÁC VÍ DỤ Bài 1: Tính tích vô hướng của \(\vec{a}(2;3)\) và \(\vec{b}(1;1)\) biết chúng tạo với nhau một góc \(30^o\) Hướng … [Đọc thêm...] vềXÁC ĐỊNH BIỂU THỨC TÍCH VÔ HƯỚNG – GÓC GIỮA HAI VECTƠ