Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng.

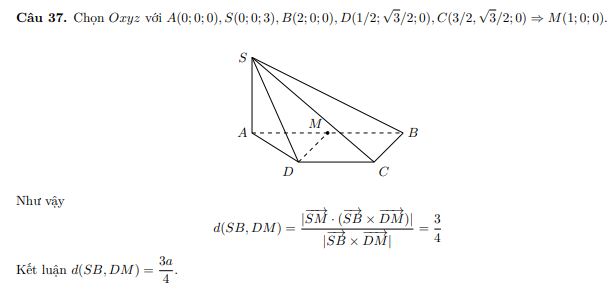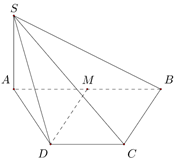
Câu 37: (MH Toan 2020) Cho hình chóp \(S.ABCD\) có đáy là hình thang, \(AB = 2a\), \(AD = DC = CB = a\), \(SA\) vuông góc với mặt phẳng đáy và \(SA = 3a\) (minh họa như hình bên). Gọi \(M\) là trung điểm của \(AB\). Khoảng cách giữa hai đường thẳng \(SB\) và \(DM\) bằng.
A. \(\frac{{3a}}{4}\).
B. \(\frac{{3a}}{2}\).
C. \(\frac{{3\sqrt {13} a}}{{13}}\).
D. \(\frac{{6\sqrt {13} a}}{{13}}\).

Lời giải

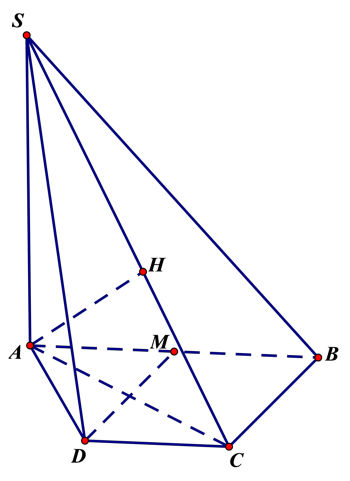
Đáp án: A
Ta có \(M\) là trung điểm của \(AB\) nên \(AM = MB = a\).
\( \Rightarrow MB = DC = a\) và \(MN\;//\;DC\)
\( \Rightarrow \) \(MDCB\) là hình bình hành\( \Rightarrow MD\;//\;BC\)\( \Rightarrow MD\;//\;(SBC)\)
\( \Rightarrow d(SB,DM) = d(DM,(SBC)) = d(M,(SBC))\)
Ta có \(AM = DC = a\) và \(AM\;//\;DC\) nên \(AMCD\) là hình bình hành
\( \Rightarrow MC = AD = a\)
Xét tam giác \(ACB\), ta có \(AM = MB = MC = a\), \(M\) là trung điểm \(AB\)
\( \Rightarrow \) \(\Delta ACB\) vuông tại \(C\) \( \Rightarrow AC \bot CB\)
Vì \(SA\) vuông góc với đáy \( \Rightarrow SA \bot CB\)
\( \Rightarrow CB \bot (SAC)\); Mà \(CB \subset (SCB)\)
\( \Rightarrow (SBC) \bot (SAC)\)
Trong mặt phẳng \((SAC)\) kẻ, \(AH \bot SC\), \(H \in SC\)
\( \Rightarrow AH \bot (SCB)\)\( \Rightarrow d(A,(SCB)) = AH\)
Xét tam giác \(ABC\) vuông tại \(C\), ta có \(AC = \sqrt {A{B^2} – B{C^2}} = a\sqrt 3 \)
Xét tam giác \(SAC\) vuông tại \(A\) có \(AH\) là đường cao
\( \Rightarrow \) \(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{C^2}}} = \frac{4}{{9{a^2}}}\)\( \Rightarrow AH = \frac{{3a}}{2}\)
Ta có \(AM \cap (SBC) = B\) và \(BM = \frac{1}{2}BA\)
\( \Rightarrow d(M,(SBC)) = \frac{1}{2}d(A,(SBC)) = \frac{1}{2}.\frac{{3a}}{2} = \frac{{3a}}{4}\).
————–
Cách 2: Phương pháp tọa độ hóa