Cho hình chóp tam giác đều \(S.ABC\) có tất các cạnh đều bằng \(a\).Gọi \(O\) là tâm của tam giác \(ABC\).Tính khoảng cách từ \(O\) đến \((SCB)\).

A. \(d\left( {O,\left( {SCB} \right)} \right) = \frac{{a\sqrt {54} }}{2}\).

B. \(d\left( {O,\left( {SCB} \right)} \right) = \frac{{a\sqrt {54} }}{4}\).

C. \(d\left( {O,\left( {SCB} \right)} \right) = \frac{{a\sqrt 3 }}{2}\).

D. \(d\left( {O,\left( {SCB} \right)} \right) = \frac{{a\sqrt {27} }}{2}\).

Lời giải:

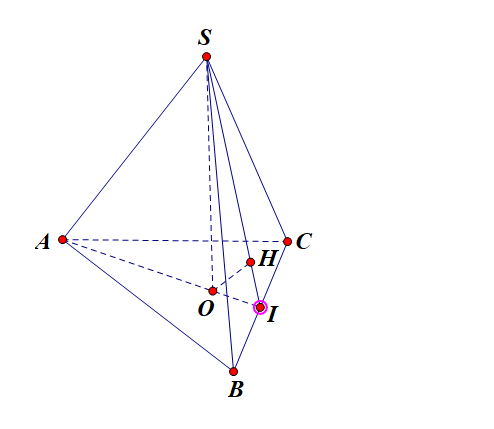
Do \(S.ABC\) là hình chóp đều nên \(SO \bot \left( {ABC} \right) \Rightarrow SO \bot CB\)

Gọi \(I\) là trung điểm \(CB\), ta có \(OI \bot CB,OI = \frac{1}{3}AI = \frac{{\sqrt 3 }}{6}a\).

Trong tam giác \(SOI\) kẻ \(OH \bot SI\). Ta có \(\left\{ \begin{array}{l}CB \bot OI\\CB \bot SO\end{array} \right. \Rightarrow CB \bot (SOI) \supset OH \Rightarrow CB \bot OH\).

Mặt khác ta có \(\left\{ \begin{array}{l}OH \bot SI\\OH \bot CB\end{array} \right. \Rightarrow OH \bot (SCB) \Rightarrow d\left( {O,(SCB)} \right) = OH\).

Ta có \(SO = \sqrt {S{C^2} – O{C^2}} = \sqrt {{a^2} – {{\left( {\frac{{a\sqrt 3 }}{3}} \right)}^2}} = \frac{{a\sqrt 6 }}{3}\)

\(\frac{1}{{O{H^2}}} = \frac{1}{{O{I^2}}} + \frac{1}{{S{O^2}}} = \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{6}} \right)}^2}}} + \frac{1}{{{{\left( {\frac{{\sqrt 6 a}}{3}} \right)}^2}}} = \frac{{27}}{{2{a^2}}} \Rightarrow OH = \frac{{a\sqrt {27} }}{{\sqrt 2 }}\).

Vậy \(d\left( {O,\left( {SCB} \right)} \right) = \frac{{a\sqrt {54} }}{2}\).