DẠNG TOÁN 1: XÁC ĐỊNH BIỂU THỨC TÍCH VÔ HƯỚNG – GÓC GIỮA HAI VECTƠ.
1. PHƯƠNG PHÁP GIẢI
Dựa vào định nghĩa $\vec a.\vec b = |\vec a|.|\vec b|\cos (\vec a;\vec b).$
Sử dụng tính chất và các hằng đẳng thức của tích vô hướng của hai vectơ.
2. CÁC VÍ DỤ
Bài 1:
Tính tích vô hướng của \(\vec{a}(2;3)\) và \(\vec{b}(1;1)\) biết chúng tạo với nhau một góc \(30^o\)
Hướng dẫn:
Áp dụng công thức tính tích vô hướng của hai vectơ, ta có: \(\vec{a}.\vec{b}=|\vec{a}|.|\vec{b}|.cos30\)
\(=\sqrt{2^2+3^2}.\sqrt{1^2+1^2}.\frac{\sqrt{3}}{2}=\frac{\sqrt{78}}{2}\)
Bài 2:
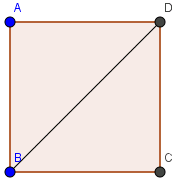
Cho hình vuông ABCD cạnh a đường chéo BD. Tính các tích vô hướng sau: \(\vec{AD}.\vec{AB}\), \(\vec{AD}.\vec{BD}\) và \(\vec{AB}.\vec{CD}\)
Hướng dẫn:

Vì \(AD\perp AB\) nên \(\vec{AD}.\vec{AB}=0\)
\(\vec{AD}.\vec{BD}=|\vec{AD}|.|\vec{BD}|cosADB=a.a\sqrt{2}.cos45=a^2\)
\(\vec{AB}.\vec{CD}=|\vec{AB}|.|\vec{CD}|.cos0^o=a^2\)
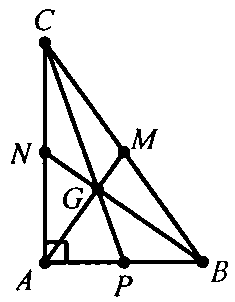
Ví dụ 3 : Cho tam giác $ABC$ vuông tại $A$ có $AB = a$, $BC = 2a$ và $G$ là trọng tâm.
a) Tính các tích vô hướng: $\overrightarrow {BA} .\overrightarrow {BC} $, $\overrightarrow {BC} .\overrightarrow {CA} .$
b) Tính giá trị của biểu thức: $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} .$
c) $\overrightarrow {GA} .\overrightarrow {GB} + \overrightarrow {GB} .\overrightarrow {GC} + \overrightarrow {GC} .\overrightarrow {GA} .$
a) Theo định nghĩa tích vô hướng ta có:
$\overrightarrow {BA} .\overrightarrow {BC} $ $ = |\overrightarrow {BA} |.|\overrightarrow {BC} |\cos (\overrightarrow {BA} ,\overrightarrow {BC} )$ $ = 2{a^2}\cos (\overrightarrow {BA} ,\overrightarrow {BC} ).$
Mặt khác $\cos (\overrightarrow {BA} ,\overrightarrow {BC} )$ $ = \cos \widehat {ABC}$ $ = \frac{a}{{2a}} = \frac{1}{2}.$
Nên $\overrightarrow {BA} .\overrightarrow {BC} = {a^2}.$
Ta có $\overrightarrow {BC} .\overrightarrow {CA} = – \overrightarrow {CB} .\overrightarrow {CA} $ $ = – |\overrightarrow {CB} |.|\overrightarrow {CA} |\cos \widehat {ACB}.$
Theo định lý Pitago ta có $CA = \sqrt {{{(2a)}^2} – {a^2}} = a\sqrt 3 .$
Suy ra $\overrightarrow {BC} .\overrightarrow {CA} $ $ = – a\sqrt 3 .2a.\frac{{a\sqrt 3 }}{{2a}} = – 3{a^2}.$
b) Cách 1: Vì tam giác $ABC$ vuông tại $A$ nên $\overrightarrow {CA} .\overrightarrow {AB} = 0$ và từ câu a ta có: $\overrightarrow {AB} .\overrightarrow {BC} = – {a^2}$, $\overrightarrow {BC} .\overrightarrow {CA} = – 3{a^2}.$
Suy ra $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} = – 4{a^2}.$
Cách 2: Từ $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \vec 0$ và hằng đẳng thức:
${(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} )^2}$ $ = A{B^2} + B{C^2} + C{A^2}$ $ + 2(\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} ).$
Ta có: $\overrightarrow {AB} .\overrightarrow {BC} + \overrightarrow {BC} .\overrightarrow {CA} + \overrightarrow {CA} .\overrightarrow {AB} $ $ = – \frac{1}{2}\left( {A{B^2} + B{C^2} + C{A^2}} \right)$ $ = – 4{a^2}.$
c) Tương tự cách 2 của câu b vì: $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0$ nên:
$\overrightarrow {GA} .\overrightarrow {GB} + \overrightarrow {GB} .\overrightarrow {GC} + \overrightarrow {GC} .\overrightarrow {GA} $ $ = – \frac{1}{2}\left( {G{A^2} + G{B^2} + G{C^2}} \right).$
Gọi $M$, $N$, $P$ lần lượt là trung điểm của $BC$, $CA$, $AB.$
Dễ thấy tam giác $ABM$ đều nên $G{A^2} = {\left( {\frac{2}{3}AM} \right)^2} = \frac{{4{a^2}}}{9}.$
Theo định lý Pitago ta có:
$G{B^2} = \frac{4}{9}B{N^2}$ $ = \frac{4}{9}\left( {A{B^2} + A{N^2}} \right)$ $ = \frac{4}{9}\left( {{a^2} + \frac{{3{a^2}}}{4}} \right)$ $ = \frac{{7{a^2}}}{9}.$
$G{C^2} = \frac{4}{9}C{P^2}$ $ = \frac{4}{9}\left( {A{C^2} + A{P^2}} \right)$ $ = \frac{4}{9}\left( {3{a^2} + \frac{{{a^2}}}{4}} \right)$ $ = \frac{{13{a^2}}}{9}.$
Suy ra: $\overrightarrow {GA} .\overrightarrow {GB} + \overrightarrow {GB} .\overrightarrow {GC} + \overrightarrow {GC} .\overrightarrow {GA} $ $ = – \frac{1}{2}\left( {\frac{{4{a^2}}}{9} + \frac{{7{a^2}}}{9} + \frac{{13{a^2}}}{9}} \right)$ $ = – \frac{{4{a^2}}}{3}.$
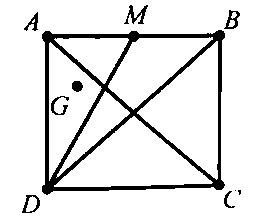
Ví dụ 4 : Cho hình vuông $ABCD$ cạnh $a.$ $M$ là trung điểm của $AB$, $G$ là trọng tâm tam giác $ADM.$ Tính giá trị các biểu thức sau:
a) $(\overrightarrow {AB} + \overrightarrow {AD} )(\overrightarrow {BD} + \overrightarrow {BC} ).$
b) $\overrightarrow {CG} .(\overrightarrow {CA} + \overrightarrow {DM} ).$
a) Theo quy tắc hình bình hành ta có $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} .$
Do đó $(\overrightarrow {AB} + \overrightarrow {AD} )(\overrightarrow {BD} + \overrightarrow {BC} )$ $ = \overrightarrow {AC} .\overrightarrow {BD} + \overrightarrow {AC} .\overrightarrow {BC} $ $ = \overrightarrow {CA} .\overrightarrow {CB} $ $ = |\overrightarrow {CA} |.|\overrightarrow {CB} |\cos \widehat {ACB}$ ($\overrightarrow {AC} .\overrightarrow {BD} = 0$ vì $\overrightarrow {AC} \bot \overrightarrow {BD} $).
Mặt khác $\widehat {ACB} = {45^0}$ và theo định lý Pitago ta có:
$AC = \sqrt {{a^2} + {a^2}} = a\sqrt 2 .$
Suy ra $(\overrightarrow {AB} + \overrightarrow {AD} )(\overrightarrow {BD} + \overrightarrow {BC} )$ $ = a.a\sqrt 2 \cos {45^0} = {a^2}.$
b) Vì $G$ là trọng tâm tam giác $ADM$ nên $\overrightarrow {CG} = \overrightarrow {CD} + \overrightarrow {CA} + \overrightarrow {CM} .$
Mặt khác theo quy tắc hình bình hành và hệ thức trung điểm ta có:
$\overrightarrow {CA} = – (\overrightarrow {AB} + \overrightarrow {AD} ).$
$\overrightarrow {CM} = \frac{1}{2}(\overrightarrow {CB} + \overrightarrow {CA} )$ $ = \frac{1}{2}[\overrightarrow {CB} – (\overrightarrow {AB} + \overrightarrow {AD} )]$ $ = – \frac{1}{2}(\overrightarrow {AB} + 2\overrightarrow {AD} ).$
Suy ra $\overrightarrow {CG} = – \overrightarrow {AB} – (\overrightarrow {AB} + \overrightarrow {AD} )$ $ – \frac{1}{2}(\overrightarrow {AB} + 2\overrightarrow {AD} )$ $ = – \left( {\frac{5}{2}\overrightarrow {AB} + 2\overrightarrow {AD} } \right).$
Ta lại có $\overrightarrow {CA} + \overrightarrow {DM} $ $ = – (\overrightarrow {AB} + \overrightarrow {AD} ) + \overrightarrow {AM} – \overrightarrow {AD} $ $ = – \left( {\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AD} } \right).$
Nên $\overrightarrow {CG} .(\overrightarrow {CA} + \overrightarrow {DM} )$ $ = \left( {\frac{5}{2}\overrightarrow {AB} + 2\overrightarrow {AD} } \right)\left( {\frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {AD} } \right)$ $ = \frac{5}{4}A{B^2} + 4A{D^2}$ $ = \frac{{21{a^2}}}{4}.$
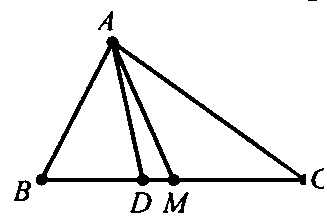
Ví dụ 5 : Cho tam giác $ABC$ có $BC = a$, $CA = b$, $AB = c.$ $M$ là trung điểm của $BC$, $D$ là chân đường phân giác trong góc $A.$
a) Tính $\overrightarrow {AB} .\overrightarrow {AC} $ rồi suy ra $\cos A.$
b) Tính ${\overrightarrow {AM} ^2}$ và ${\overrightarrow {AD} ^2}.$
a) Ta có $\overrightarrow {AB} .\overrightarrow {AC} $ $ = \frac{1}{2}\left[ {{{\overrightarrow {AB} }^2} + {{\overrightarrow {AC} }^2} – {{(\overrightarrow {AB} – \overrightarrow {AC} )}^2}} \right]$ $ = \frac{1}{2}\left[ {A{B^2} + A{C^2} – C{B^2}} \right]$ $ = \frac{1}{2}\left( {{c^2} + {b^2} – {a^2}} \right).$
Mặt khác $\overrightarrow {AB} .\overrightarrow {AC} $ $ = AB.AC\cos A$ $ = cb\cos A.$
Suy ra $\frac{1}{2}\left( {{c^2} + {b^2} – {a^2}} \right) = cb\cos A$ hay $\cos A = \frac{{{c^2} + {b^2} – {a^2}}}{{2bc}}.$
b) Vì $M$ là trung điểm của $BC$ nên $\overrightarrow {AM} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {AC} ).$
Suy ra ${\overrightarrow {AM} ^2} = \frac{1}{4}{(\overrightarrow {AB} + \overrightarrow {AC} )^2}$ $ = \frac{1}{4}\left( {{{\overrightarrow {AB} }^2} + 2\overrightarrow {AB} .\overrightarrow {AC} + {{\overrightarrow {AC} }^2}} \right).$
Theo câu a ta có: $\overrightarrow {AB} .\overrightarrow {AC} = \frac{1}{2}\left( {{c^2} + {b^2} – {a^2}} \right)$ nên ${\overrightarrow {AM} ^2}$ $ = \frac{1}{4}\left( {{c^2} + 2.\frac{1}{2}\left( {{c^2} + {b^2} – {a^2}} \right) + {b^2}} \right)$ $ = \frac{{2\left( {{b^2} + {c^2}} \right) – {a^2}}}{4}.$
Theo tính chất đường phân giác thì $\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{c}{b}.$
Suy ra $\overrightarrow {BD} = \frac{{BD}}{{DC}}\overrightarrow {DC} = \frac{b}{c}\overrightarrow {DC} $ $(*).$
Mặt khác $\overrightarrow {BD} = \overrightarrow {AD} – \overrightarrow {AB} $ và $\overrightarrow {DC} = \overrightarrow {AC} – \overrightarrow {AD} $ thay vào $(*)$ ta được:
$\overrightarrow {AD} – \overrightarrow {AB} $ $ = \frac{b}{c}(\overrightarrow {AC} – \overrightarrow {AD} )$ $ \Leftrightarrow (b + c)\overrightarrow {AD} = b\overrightarrow {AB} + c\overrightarrow {AC} .$
$ \Leftrightarrow {(b + c)^2}{\overrightarrow {AD} ^2}$ $ = {(b\overrightarrow {AB} )^2} + 2bc\overrightarrow {AB} .\overrightarrow {AC} + {(c\overrightarrow {AC} )^2}.$
$ \Leftrightarrow {(b + c)^2}{\overrightarrow {AD} ^2}$ $ = {b^2}{c^2} + 2bc.\frac{1}{2}\left( {{c^2} + {b^2} – {a^2}} \right) + {c^2}{b^2}.$
$ \Leftrightarrow {\overrightarrow {AD} ^2}$ $ = \frac{{bc}}{{{{(b + c)}^2}}}(b + c – a)(b + c + a).$
Hay ${\overrightarrow {AD} ^2} = \frac{{4bc}}{{{{(b + c)}^2}}}p(p – a).$
Nhận xét: Từ câu b suy ra độ dài đường phân giác kẻ từ đỉnh $A$ là:
${l_a} = \frac{{2\sqrt {bc} }}{{b + c}}\sqrt {p(p – a)} .$
