BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG

DẠNG TOÁN 4: BIỂU THỨC TỌA ĐỘ CỦA TÍCH VÔ HƯỚNG.
1. PHƯƠNG PHÁP GIẢI
Cho $\vec a = \left( {{x_1};{y_1}} \right)$, $\vec b = \left( {{x_2};{y_2}} \right).$ Khi đó:
+ Tích vô hướng hai vectơ là $\vec a.\vec b = {x_1}{x_2} + {y_1}{y_2}.$
+ Góc của hai vectơ được xác định bởi công thức:
$\cos (\vec a,\vec b) = \frac{{\vec a.\vec b}}{{|\vec a||\vec b|}}$ $ = \frac{{{x_1}{x_2} + {y_1}{y_2}}}{{\sqrt {x_1^2 + y_1^2} \sqrt {x_2^2 + y_2^2} }}.$
Chú ý: $\vec a \bot \vec b$ $ \Leftrightarrow \vec a.\vec b = 0$ $ \Leftrightarrow {x_1}{x_2} + {y_1}{y_2} = 0.$
Để xác định độ dài một vectơ đoạn thẳng ta sử dụng công thức:
+ Nếu $\vec a = (x;y)$ thì $|\vec a| = \sqrt {{x^2} + {y^2}} .$
+ Nếu $A\left( {{x_A};{y_A}} \right)$, $B\left( {{x_B};{y_B}} \right)$ thì $AB = \sqrt {{{\left( {{x_B} – {x_A}} \right)}^2} + {{\left( {{y_B} – {y_A}} \right)}^2}} .$

2. CÁC VÍ DỤ
Ví dụ 1 : Cho tam giác $ABC$ có $A(1;2)$, $B( – 2;6)$, $C(9;8).$
a) Chứng minh tam giác $ABC$ vuông tại $A.$
b) Tính góc $B$ của tam giác $ABC.$
c) Xác định hình chiếu của $A$ lên cạnh $BC.$

a) Ta có $\overrightarrow {AB} ( – 3;4)$, $\overrightarrow {AC} (8;6)$ $ \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = – 3.8 + 4.6 = 0.$
Do đó $\overrightarrow {AB} \bot \overrightarrow {AC} $ hay tam giác $ABC$ vuông tại $A.$
b) Ta có $\overrightarrow {BC} (11;2)$, $\overrightarrow {BA} (3; – 4).$
Suy ra $\cos B = \cos (\overrightarrow {BC} ,\overrightarrow {BA} )$ $ = \frac{{11.3 + 2.( – 4)}}{{\sqrt {{{11}^2} + {2^2}} \sqrt {{3^2} + {{( – 4)}^2}} }}$ $ = \frac{1}{{\sqrt 5 }}.$
c) Gọi $H(x;y)$ là hình chiếu của $A$ lên $BC.$
Ta có $\overrightarrow {AH} (x – 1;y – 2)$, $\overrightarrow {BH} (x + 2;y – 6)$, $\overrightarrow {BC} (11;2).$
$AH \bot BC$ $ \Leftrightarrow \overrightarrow {AH} .\overrightarrow {BC} = 0$ $ \Leftrightarrow 11(x – 1) + 2(y – 2) = 0.$
Hay $11x + 2y – 15 = 0$ $(1).$
Mặt khác $\overrightarrow {BH} $, $\overrightarrow {BC} $ cùng phương nên $\frac{{x + 2}}{{11}} = \frac{{y – 6}}{2}$ $ \Leftrightarrow 2x – 11y + 70 = 0$ $(2).$
Từ $(1)$ và $(2)$ suy ra $x = \frac{1}{5}$, $y = \frac{{32}}{5}.$
Vậy hình chiếu của $A$ lên $BC$ là $H\left( {\frac{1}{5};\frac{{32}}{5}} \right).$

Ví dụ 2 : Cho hình thoi $ABCD$ có tâm $I(1;1)$, đỉnh $A(3;2)$ và đỉnh $B$ nằm trên trục hoành. Tìm tọa độ các đỉnh còn lại của hình thoi.

Vì $B$ nằm trên trục hoành nên giả sử $B(0;y).$
Vì $I$ là tâm hình thoi $ABCD$ nên $I$ là trung điểm của $AC$ và $BD.$
Suy ra $C = \left( {2{x_I} – {x_A};2{y_I} – {y_A}} \right)$ $ = ( – 1;0)$, $D = \left( {2{x_I} – {x_B};2{y_I} – {y_B}} \right)$ $ = (2;2 – y).$
Do đó $AB = AD$ $ \Leftrightarrow A{B^2} = A{D^2}$ $ \Leftrightarrow 9 + {(y – 2)^2} = 1 + {y^2}$ $ \Leftrightarrow y = 3.$
Vậy $B(0;3)$, $C( – 1;0)$, $D(2; – 1).$

Ví dụ 3 : Cho ba điểm $A(3;4)$, $B(2;1)$ và $C( – 1; – 2).$ Tìm điểm $M$ trên đường thẳng $BC$ để góc $\widehat {AMB} = {45^0}.$

Giả sử $M(x;y)$ suy ra $\overrightarrow {MA} (3 – x;4 – y)$, $\overrightarrow {MB} (2 – x;1 – y)$, $\overrightarrow {BC} ( – 3; – 3).$
Vì $\widehat {AMB} = {45^0}$ suy ra $|\cos \widehat {AMB}| = |\cos (\overrightarrow {MA} ;\overrightarrow {BC} )|.$
$ \Leftrightarrow \cos {45^0} = \frac{{|\overrightarrow {MA} .\overrightarrow {BC} |}}{{|\overrightarrow {MA} |.|\overrightarrow {BC} |}}$ $ \Leftrightarrow \frac{{\sqrt 2 }}{2} = \frac{{| – 3(3 – x) – 3(4 – y)|}}{{\sqrt {{{(3 – x)}^2} + {{(4 – y)}^2}} \sqrt {9 + 9} }}.$
$ \Leftrightarrow \sqrt {{{(3 – x)}^2} + {{(4 – y)}^2}} $ $ = |x + y – 7|$ $(*).$
Mặt khác $M$ thuộc đường thẳng $BC$ nên hai vectơ $\overrightarrow {MB} $, $\overrightarrow {BC} $ cùng phương.
Suy ra $\frac{{2 – x}}{{ – 3}} = \frac{{1 – y}}{{ – 3}}$ $ \Leftrightarrow x = y + 1$ thế vào $(*)$ ta được:
$\sqrt {{{(2 – y)}^2} + {{(4 – y)}^2}} $ $ = |2y – 6|$ $ \Leftrightarrow {y^2} – 6y + 8 = 0$ $ \Leftrightarrow y = 2$ hoặc $y = 4.$
+ Với $y = 2 \Rightarrow x = 3$, ta có:
$\overrightarrow {MA} (0;2)$, $\overrightarrow {MB} ( – 1; – 1)$ $ \Rightarrow \cos \widehat {AMB}$ $ = \cos (\overrightarrow {MA} ;\overrightarrow {MB} )$ $ = – \frac{1}{{\sqrt 2 }}.$
Khi đó $\widehat {AMB} = {135^0}$ (không thỏa mãn).
+ Với $y = 4 \Rightarrow x = 5$, ta có:
$\overrightarrow {MA} ( – 2;0)$, $\overrightarrow {MB} ( – 3; – 3)$ $ \Rightarrow \cos \widehat {AMB}$ $ = \cos (\overrightarrow {MA} ;\overrightarrow {MB} )$ $ = \frac{1}{{\sqrt 2 }}.$
Khi đó $\widehat {AMB} = {45^0}.$
Vậy $M(5;4)$ là điểm cần tìm.

Ví dụ 4 : Cho điểm $A(2;1).$ Lấy điểm $B$ nằm trên trục hoành có hoành độ không âm và điểm $C$ trên trục tung có tung độ dương sao cho tam giác $ABC$ vuông tại $A.$ Tìm toạ độ $B$, $C$ để tam giác $ABC$ có diện tích lớn nhất.

Gọi $B(b;0)$, $C(0;c)$ với $b \ge 0$, $c > 0.$
Suy ra $\overrightarrow {AB} (b – 2; – 1)$, $\overrightarrow {AC} ( – 2;c – 1).$
Theo giả thiết ta có tam giác $ABC$ vuông tại $A$ nên:
$\overrightarrow {AB} .\overrightarrow {AC} = 0$ $ \Leftrightarrow (b – 2)( – 2) – 1.(c – 1) = 0$ $ \Leftrightarrow c = – 2b + 5.$
Ta có ${S_{\Delta ABC}} = \frac{1}{2}AB.AC$ $ = \frac{1}{2}\sqrt {{{(b – 2)}^2} + 1} .\sqrt {{2^2} + {{(c – 1)}^2}} $ $ = {(b – 2)^2} + 1$ $ = {b^2} – 4b + 5.$
Vì $c > 0$ nên $ – 2b + 5 > 0$ $ \Rightarrow 0 \le b < \frac{5}{2}.$
Xét hàm số $y = {x^2} – 4x + 5$ với $0 \le x < \frac{5}{2}.$
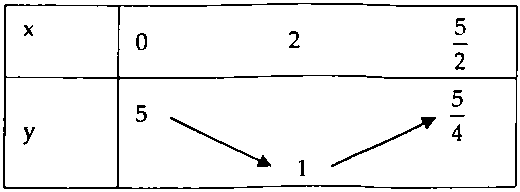
Bảng biến thiên:

Suy ra giá trị lớn nhất của hàm số $y = {x^2} – 4x + 5$ với $0 \le x < \frac{5}{2}$ là $y = 5$ khi $x =0.$
Do đó diện tích tam giác $ABC$ lớn nhất khi và chỉ khi $b = 0$, suy ra $c=5.$
Vậy $B(0;0)$, $C(0;5)$ là điểm cần tìm.