CHỨNG MINH CÁC ĐẲNG THỨC VỀ TÍCH VÔ HƯỚNG HOẶC ĐỘ DÀI CỦA ĐOẠN THẲNG

DẠNG TOÁN 2: CHỨNG MINH CÁC ĐẲNG THỨC VỀ TÍCH VÔ HƯỚNG HOẶC ĐỘ DÀI CỦA ĐOẠN THẲNG.
1. PHƯƠNG PHÁP GIẢI
Nếu trong đẳng thức chứa bình phương độ dài của đoạn thẳng thì ta chuyển về vectơ nhờ đẳng thức $A{B^2} = {\overrightarrow {AB} ^2}.$
Sử dụng các tính chất của tích vô hướng, các quy tắc phép toán vectơ.
Sử dụng hằng đẳng thức vectơ về tích vô hướng.

2. CÁC VÍ DỤ
Ví dụ 1: Cho $I$ là trung điểm của đoạn thẳng $AB$ và $M$ là điểm tùy ý. Chứng minh rằng: $\overrightarrow {MA} .\overrightarrow {MB} = I{M^2} – I{A^2}.$

Đẳng thức cần chứng minh được viết lại là $\overrightarrow {MA} .\overrightarrow {MB} = {\overrightarrow {IM} ^2} – {\overrightarrow {IA} ^2}.$
Để làm xuất hiện $\overrightarrow {IM} $, $\overrightarrow {IA} $ ở VP, sử dụng quy tắc ba điểm để xen điểm $I$ vào, ta được:
$VT = (\overrightarrow {MI} + \overrightarrow {IA} ).(\overrightarrow {MI} + \overrightarrow {IB} )$ $ = (\overrightarrow {MI} + \overrightarrow {IA} ).(\overrightarrow {MI} – \overrightarrow {IA} )$ $ = {\overrightarrow {IM} ^2} – {\overrightarrow {IA} ^2} = VP.$

Ví dụ 2: Cho bốn điểm $A$, $B$, $C$, $D$ bất kì. Chứng minh rằng:
$\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} = 0$ $(*).$
Từ đó suy ra một cách chứng minh định lí: “Ba đường cao trong tam giác đồng quy”.

Ta có: $\overrightarrow {DA} .\overrightarrow {BC} + \overrightarrow {DB} .\overrightarrow {CA} + \overrightarrow {DC} .\overrightarrow {AB} .$
$ = \overrightarrow {DA} .(\overrightarrow {DC} – \overrightarrow {DB} )$ $ + \overrightarrow {DB} .(\overrightarrow {DA} – \overrightarrow {DC} )$ $ + \overrightarrow {DC} .(\overrightarrow {DB} – \overrightarrow {DA} ).$
$ = \overrightarrow {DA} .\overrightarrow {DC} – \overrightarrow {DA} .\overrightarrow {DB} $ $ + \overrightarrow {DB} .\overrightarrow {DA} – \overrightarrow {DB} .\overrightarrow {DC} $ $ + \overrightarrow {DC} .\overrightarrow {DB} – \overrightarrow {DC} .\overrightarrow {DA} = 0.$
Gọi $H$ là giao của hai đường cao xuất phát từ đỉnh $A$, $B.$
Khi đó ta có: $\overrightarrow {HA} .\overrightarrow {BC} = 0$, $\overrightarrow {HC} .\overrightarrow {AB} = 0$ $(1).$
Từ đẳng thức $(*)$ ta cho điểm $D$ trùng với điểm $H$ ta được:
$\overrightarrow {HA} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {CA} + \overrightarrow {HC} .\overrightarrow {AB} = 0$ $(2).$
Từ $(1)$ và $(2)$ ta có $\overrightarrow {HB} .\overrightarrow {CA} = 0$ suy ra $BH$ vuông góc với $AC.$
Hay ba đường cao trong tam giác đồng quy.

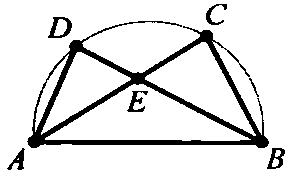
Ví dụ 3: Cho nửa đường tròn đường kính $AB.$ Có $AC$ và $BD$ là hai dây thuộc nửa đường tròn cắt nhau tại $E.$ Chứng minh rằng: $\overrightarrow {AE} .\overrightarrow {AC} + \overrightarrow {BE} .\overrightarrow {BD} = A{B^2}.$

Ta có $VT = \overrightarrow {AE} .(\overrightarrow {AB} + \overrightarrow {BC} )$ $ + \overrightarrow {BE} .(\overrightarrow {BA} + \overrightarrow {AD} ).$
$ = \overrightarrow {AE} .\overrightarrow {AB} + \overrightarrow {AE} .\overrightarrow {BC} $ $ + \overrightarrow {BE} .\overrightarrow {BA} + \overrightarrow {BE} .\overrightarrow {AD} .$
Vì $AB$ là đường kính nên $\widehat {ADB} = {90^0}$, $\widehat {ACB} = {90^0}.$
Suy ra $\overrightarrow {AE} .\overrightarrow {BC} = 0$, $\overrightarrow {BE} .\overrightarrow {AD} = 0.$
Do đó $VT = \overrightarrow {AE} .\overrightarrow {AB} + \overrightarrow {BE} .\overrightarrow {BA} $ $ = \overrightarrow {AB} (\overrightarrow {AE} + \overrightarrow {EB} )$ $ = {\overrightarrow {AB} ^2} = VP.$

Ví dụ 4: Cho tam giác $ABC$ có $BC = a$, $CA = b$, $AB = c$ và $I$ là tâm đường tròn nội tiếp. Chứng minh rằng $aI{A^2} + bI{B^2} + cI{C^2} = abc.$

Ta có: $a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} = \vec 0$ $ \Rightarrow {(a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} )^2} = 0.$
$ \Rightarrow {a^2}I{A^2} + {b^2}I{B^2} + {c^2}I{C^2}$ $ + 2ab\overrightarrow {IA} .\overrightarrow {IB} + 2bc\overrightarrow {IB} .\overrightarrow {IC} + 2ca\overrightarrow {IC} .\overrightarrow {IA} = 0.$
$ \Rightarrow {a^2}I{A^2} + {b^2}I{B^2} + {c^2}I{C^2}$ $ + ab\left( {I{A^2} + I{B^2} – A{B^2}} \right)$ $ + bc\left( {I{B^2} + I{C^2} – B{C^2}} \right)$ $ + ca\left( {I{A^2} + I{C^2} – C{A^2}} \right) = 0.$
$ \Rightarrow \left( {{a^2} + ab + ca} \right)I{A^2}$ $ + \left( {{b^2} + ba + bc} \right)I{B^2}$ $ + \left( {{c^2} + ca + cb} \right)I{C^2}$ $ – \left( {ab{c^2} + a{b^2}c + {a^2}bc} \right) = 0.$
$ \Rightarrow (a + b + c)\left( {{a^2}I{A^2} + {b^2}I{B^2} + {c^2}I{C^2}} \right)$ $ = (a + b + c)abc.$
$ \Rightarrow {a^2}I{A^2} + {b^2}I{B^2} + {c^2}I{C^2} = abc.$