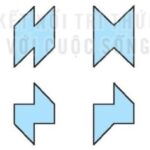
Bài: Ôn tập chương V - Giải SBT Toán lớp 6 - Sách Kết nối tri thức ============ Thuộc [Sách kết nối] Giải SBT Toán 6 ============= Câu 1: Trong các câu sau, câu nào đúng? A. Tam giác đều có 6 trục đối xứng B. Hình chữ nhật với hai kích thước khác nhau có 4 trục đối xứng C. Hình thang cân, góc ở đáy khác 90$^{o}$, có đúng một trục đối xứng; D. Hình bình hành có 2 … [Đọc thêm...] vềBài: Ôn tập chương V – Giải SBT Toán 6 – Sách Kết nối
Kết quả tìm kiếm cho: hình bình hành có 1 góc vuông
Bài: Ôn tập chương IV – Giải SBT Toán 6 – Sách Kết nối
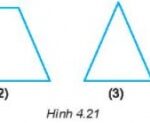
Bài: Ôn tập chương IV - Giải SBT Toán lớp 6 - Sách Kết nối tri thức ============ Thuộc [Sách kết nối] Giải SBT Toán 6 ============= Câu 1: Trong các hình dưới đây hình nào là hình thang cân? A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4 Câu 2: Trong các hình dưới đây hình nào là hình bình hành? A. Hình 1 B. Hình 2 … [Đọc thêm...] vềBài: Ôn tập chương IV – Giải SBT Toán 6 – Sách Kết nối
Bài 19: Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân – Toán lớp 6 (Tập 1) – Kết nối tri thức
Giải bài tập SGK Toán 6 - tập 1 - Sách Kết nối tri thức - Bài 19: Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân ============ Bài 19: Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân Chương ============= Hoạt động 1: Em hãy tìm một số hình ảnh của hình chữ nhật trong thực tế Lời giải: Một số hình ảnh của hình chữ nhật: cửa, ti vi, tủ lạnh, gạch … [Đọc thêm...] vềBài 19: Hình chữ nhật. Hình thoi. Hình bình hành. Hình thang cân – Toán lớp 6 (Tập 1) – Kết nối tri thức
29. Cho hình lăng trụ \(ABCD.A’B’C’D’\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = 120^\circ \). Hình chiếu của \(B’\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(CD\) và \(\Delta ABB’\) là tam giác vuông cân. Gọi \(\alpha \) là góc giữa hai đường thẳng \(BH\) và \(AC’\). Khi đó, \(\cos \alpha \) bằng
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 29. Cho hình lăng trụ \(ABCD.A'B'C'D'\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = 120^\circ \). Hình chiếu của \(B'\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(CD\) và \(\Delta ABB'\) là tam giác vuông cân. Gọi … [Đọc thêm...] về29. Cho hình lăng trụ \(ABCD.A’B’C’D’\) có đáy là hình thoi cạnh \(a\), \(\widehat {BAD} = 120^\circ \). Hình chiếu của \(B’\) lên mặt phẳng \(\left( {ABCD} \right)\) là trung điểm \(H\) của đoạn thẳng \(CD\) và \(\Delta ABB’\) là tam giác vuông cân. Gọi \(\alpha \) là góc giữa hai đường thẳng \(BH\) và \(AC’\). Khi đó, \(\cos \alpha \) bằng
8. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy và \(SA = a\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(BC\) và \(SD\), \(\alpha \) là góc giữa đường thẳng \(MN\) và mặt phẳng \(\left( {SAC} \right)\). Giá trị \(\tan \alpha \) là:
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 8. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy và \(SA = a\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(BC\) và \(SD\), \(\alpha \) là góc giữa đường thẳng \(MN\) và mặt phẳng \(\left( … [Đọc thêm...] về8. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh bên \(SA\) vuông góc với đáy và \(SA = a\). Gọi \(M,\,N\) lần lượt là trung điểm của các cạnh \(BC\) và \(SD\), \(\alpha \) là góc giữa đường thẳng \(MN\) và mặt phẳng \(\left( {SAC} \right)\). Giá trị \(\tan \alpha \) là:
13. Cho hình hộp \(ABCD.A’B’C’D’\) các điểm \(I,\,K\) thỏa mãn: \(\overrightarrow {ID’} + 2\overrightarrow {IA’} = \overrightarrow 0 \,\), \(\overrightarrow {KA} + 3\overrightarrow {KD} = \overrightarrow 0 \,\), \(E\) là giao điểm của \(CD’\) và \(C’D\), \(M\) là trung điểm của \(CD\). Tam giác \(ABC\) là tam giác đều cạnh \(a\), mặt phẳng \(\left( {IBD} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Diện tích tam giác \(IBD\) bằng \(6{a^2}\sqrt 3 \). Gọi \(G;\,G’\) lần lượt là trọng tâm tứ diện \(MBB’A’\) và \(\Delta AIE\). Khoảng cách giữa hai đường thẳng \(GG’\) và \(CK\) bằng
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 13. Cho hình hộp \(ABCD.A'B'C'D'\) các điểm \(I,\,K\) thỏa mãn: \(\overrightarrow {ID'} + 2\overrightarrow {IA'} = \overrightarrow 0 \,\), \(\overrightarrow {KA} + 3\overrightarrow {KD} = \overrightarrow 0 \,\), \(E\) là giao điểm … [Đọc thêm...] về13. Cho hình hộp \(ABCD.A’B’C’D’\) các điểm \(I,\,K\) thỏa mãn: \(\overrightarrow {ID’} + 2\overrightarrow {IA’} = \overrightarrow 0 \,\), \(\overrightarrow {KA} + 3\overrightarrow {KD} = \overrightarrow 0 \,\), \(E\) là giao điểm của \(CD’\) và \(C’D\), \(M\) là trung điểm của \(CD\). Tam giác \(ABC\) là tam giác đều cạnh \(a\), mặt phẳng \(\left( {IBD} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Diện tích tam giác \(IBD\) bằng \(6{a^2}\sqrt 3 \). Gọi \(G;\,G’\) lần lượt là trọng tâm tứ diện \(MBB’A’\) và \(\Delta AIE\). Khoảng cách giữa hai đường thẳng \(GG’\) và \(CK\) bằng
9. Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng đáy, \(ABCD\) là hình chữ nhật có \(AD = 3a,\,AC = 5a\), góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(45^\circ \). Khi đó \(\cos \) của góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( {SBC} \right)\) bằng
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 9. Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng đáy, \(ABCD\) là hình chữ nhật có \(AD = 3a,\,AC = 5a\), góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(45^\circ \). Khi đó \(\cos \) của góc giữa đường … [Đọc thêm...] về9. Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng đáy, \(ABCD\) là hình chữ nhật có \(AD = 3a,\,AC = 5a\), góc giữa hai mặt phẳng \(\left( {SCD} \right)\) và \(\left( {ABCD} \right)\) bằng \(45^\circ \). Khi đó \(\cos \) của góc giữa đường thẳng \(SD\) và mặt phẳng \(\left( {SBC} \right)\) bằng
25. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(\widehat {BAC} = 60^\circ ,\)tam giác \(SAB\) vuông tại \(S\), \(SA = a,\,SB = a\sqrt 3 \). Măt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(SC\). Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BM\).
DẠNG TOÁN TỔNG HỢP HÌNH HỌC KHÔNG GIAN - GÓC - KHOẢNG CÁCH - THỂ TÍCH - TỶ SỐ - CỰC TRỊ HÌNH HỌC =============== 25. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(\widehat {BAC} = 60^\circ ,\)tam giác \(SAB\) vuông tại \(S\), \(SA = a,\,SB = a\sqrt 3 \). Măt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(M\) là … [Đọc thêm...] về25. Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(\widehat {BAC} = 60^\circ ,\)tam giác \(SAB\) vuông tại \(S\), \(SA = a,\,SB = a\sqrt 3 \). Măt phẳng \(\left( {SAB} \right)\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Gọi \(M\) là trung điểm của \(SC\). Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BM\).
Bài tập ôn tập cuối năm – Toán lớp 6 (Tập 2) – Kết nối tri thức
Giải bài tập SGK Toán 6 - tập 2 - Sách Kết nối tri thức - Bài: Bài tập ôn tập cuối năm ============ Bài: Bài tập ôn tập cuối năm ============= Bài tập 1: Số tự nhiên n có sáu chữ số phân biệt , hai chữ số cạnh nhau luôn là hai số tự nhiên liên tiếp . Hãy tìm số n , biết rằng trong sáu chữ số của nó , chữ số 4 có giá trị bằng 4 000. Em tìm được mấy số như vậy ? Lời … [Đọc thêm...] vềBài tập ôn tập cuối năm – Toán lớp 6 (Tập 2) – Kết nối tri thức
Bài 2: Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân – Toán lớp 6 (Tập 1) – Chân trời sáng tạo
Giải bài tập SGK Toán 6 - tập 1 - Sách Chân trời sáng tạo - Bài 2: Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân ============ Bài 2: Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân Thuộc CHƯƠNG 3. HÌNH HỌC TRỰC QUAN. CÁC HÌNH PHẲNG TRONG THỰC TIỄN ============= A. GIẢI CÂU HỎI LUYỆN TẬP VÀ VẬN DỤNG Hoạt động 1: Trang 80 Toán 6 tập 1 sgk … [Đọc thêm...] vềBài 2: Hình chữ nhật – Hình thoi – Hình bình hành – Hình thang cân – Toán lớp 6 (Tập 1) – Chân trời sáng tạo