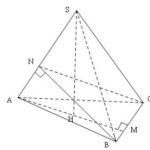
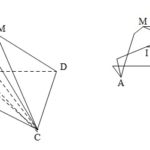
Đề bài: Cho hình chóp đều $S.ABC$ đỉnh $S$ có các cạnh đáy đều bằng $a$, đường cao hình chóp $SH = h.$$a$) Xác định thiết diện tạo bởi hình chóp với mặt phẳng ($P$) qua cạnh đáy $BC$ và vuông góc với cạnh bên $SA.$$b)$ Nếu tỉ số $\frac{h}{a} = \sqrt 3 $ thì mặt phẳng ($P$) chia thể tích hình chóp theo tỉ số nào? Lời giải $a$. Vì $SABC$ là hình chóp đều nên chân … [Đọc thêm...] vềĐề bài: Cho hình chóp đều $S.ABC$ đỉnh $S$ có các cạnh đáy đều bằng $a$, đường cao hình chóp $SH = h.$$a$) Xác định thiết diện tạo bởi hình chóp với mặt phẳng ($P$) qua cạnh đáy $BC$ và vuông góc với cạnh bên $SA.$$b)$ Nếu tỉ số $\frac{h}{a} = \sqrt 3 $ thì mặt phẳng ($P$) chia thể tích hình chóp theo tỉ số nào?
Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ vuông góc nhau từng đôi một, với $OA=a, OB=b$. Gọi $M$ là trung điểm $BC$. Xác định và tính đoạn vuông góc của $OC$ và $AM$.
Đề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ vuông góc nhau từng đôi một, với $OA=a, OB=b$. Gọi $M$ là trung điểm $BC$. Xác định và tính đoạn vuông góc của $OC$ và $AM$. Lời giải vẽ $MM' \parallel OC (M'\in OB)$, ta có: $OC \parallel (AM'M).$Vẽ $OH\bot AM'$, suy ra $OH\bot (AMM')$.Vẽ $HI \parallel OC(I\in AM)$ và $IJ \parallel OH(J\in OC)$, ta có $IJ$ là đoạn vuông … [Đọc thêm...] vềĐề bài: Cho tứ diện $OABC$ có $OA, OB, OC$ vuông góc nhau từng đôi một, với $OA=a, OB=b$. Gọi $M$ là trung điểm $BC$. Xác định và tính đoạn vuông góc của $OC$ và $AM$.
Đề bài: Cho hai tam giác $ABC,A'B'C'$ nằm trong hai mặt phẳng phân biệt.Chứng minh rằng các đường thẳng đi qua các trung điểm của các cặp cạnh $AB'$ và $A'B,BC'$ và $B'C,CA'$ và $C'A$ song song với một mặt phẳng
Đề bài: Cho hai tam giác $ABC,A'B'C'$ nằm trong hai mặt phẳng phân biệt.Chứng minh rằng các đường thẳng đi qua các trung điểm của các cặp cạnh $AB'$ và $A'B,BC'$ và $B'C,CA'$ và $C'A$ song song với một mặt phẳng Lời giải Đặt $\overrightarrow {a},\overrightarrow {b},\overrightarrow {c} $ là các véctơ chỉ phương của các … [Đọc thêm...] vềĐề bài: Cho hai tam giác $ABC,A'B'C'$ nằm trong hai mặt phẳng phân biệt.Chứng minh rằng các đường thẳng đi qua các trung điểm của các cặp cạnh $AB'$ và $A'B,BC'$ và $B'C,CA'$ và $C'A$ song song với một mặt phẳng
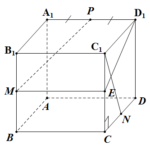
Đề bài: Cho hình lập phương $ABCD. A_1B_1C_1D_1$. Gọi $M,N,P$ lần lượt là trung điểm của $BB_1, CD, A_1D_1$. Chứng minh $MP \bot C_1N$.
Đề bài: Cho hình lập phương $ABCD. A_1B_1C_1D_1$. Gọi $M,N,P$ lần lượt là trung điểm của $BB_1, CD, A_1D_1$. Chứng minh $MP \bot C_1N$. Lời giải Gọi $E$ là trung điểm của $CC_1$.ta có: $ME// BC\Rightarrow ME// A_1D_1$.Gọi $(Q)$ là mặt phẳng $MED_1A_1\Rightarrow MP \in (Q) (1)$Dễ thấy hai tam giác vuông $C_1CN; D_1C_1E$ bằng nhau $\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD. A_1B_1C_1D_1$. Gọi $M,N,P$ lần lượt là trung điểm của $BB_1, CD, A_1D_1$. Chứng minh $MP \bot C_1N$.
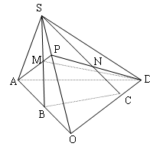
Đề bài: Trong mặt phẳng $\alpha$ cho tứ giác $ABCD$ có $AB$ và $CD$ không song song.$S$ là một điểm không thuộc $\alpha,M$ là điểm di động trên cạnh $SB$. Mặt phẳng $(ADM)$ cắt $SC$ tại $N$. Tìm tập hợp giao điểm của $AM,DN$
Đề bài: Trong mặt phẳng $\alpha$ cho tứ giác $ABCD$ có $AB$ và $CD$ không song song.$S$ là một điểm không thuộc $\alpha,M$ là điểm di động trên cạnh $SB$. Mặt phẳng $(ADM)$ cắt $SC$ tại $N$. Tìm tập hợp giao điểm của $AM,DN$ Lời giải *Phần thuận Ta có :$AM\subset (SAB)$- cố địnhMặt khác, vì $DN$ đi qua điểm cố định $D$ và cắt đường thẳng cố định $SC$ nên … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $\alpha$ cho tứ giác $ABCD$ có $AB$ và $CD$ không song song.$S$ là một điểm không thuộc $\alpha,M$ là điểm di động trên cạnh $SB$. Mặt phẳng $(ADM)$ cắt $SC$ tại $N$. Tìm tập hợp giao điểm của $AM,DN$
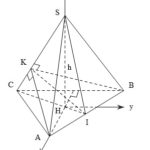
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông; $SA\bot (ABCD)$.Qua $A$ dựng thiết diện vuông góc với $SC$ cắt $SC,SB,SD$ theo thứ tự tại $K,E,H$$a.$ Chứng minh $AE\bot SB,AH\bot SD$$b.$ Chứng minh tứ giác $AEKH$ nội tiếp được và có hai đường chéo vuông góc với nhau
Đề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông; $SA\bot (ABCD)$.Qua $A$ dựng thiết diện vuông góc với $SC$ cắt $SC,SB,SD$ theo thứ tự tại $K,E,H$$a.$ Chứng minh $AE\bot SB,AH\bot SD$$b.$ Chứng minh tứ giác $AEKH$ nội tiếp được và có hai đường chéo vuông góc với nhau Lời giải $a.$ Ta có$\left.\begin{matrix}SA\bot (ABCD) \\BC\bot AB \end{matrix}\right\} … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ đáy $ABCD$ là hình vuông; $SA\bot (ABCD)$.Qua $A$ dựng thiết diện vuông góc với $SC$ cắt $SC,SB,SD$ theo thứ tự tại $K,E,H$$a.$ Chứng minh $AE\bot SB,AH\bot SD$$b.$ Chứng minh tứ giác $AEKH$ nội tiếp được và có hai đường chéo vuông góc với nhau
Đề bài: Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy là $a$, đường cao $SH=h$. Mặt phẳng $(\alpha )$ qua $AB$ và $(\alpha )\bot SC$a) Tìm điều kiện của $h$ để $(\alpha )$ cắt cạnh $SC$ tại $K$. Tính diện tích $\Delta ABK$b) Tính $h$ theo $a$ để $(\alpha )$ chia hình chóp theo hai phần có thể tích bằng nhau. Chứng tỏ khi đó tâm mặt cầu nội tiếp và ngoại tiếp trùng nhau
Đề bài: Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy là $a$, đường cao $SH=h$. Mặt phẳng $(\alpha )$ qua $AB$ và $(\alpha )\bot SC$a) Tìm điều kiện của $h$ để $(\alpha )$ cắt cạnh $SC$ tại $K$. Tính diện tích $\Delta ABK$b) Tính $h$ theo $a$ để $(\alpha )$ chia hình chóp theo hai phần có thể tích bằng nhau. Chứng tỏ khi đó tâm mặt cầu nội tiếp và ngoại tiếp trùng nhau … [Đọc thêm...] vềĐề bài: Cho hình chóp tam giác đều $S.ABC$ có cạnh đáy là $a$, đường cao $SH=h$. Mặt phẳng $(\alpha )$ qua $AB$ và $(\alpha )\bot SC$a) Tìm điều kiện của $h$ để $(\alpha )$ cắt cạnh $SC$ tại $K$. Tính diện tích $\Delta ABK$b) Tính $h$ theo $a$ để $(\alpha )$ chia hình chóp theo hai phần có thể tích bằng nhau. Chứng tỏ khi đó tâm mặt cầu nội tiếp và ngoại tiếp trùng nhau
Đề bài: Trên các cạnh $AD$ và $BD$ của tứ diện $ABCD$ lấy các điểm $M, N$ sao cho $\frac{AM}{AD}=\frac{BN}{BD}=m$. Tìm khoảng cách giữa các trọng tâm tam giác $\Delta ACN$ và $\Delta BMC$ theo $AB=a$.
Đề bài: Trên các cạnh $AD$ và $BD$ của tứ diện $ABCD$ lấy các điểm $M, N$ sao cho $\frac{AM}{AD}=\frac{BN}{BD}=m$. Tìm khoảng cách giữa các trọng tâm tam giác $\Delta ACN$ và $\Delta BMC$ theo $AB=a$. Lời giải Từ giả thiết cho: $\frac{DM}{AD}=\frac{DN}{DB}=\frac{MN}{AB}\Leftrightarrow \frac{DA-AM}{DA}=\frac{MN}{a}$$\Leftrightarrow … [Đọc thêm...] vềĐề bài: Trên các cạnh $AD$ và $BD$ của tứ diện $ABCD$ lấy các điểm $M, N$ sao cho $\frac{AM}{AD}=\frac{BN}{BD}=m$. Tìm khoảng cách giữa các trọng tâm tam giác $\Delta ACN$ và $\Delta BMC$ theo $AB=a$.
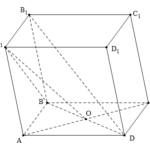
Đề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ lên mặt phẳng $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1), (ABCD)$ tạo với nhau góc $60^0$. Tìm khoảng cách từ $ B_1$ đến mặt phẳng $(A_1BD)$.
Đề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ lên mặt phẳng $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1), (ABCD)$ tạo với nhau góc $60^0$. Tìm khoảng cách từ $ B_1$ đến mặt phẳng $(A_1BD)$. Lời giải Ta có … [Đọc thêm...] vềĐề bài: Cho hình lăng trụ $ABCD.A_1B_1C_1D_1$ có đáy $ABCD$ là hình chữ nhật với $AB=a, AD=a\sqrt{3}$. Hình chiếu vuông góc của $A_1$ lên mặt phẳng $(ABCD)$ trùng với giao điểm $O$ của hai đường chéo $AC,BD$ của đáy. Biết rằng hai mặt phẳng $(ADD_1A_1), (ABCD)$ tạo với nhau góc $60^0$. Tìm khoảng cách từ $ B_1$ đến mặt phẳng $(A_1BD)$.
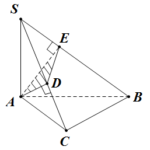
Đề bài: Cho hình chóp $S.ABC$, trong đó đáy $ABC$ là tam giác vuông tại $C$, hai mặt bên $(SAC),(SAB)$ cùng vuông góc với đáy $ABC$. Gọi $D,E$ lần lượt là hình chiếu của $A$ trên $SC,SB$. Chứng minh $(SAB) \bot (ADE)$
Đề bài: Cho hình chóp $S.ABC$, trong đó đáy $ABC$ là tam giác vuông tại $C$, hai mặt bên $(SAC),(SAB)$ cùng vuông góc với đáy $ABC$. Gọi $D,E$ lần lượt là hình chiếu của $A$ trên $SC,SB$. Chứng minh $(SAB) \bot (ADE)$ Lời giải Vì $(SAB) \bot (ABC); (SAC) \bot (ABC)$,mà $(SAB) \cap (SAC)=SA$, nên $SA \bot (ABC)$.Vì $BC \bot CA \Rightarrow BC \bot (SAC)$.$\Rightarrow … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABC$, trong đó đáy $ABC$ là tam giác vuông tại $C$, hai mặt bên $(SAC),(SAB)$ cùng vuông góc với đáy $ABC$. Gọi $D,E$ lần lượt là hình chiếu của $A$ trên $SC,SB$. Chứng minh $(SAB) \bot (ADE)$