Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

BỒI DƯỠNG HỌC SINH GIỎI HÌNH KHÔNG GIAN

Ngày Thuộc chủ đề:Sách toán 12 Tag với:

BỒI DƯỠNG HỌC SINH GIỎI HÌNH KHÔNG GIAN TẠP CHÍ VÀ TƯ LIỆU TOÁN HỌC CHINH PHỤC OLYMPIC TOÁN HÌNH KHÔNG GIAN Sưu tầm và tổng hợp Phương pháp Vector không gian bồi dưỡng học sinh giỏi – Nhóm Toán Bắc TrungNam.[3]. Tài liệu tham khảo trên Internet.Chuyên đề cực trị hình học không gian – Strong Team Toán VD – VDC. =================== … [Đọc thêm...] vềBỒI DƯỠNG HỌC SINH GIỎI HÌNH KHÔNG GIAN

THỂ TÍCH TRONG PHÂN CHIA KHỐI ĐA DIỆN

Ngày Thuộc chủ đề:Sách toán 12 Tag với:,

THỂ TÍCH TRONG PHÂN CHIA KHỐI ĐA DIỆN Trong các bài toán thể tích khối đa diện diện , một số bài toán vận dụng hoặc vận dụng cao thườngđề cập đến việc phân chia đa diện , tính thể tích khối đa diện mới theo thể tích khối đa diện đã cho. Thầy cô cần tạo tình huống cho học trò có tư duy về việc so sánh thể tích các khối chóp , khối lăngtrụ từ những tư duy đơn giản như so … [Đọc thêm...] vềTHỂ TÍCH TRONG PHÂN CHIA KHỐI ĐA DIỆN

Tuyển chọn đề thi học sinh Giỏi môn Toán THPT 2020

Ngày Thuộc chủ đề:Đề thi toán Tag với:,

Tuyển chọn đề thi học sinh Giỏi THPT 2020 toàn quốc TUYỂN CHỌN ĐỀ THI HỌC SINH GIỎI TOÀN QUỐC 2020 MÔN TOÁN THPT Chỉ có một mục đích duy nhất là sưu tầm các đề thi học sinh giỏi toàn quốc thành mộttài liệu chuẩn mực để có thể dùng cho việc giảng dạy, cho các em học sinh tham khảo. Tôi đãtổng hợp thành tài liệu này. Tài liệu có 3 tập, mỗi tập khoảng 130 – 150 … [Đọc thêm...] vềTuyển chọn đề thi học sinh Giỏi môn Toán THPT 2020

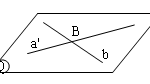
Đề bài: Giả sử $a$ và $b$ là hai đường chéo nhau. Chứng minh rằng tồn tại duy nhất một mặt phẳng $(P)$ chứa $a$ và một mặt phẳng $(Q)$ chứa $b$ sao cho $(P)//(Q)$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Giả sử $a$ và $b$ là hai đường chéo nhau. Chứng minh rằng tồn tại duy nhất một mặt phẳng $(P)$ chứa $a$ và một mặt phẳng $(Q)$ chứa $b$ sao cho $(P)//(Q)$ Lời giải   Qua một điểm $A\in a$, vẽ đường thẳng $b'$ song song với $b$ và qua một điểm $B\in b$ vẽ đường thẳng $a'$ song song với $a$. Gọi $(P)$= mp$(a,b')$, $(Q)$= mp$(b,a')$ thì rõ ràng $(P)\parallel … [Đọc thêm...] vềĐề bài: Giả sử $a$ và $b$ là hai đường chéo nhau. Chứng minh rằng tồn tại duy nhất một mặt phẳng $(P)$ chứa $a$ và một mặt phẳng $(Q)$ chứa $b$ sao cho $(P)//(Q)$

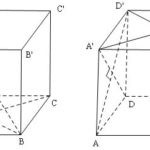
Đề bài: Cho hình lập phương $ABCD.A’B’C’D’$ với cạnh bằng $a$.$1.$ Hãy tính khoảng cách giữa hai đường thẳng $AA’$ và $BD’$$2.$ Chứng minh rằng đường chéo $BD’$ vuông góc với mặt phẳng $(DA’C’).$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lập phương $ABCD.A’B’C’D’$ với cạnh bằng $a$.$1.$ Hãy tính khoảng cách giữa hai đường thẳng $AA’$ và $BD’$$2.$ Chứng minh rằng đường chéo $BD’$ vuông góc với mặt phẳng $(DA’C’).$ Lời giải $1.$ Gọi $I, J$ lần lượt là trung điểm của $AA’, BD’$. Dễ thấy $IJ$ là chân đường vuông góc chung của $AA’$ và $BD’$. Vậy khoảng cách cần tính chính là đoạn $IJ$. … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A’B’C’D’$ với cạnh bằng $a$.$1.$ Hãy tính khoảng cách giữa hai đường thẳng $AA’$ và $BD’$$2.$ Chứng minh rằng đường chéo $BD’$ vuông góc với mặt phẳng $(DA’C’).$

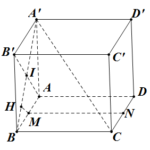
Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tìm khoảng cách giữa hai đường thẳng $A'C, MN$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tìm khoảng cách giữa hai đường thẳng $A'C, MN$. Lời giải Ta có $BC//MN\Rightarrow MN//(A'BC) \Rightarrow d(MN,A'C)=d(M,(A'BC))=d(M,(A'BC))  (1)$Ta có: $AI \bot A'B (A'B \cap AB'=I)$.Ta lại có: $ BC \bot   (BAA'B) \Rightarrow BC \bot … [Đọc thêm...] vềĐề bài: Cho hình lập phương $ABCD.A'B'C'D'$ cạnh bằng $1$. Gọi $M,N$ lần lượt là trung điểm của $AB,CD$. Tìm khoảng cách giữa hai đường thẳng $A'C, MN$.

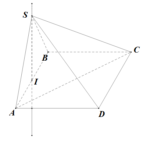
Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Qua trung điểm $I$ của cạnh $AB$ dựng đường thẳng $d$ vuông góc với mặt phẳng $(ABCD)$. Trên $d$ lấy điểm $S$ sao cho $SI=\frac{a\sqrt{3}}{2}$.1) Tìm thể tích hình chóp $S.ACD$.2) Tìm khoảng cách từ $C$ đến $(SAD)$.

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Qua trung điểm $I$ của cạnh $AB$ dựng đường thẳng $d$ vuông góc với mặt phẳng $(ABCD)$. Trên $d$ lấy điểm $S$ sao cho $SI=\frac{a\sqrt{3}}{2}$.1) Tìm thể tích hình chóp $S.ACD$.2) Tìm khoảng cách từ $C$ đến $(SAD)$. Lời giải 1) … [Đọc thêm...] vềĐề bài: Trong mặt phẳng $(P)$ cho hình vuông $ABCD$ cạnh bằng $a$. Qua trung điểm $I$ của cạnh $AB$ dựng đường thẳng $d$ vuông góc với mặt phẳng $(ABCD)$. Trên $d$ lấy điểm $S$ sao cho $SI=\frac{a\sqrt{3}}{2}$.1) Tìm thể tích hình chóp $S.ACD$.2) Tìm khoảng cách từ $C$ đến $(SAD)$.