Đề bài: Cho $f(x)$ là hàm số thực, xác định, liên tục trên đoạn $\left[ {0;\frac{\pi }{2}} \right]$, có $f(0) > 0$ và$\int\limits_0^{\frac{\pi }{2}} {f(x)dx < 1} $. Chứng minh rằng, phương trình $f(x) = sinx$ có ít nhất một nghiệm trên đoạn $\left[ {0;\frac{\pi }{2}} \right]$ Lời giải Xét $F(x)=f(x)-sinx$.Từ giả thiết, $F(x)$ liên tục trên $[0,\frac{\pi}{2} … [Đọc thêm...] vềĐề: Cho $f(x)$ là hàm số thực, xác định, liên tục trên đoạn $\left[ {0;\frac{\pi }{2}} \right]$, có $f(0) > 0$ và$\int\limits_0^{\frac{\pi }{2}} {f(x)dx < 1} $. Chứng minh rằng, phương trình $f(x) = sinx$ có ít nhất một nghiệm trên đoạn $\left[ {0;\frac{\pi }{2}} \right]$
Bài tập Hàm số
Đề: Cho hàm số:$y = – {x^3} + 3{x^2} – 2\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số.$2$.Tìm các điểm thuộc đồ thị ($C$) mà qua đó kẻ được một và chỉ một tiếp tuyến với đồ thị $(C)$
Đề bài: Cho hàm số:$y = - {x^3} + 3{x^2} - 2\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số.$2$.Tìm các điểm thuộc đồ thị ($C$) mà qua đó kẻ được một và chỉ một tiếp tuyến với đồ thị $(C)$ Lời giải $1.$ Bạn đọc tự giải$2.$ Xét $A(x_0,y_0=-x_0^3+3x_0^2-2)\in (C)$ Đường thẳng đi qua $A$ với hệ số góc $k$ có phương trình :$y=k(x-x_0)-x_0^3+3x_0^2-2$. … [Đọc thêm...] vềĐề: Cho hàm số:$y = – {x^3} + 3{x^2} – 2\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị ($C$) của hàm số.$2$.Tìm các điểm thuộc đồ thị ($C$) mà qua đó kẻ được một và chỉ một tiếp tuyến với đồ thị $(C)$
Đề: Tìm miền xác định của các hàm số:$a) y = log_3(x + 2); b) y = log(x+1)^2$$c) y = lo{g_2}\frac{{1 – x}}{{1 + x}}; d) y = log(x^2 + 3x +2)$
Đề bài: Tìm miền xác định của các hàm số:$a) y = log_3(x + 2); b) y = log(x+1)^2$$c) y = lo{g_2}\frac{{1 - x}}{{1 + x}}; d) y = log(x^2 + 3x +2)$ Lời giải $a)$ Hàm số $y = log_3 (x +2)$ có nghĩa khi $x + 2 > 0 \Leftrightarrow x > - 2$$ \Rightarrow $ Miền xác định của hàm số đó là $D =( -2, + \infty $)$b) y = log(x+1)^2$ có nghĩa khi: $x + 1 \neq 0 … [Đọc thêm...] vềĐề: Tìm miền xác định của các hàm số:$a) y = log_3(x + 2); b) y = log(x+1)^2$$c) y = lo{g_2}\frac{{1 – x}}{{1 + x}}; d) y = log(x^2 + 3x +2)$
Đề: Cho hàm số \(f(x)=\begin{cases}\frac{x^{3}-1}{x-1}, x\neq 1 \\ 3, x=1\end{cases}\). Chứng minh rằng \(f(x)\) liên tục tại \(x=1\).
Đề bài: Cho hàm số \(f(x)=\begin{cases}\frac{x^{3}-1}{x-1}, x\neq 1 \\ 3, x=1\end{cases}\). Chứng minh rằng \(f(x)\) liên tục tại \(x=1\). Lời giải \(\mathop {\lim }\limits_{x \to1^{-}}f(x)= \mathop {\lim }\limits_{x \to1^{-}}\frac{x^3-1}{x-1}= \mathop {\lim }\limits_{x \to1^{-}} (x^{2}+x+1)=3= \mathop {\lim }\limits_{x \to1^{+}} f(x) \)\(\Rightarrow \mathop {\lim … [Đọc thêm...] vềĐề: Cho hàm số \(f(x)=\begin{cases}\frac{x^{3}-1}{x-1}, x\neq 1 \\ 3, x=1\end{cases}\). Chứng minh rằng \(f(x)\) liên tục tại \(x=1\).
Đề: Chứng minh rằng các phương trình sau đây:1) \(x^{5}-3x-1=0\) có ít nhất 1 nghiệm \(1
Đề bài: Chứng minh rằng các phương trình sau đây:1) \(x^{5}-3x-1=0\) có ít nhất 1 nghiệm \(1 Lời giải 1) Hàm số \(f(x)=x^{5}-3x-1\) liên tục trên đoạn \([1,2]\)Lại biết \(f(1)f(2)=(1-3-1)(32-6-1)Suy ra đoạn đồ thị hàm số đã cho từ (1;2) cắt trục Ox.Vậy phương trình \(x^{5}-3x-1=0\) có ít nhất 1 nghiệm \(12) Hàm số \(f(x)=x.2^{x}-1\) liên tục trên đoạn \([0,1]\)Biết … [Đọc thêm...] vềĐề: Chứng minh rằng các phương trình sau đây:1) \(x^{5}-3x-1=0\) có ít nhất 1 nghiệm \(1
Đề: Cho đường tròn $(C):$$(x-2)^2+(y-3)^2=5$a. Xác định phương trình tham số của $(C)$b. Tìm trên $(C)$ điểm $M$ sao cho $MA$ đạt giá trị lớn nhất, nhỏ nhất biết rằng $A(4;-1)$
Đề bài: Cho đường tròn $(C):$$(x-2)^2+(y-3)^2=5$a. Xác định phương trình tham số của $(C)$b. Tìm trên $(C)$ điểm $M$ sao cho $MA$ đạt giá trị lớn nhất, nhỏ nhất biết rằng $A(4;-1)$ Lời giải a. Đường tròn $(C)$ tâm $I(2;3)$, bán kính $R=\sqrt{5} $ có phương trình tham số là:$(C):\left\{ \begin{array}{l} x=2+\sqrt{5}\sin t \\ y=3+\sqrt{5}\cos t \end{array} \right. … [Đọc thêm...] vềĐề: Cho đường tròn $(C):$$(x-2)^2+(y-3)^2=5$a. Xác định phương trình tham số của $(C)$b. Tìm trên $(C)$ điểm $M$ sao cho $MA$ đạt giá trị lớn nhất, nhỏ nhất biết rằng $A(4;-1)$
Đề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2}}}{{x – 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\).
Đề bài: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2}}}{{x - 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\). Lời giải $1$. Bạn đọc tự giải:$2$. Đường thẳng $y = 4$ tiếp xúc với $(C)$ tại điểm $(2, 4)$. Các điểm cần tìm là các giao … [Đọc thêm...] vềĐề: $1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2}}}{{x – 1}}\left( C \right)\)$2$. Tìm trên đường thẳng $y = 4$ tất cả các điểm mà từ mỗi điểm đó có thể kẻ tới đồ thị $(C)$ hai tiếp tuyến lập với nhau $1$ góc \({45^0}\).
Đề: Cho hàm số \(y = {x^3} – 3{x^2} + 3mx + 3m + 4\,\,\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =1$$2$. Hãy xác định giá trị của $m$ để đường cong \(\left( {{C_m}} \right)\) nhân điểm $I(1, 2)$ làm điểm uốn$3$. Với những giá trị nào của $m$ thì đường cong \(\left( {{C_m}} \right)\) tiếp xúc với trục hoành.
Đề bài: Cho hàm số \(y = {x^3} - 3{x^2} + 3mx + 3m + 4\,\,\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =1$$2$. Hãy xác định giá trị của $m$ để đường cong \(\left( {{C_m}} \right)\) nhân điểm $I(1, 2)$ làm điểm uốn$3$. Với những giá trị nào của $m$ thì đường cong \(\left( {{C_m}} \right)\) tiếp xúc với trục hoành. Lời giải $1$. Bạn đọc tự … [Đọc thêm...] vềĐề: Cho hàm số \(y = {x^3} – 3{x^2} + 3mx + 3m + 4\,\,\left( {{C_m}} \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số khi $m =1$$2$. Hãy xác định giá trị của $m$ để đường cong \(\left( {{C_m}} \right)\) nhân điểm $I(1, 2)$ làm điểm uốn$3$. Với những giá trị nào của $m$ thì đường cong \(\left( {{C_m}} \right)\) tiếp xúc với trục hoành.
Đề: Cho $x, y$ là hai số thay đổi thỏa mãn điều kiện: $0 \le x \le 3,0 \le y \le 4$.Tìm giá trị lớn nhất của biểu thức: $A = (3 – x)(4 – y)(2x + 3y)$
Đề bài: Cho $x, y$ là hai số thay đổi thỏa mãn điều kiện: $0 \le x \le 3,0 \le y \le 4$.Tìm giá trị lớn nhất của biểu thức: $A = (3 - x)(4 - y)(2x + 3y)$ Lời giải Ta có: $6A = (6 - 2x)(12 - 3y)(2x + 3y)$Theo giả thiết ta có $6 - 2x \ge 0,{\rm{ 12}} - 3y \ge 0,{\rm{ 2x}} + 3y \ge 0$Do đó áp dụng bất đẳng thức Côsi cho ba số không âm ta được:$6A \le {\left[ {\frac{{(6 - … [Đọc thêm...] vềĐề: Cho $x, y$ là hai số thay đổi thỏa mãn điều kiện: $0 \le x \le 3,0 \le y \le 4$.Tìm giá trị lớn nhất của biểu thức: $A = (3 – x)(4 – y)(2x + 3y)$
Đề: a) Tìm các khoảng đơn điệu của hàm số $y=x \ln^2 x.$b) Tìm điểm cực trị của hàm số $y=f(x)=x^2\ln x.$
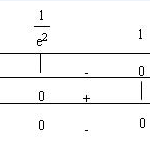
Đề bài: a) Tìm các khoảng đơn điệu của hàm số $y=x \ln^2 x.$b) Tìm điểm cực trị của hàm số $y=f(x)=x^2\ln x.$ Lời giải a) Hàm số $y=x \ln^2 x$ có tập xác định $D=(0;+\infty)$ Ta có $y'=\ln x (\ln x+2)$. Do đó $ y'=0\Leftrightarrow \left[ \begin{array}{l}\ln x=0\\\ln x=-2\end{array} \right.\Leftrightarrow \left[ \begin{array}{l}x=1\\x=\frac{1}{e^2} \end{array} \right.$Vậy … [Đọc thêm...] vềĐề: a) Tìm các khoảng đơn điệu của hàm số $y=x \ln^2 x.$b) Tìm điểm cực trị của hàm số $y=f(x)=x^2\ln x.$