Đề bài: Tính đạo hàm các hàm số sau đây:a) $y=\sin 3x-\cos3x$ b) $y=\frac {x}{\sin x}$ c) $y=\sin ^32x$ d) $y= \cos \frac{1}{x}$ Lời giải Ta có:a) $y'=(\sin3x)'-(\cos3x)'=3\cos3x+3\sin3x$.b) $y'=\frac{\sin x(x)'-(\sin x)'.x}{\sin^2x}=\frac{\sin x -x\cos x}{\sin^2x}$ .c) $y'=3\sin^22x(\sin2x)'=6\sin^22x\cos2x$ .d) $y'= … [Đọc thêm...] vềĐề: Tính đạo hàm các hàm số sau đây:a) $y=\sin 3x-\cos3x$ b) $y=\frac {x}{\sin x}$ c) $y=\sin ^32x$ d) $y= \cos \frac{1}{x}$
Bài tập Hàm số
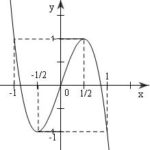
Đề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$
Đề bài: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x - 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 - 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$ Lời giải 1. Khảo sát , đồ thị (xin dành cho bạn đọc). Từ đồ thị hàm số: $y = 3x - 4{x^3}$ta suy ra đồ thị hàm số $y = |x|\left( {3 - 4{x^2}} … [Đọc thêm...] vềĐề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị hàm số: $y = 3x – 4x^3$Từ đó suy ra đồ thị của hàm số: $y = |x|\left( {3 – 4{x^2}} \right)$$2.$ Viết phương trình tiếp tuyến với ($C$) đi qua $A(1;3).$
Đề: Tìm tập xác định của hàm số:$y = {2^{\sqrt {\left| {X – 3} \right| – \left| {8 – X} \right|} }} + {\sqrt {\frac{{ – {{\log }_{0,3}}(X – 1)}}{{\sqrt {{X^2} – 2X – 8} }}} _{}}$ĐH Y Hà Nội 1997
Đề bài: Tìm tập xác định của hàm số:$y = {2^{\sqrt {\left| {X - 3} \right| - \left| {8 - X} \right|} }} + {\sqrt {\frac{{ - {{\log }_{0,3}}(X - 1)}}{{\sqrt {{X^2} - 2X - 8} }}} _{}}$ĐH Y Hà Nội 1997 Lời giải … [Đọc thêm...] vềĐề: Tìm tập xác định của hàm số:$y = {2^{\sqrt {\left| {X – 3} \right| – \left| {8 – X} \right|} }} + {\sqrt {\frac{{ – {{\log }_{0,3}}(X – 1)}}{{\sqrt {{X^2} – 2X – 8} }}} _{}}$ĐH Y Hà Nội 1997
Đề: Cho hàm số $ y_k=\frac{2k\cos x+k+1}{\cos x+\sin x+2}$a) Tìm giá trị lớn nhất và giá trị nhỏ nhất với $y_1$ ( ứng với $k=1$)b) Tìm $k$ để giá trị lớn nhất của $y_k$ là nhỏ nhất.
Đề bài: Cho hàm số $ y_k=\frac{2k\cos x+k+1}{\cos x+\sin x+2}$a) Tìm giá trị lớn nhất và giá trị nhỏ nhất với $y_1$ ( ứng với $k=1$)b) Tìm $k$ để giá trị lớn nhất của $y_k$ là nhỏ nhất. Lời giải Miền xác định : $ D=R$ ( vì $ \cos x+\sin x+2=\sqrt{2}\left ( \sqrt{2}+\sin (x+\frac{\pi}{4}) \right )>0, \forall x \in R$)Khi đó: $(y_k-2k)\cos x+y_k\sin 2x=k+1-2y_k$Điều kiện … [Đọc thêm...] vềĐề: Cho hàm số $ y_k=\frac{2k\cos x+k+1}{\cos x+\sin x+2}$a) Tìm giá trị lớn nhất và giá trị nhỏ nhất với $y_1$ ( ứng với $k=1$)b) Tìm $k$ để giá trị lớn nhất của $y_k$ là nhỏ nhất.
Đề: Cho hàm số $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1) Với giá trị nào của $m$ thì hàm số có cực trị?2) Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3) Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$
Đề bài: Cho hàm số $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1) Với giá trị nào của $m$ thì hàm số có cực trị?2) Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3) Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$ Lời giải $1)$ Ta có $y = x + 2{m^2} - 1 + \frac{{1 - {m^2}}}{{x + 1}}$, do đó$y' = 1 - \frac{{1 - … [Đọc thêm...] vềĐề: Cho hàm số $y = \frac{{{x^2} + 2{m^2}x + {m^2}}}{{x + 1}}$1) Với giá trị nào của $m$ thì hàm số có cực trị?2) Xác định $m$ để đồ thị của hàm số có 2 điểm đối xứng với nhau qua gốc tọa độ.3) Khảo sát sự biến thiên và vẽ đồ thị ứng với $m = 2$
Đề: Cho hàm số \(y = \frac{{{x^2} – x + 1}}{{x – 1}}\)$1$. Khảo sát hàm số đã cho$2$. Xác định điểm \(A\left( {{x_1},{y_1}} \right)\) thuộc đồ thị của hàm số trên sao cho khoảng cách từ $A$ đến giao điểm của hai tiệm cận là nhỏ nhất.
Đề bài: Cho hàm số \(y = \frac{{{x^2} - x + 1}}{{x - 1}}\)$1$. Khảo sát hàm số đã cho$2$. Xác định điểm \(A\left( {{x_1},{y_1}} \right)\) thuộc đồ thị của hàm số trên sao cho khoảng cách từ $A$ đến giao điểm của hai tiệm cận là nhỏ nhất. Lời giải $1$. Bạn đọc tự giải$2$. Giao điểm hai tiệm cận là $E (1, 1)$. Xét điểm \(A\left( {{x_1},{y_1}} \right)\) với \({x_1} > 1\)$A$ … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} – x + 1}}{{x – 1}}\)$1$. Khảo sát hàm số đã cho$2$. Xác định điểm \(A\left( {{x_1},{y_1}} \right)\) thuộc đồ thị của hàm số trên sao cho khoảng cách từ $A$ đến giao điểm của hai tiệm cận là nhỏ nhất.
Đề: a) Cho $x,y >0$ và $\frac{1}{x^{2}}+\frac{1}{y^{2}}=\frac{1}{2}$. Tìm GTNN : $B=x^{2}y+x y^{2}$b) Cho $|x|+|y|+|z|=6$ Tìm GTNN : $C=|x-1|+|y-1|+|z-1|$
Đề bài: a) Cho $x,y >0$ và $\frac{1}{x^{2}}+\frac{1}{y^{2}}=\frac{1}{2}$. Tìm GTNN : $B=x^{2}y+x y^{2}$b) Cho $|x|+|y|+|z|=6$ Tìm GTNN : $C=|x-1|+|y-1|+|z-1|$ Lời giải Đáp số: $a) 16 b) 3$Thêm lời giải chi tiết … [Đọc thêm...] vềĐề: a) Cho $x,y >0$ và $\frac{1}{x^{2}}+\frac{1}{y^{2}}=\frac{1}{2}$. Tìm GTNN : $B=x^{2}y+x y^{2}$b) Cho $|x|+|y|+|z|=6$ Tìm GTNN : $C=|x-1|+|y-1|+|z-1|$
Đề: Cho ba số thực $x,y,z\geq 0$ thỏa mãn: $x^{1997}+y^{1997}+z^{1997}=3$.Tìm giá trị lớn nhất của biểu thức $F=x^2+y^2+z^2$
Đề bài: Cho ba số thực $x,y,z\geq 0$ thỏa mãn: $x^{1997}+y^{1997}+z^{1997}=3$.Tìm giá trị lớn nhất của biểu thức $F=x^2+y^2+z^2$ Lời giải Áp dụng bất đẳng thức Côsi cho $1995$ số $1$ và $2$ số $x^{1997}$, ta có: $\frac{1995+2x^{1997}}{1997}\geq \sqrt[1997]{x^{2.1997}}=x^2 (1)$Tương tự: $\frac{1995+2y^{1997}}{1997}\geq y^2 (2)$ … [Đọc thêm...] vềĐề: Cho ba số thực $x,y,z\geq 0$ thỏa mãn: $x^{1997}+y^{1997}+z^{1997}=3$.Tìm giá trị lớn nhất của biểu thức $F=x^2+y^2+z^2$
Đề: Cho hai đường thẳng \(d_1\) và \(d_2\) có phương trình: \(d_1: (a+b)x+y=1\) \(d_2: (a^2-b^2)x+ay=b\).a) Tìm giao điểm của \(d_1\) và \(d_2\) biện luận theo \(a,b\)b) Tìm điều kiện của \(a\) và \(b\) để \(d_1\) và \(d_2\) và trục hoành cắt nhau tại 1 điểm.
Đề bài: Cho hai đường thẳng \(d_1\) và \(d_2\) có phương trình: \(d_1: (a+b)x+y=1\) \(d_2: (a^2-b^2)x+ay=b\).a) Tìm giao điểm của \(d_1\) và \(d_2\) biện luận theo \(a,b\)b) Tìm điều kiện của \(a\) và \(b\) để \(d_1\) và \(d_2\) và trục hoành cắt nhau tại 1 điểm. Lời giải Giảia) Xét hệ phương trình: \(\begin{cases}(a-b)x+y=1 \\ … [Đọc thêm...] vềĐề: Cho hai đường thẳng \(d_1\) và \(d_2\) có phương trình: \(d_1: (a+b)x+y=1\) \(d_2: (a^2-b^2)x+ay=b\).a) Tìm giao điểm của \(d_1\) và \(d_2\) biện luận theo \(a,b\)b) Tìm điều kiện của \(a\) và \(b\) để \(d_1\) và \(d_2\) và trục hoành cắt nhau tại 1 điểm.
Đề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{4x+3}{x^{2}+1}$.
Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{4x+3}{x^{2}+1}$. Lời giải $y=\frac{4x+3}{x^{2}+1}=\frac{-\left ( x^{2}+1 \right )+\left ( x^{2}+4x+4 \right )}{x^{2}+1}=\frac{4\left ( x^{2}+1 \right )-\left (4x^{2}-4x+1 \right )}{x^{2}+1}$$=-1+\frac{\left ( x+2 \right )^{2}}{x^{2}+1}=4-\frac{\left ( 2x-1 \right )^{2}}{x^{2}+1}$Suy ra, giá trị nhỏ nhất … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{4x+3}{x^{2}+1}$.