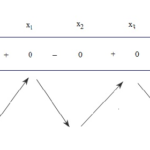
Đề bài: Tìm giá trị lớn nhất của biểu thức: $ R = x \cos y - y \cos x + (x-y) \left ( \frac{1}{2} xy - 1 \right ), (0 \leq x\leq y)$ Lời giải $Max R = 0 \left ( khi \left[ \begin{array}{l}x = y \ge 0\\x = 0 \le y\end{array} \right. \right ) $ … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất của biểu thức: $ R = x \cos y – y \cos x + (x-y) \left ( \frac{1}{2} xy – 1 \right ), (0 \leq x\leq y)$
Bài tập Hàm số
Đề: Tìm giá trị nhỏ nhất của biểu thức:$P = \cot ^4a + \cot ^4b + 2\tan ^2a.\tan ^2b + 2$
Đề bài: Tìm giá trị nhỏ nhất của biểu thức:$P = \cot ^4a + \cot ^4b + 2\tan ^2a.\tan ^2b + 2$ Lời giải $P=(cot^2a-cot^2b)^2+2(cotacotb-tanatanb)^2+6\geq 6$Với $a=b=\frac{\pi}{4} $ thì $P=6$. Vậy $min P=6$ … [Đọc thêm...] vềĐề: Tìm giá trị nhỏ nhất của biểu thức:$P = \cot ^4a + \cot ^4b + 2\tan ^2a.\tan ^2b + 2$
Đề: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x – 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau
Đề bài: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x - 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau Lời giải $1$. Bạn đọc tự giải$2$. Xét \(A\left( {0,a} \right)\) trên $Oy$. Đường thẳng qua $A$ với hệ số góc $k$ có phương trình \(y = kx + … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + 2x + 1}}{{x – 1}}\left( C \right)\)$1$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số$2$. Tìm tất cả các điểm trên trục tung sao cho từ đó có hai tiếp tuyến với đồ thị $(C)$ vuông góc với nhau
Đề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y=\frac{\cos x+2\sin x+3}{2\cos x-\sin x+4}$, với $-\pi
Đề bài: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y=\frac{\cos x+2\sin x+3}{2\cos x-\sin x+4}$, với $-\pi Lời giải Biến đổi hàm số về dạng: $(2y-1)\cos x-(y+2)\sin x=3-4y (1)$Phương trình $(1)$ có nghiệm khi: $(2y-1)^2+(y+2)^2\geq (3-4y)^2\Leftrightarrow 11y^2-24y+4\leq 0\Leftrightarrow \frac{2}{11}\leq y \leq 2$.Vậy, ta có: - … [Đọc thêm...] vềĐề: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số: $y=\frac{\cos x+2\sin x+3}{2\cos x-\sin x+4}$, với $-\pi
Đề: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị.
Đề bài: Cho hàm số \(y = - {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị. Lời giải $1$. Bạn đọc tự giải.$2$. Với \(m = 1\), có \(y = f\left( … [Đọc thêm...] vềĐề: Cho hàm số \(y = – {x^4} + 2m{x^2}\left( {{C_m}} \right)\)$1$. Khảo sát hàm số \(\left( {{C_m}} \right)\) với \(m = 1\)$2$. Viết phương trình tiếp tuyến của đồ thị hàm số vừa khảo sát tại điểm \(A\left( {\sqrt 2 ,\,0} \right)\)$3$. Hãy xác định m để hàm số \(\left( {{C_m}} \right)\) có ba cực trị.
Đề: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y – x + 6 = 0$
Đề bài: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y - x + 6 = 0$ Lời giải $1)$ Viết lại biểu … [Đọc thêm...] vềĐề: Xét hàm số $y = \frac{{{x^2} + 3x + 3}}{{x + 2}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên, từ đó suy ra đồ thị của hàm số$y = \left| {\frac{{{x^2} + 3x + 3}}{{x + 2}}} \right|$2) Viết phương trình tiếp tuyến với đường cong (1) biết rằng tiếp tuyến này vuông góc với đường thẳng $3y – x + 6 = 0$
Đề: Tìm $m$ để $Q=x^2+4y^2+my+3 \geq 0, \forall x \in R, \forall y\in R$
Đề bài: Tìm $m$ để $Q=x^2+4y^2+my+3 \geq 0, \forall x \in R, \forall y\in R$ Lời giải * Xem $Q$ là tam thức bậc hai đới với ẩn $x, \Delta'=-(4y^2+my+3)$Ta thấy $Q\geq 0, \forall x\in R, \forall y \in R \Leftrightarrow \Delta' \leq 0, \forall y\in R \Leftrightarrow 4y^2+my+3 \geq 0, \forall y \in R$Gọi $f(y)=4y^2+my+3, \delta=m^2-16.3$. Theo $(I) : … [Đọc thêm...] vềĐề: Tìm $m$ để $Q=x^2+4y^2+my+3 \geq 0, \forall x \in R, \forall y\in R$
Đề: Cho \(a>0,x,y\) là \(2\) số dương thỏa \(a(x+y)\sqrt{3}=xy\)Tìm giá trị nhỏ nhất của \(xy\) và của \(x^{2}+y^{2}-xy\).
Đề bài: Cho \(a>0,x,y\) là \(2\) số dương thỏa \(a(x+y)\sqrt{3}=xy\)Tìm giá trị nhỏ nhất của \(xy\) và của \(x^{2}+y^{2}-xy\). Lời giải Từ giả thiết: \(a(x+y)\sqrt{3}=xy \Rightarrow xy=a\sqrt{3}(x+y)\geq a\sqrt{3} 2\sqrt{xy}\)\(\Rightarrow xy\geq 12a^{2}\)Vậy \(xy\) nhỏ nhất là \(12a^{2}\) khi \(x=y=2a\sqrt{3}\) \(x^{2}+y^{2}-xy\geq 2xy-xy=xy\geq 12a^{2}\)\(\Rightarrow … [Đọc thêm...] vềĐề: Cho \(a>0,x,y\) là \(2\) số dương thỏa \(a(x+y)\sqrt{3}=xy\)Tìm giá trị nhỏ nhất của \(xy\) và của \(x^{2}+y^{2}-xy\).
Đề: Chứng minh rằng phương trình : $ (4x-3) \log_{2010}x + \frac{2x^2-3x+1}{x\ln 2010} = 0$ có nghiệm trên $\left ( \frac{1}{2} ;1 \right )$
Đề bài: Chứng minh rằng phương trình : $ (4x-3) \log_{2010}x + \frac{2x^2-3x+1}{x\ln 2010} = 0$ có nghiệm trên $\left ( \frac{1}{2} ;1 \right )$ Lời giải Cần giải chi tiết … [Đọc thêm...] vềĐề: Chứng minh rằng phương trình : $ (4x-3) \log_{2010}x + \frac{2x^2-3x+1}{x\ln 2010} = 0$ có nghiệm trên $\left ( \frac{1}{2} ;1 \right )$
Đề: Cho hàm số \(y = \frac{{{x^2} – x – 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} – \left( {1 + m} \right)|x| – m – 1 = 0\)
Đề bài: Cho hàm số \(y = \frac{{{x^2} - x - 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} - \left( {1 + m} \right)|x| - m - 1 = 0\) Lời … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} – x – 1}}{{x + 1}}\)$1$. Khảo sát hàm số đã cho$2$. Một đường thẳng thay đổi song song với đường thẳng \(y = \frac{1}{2}x\), cắt đồ thị của hàm số đã cho tại các điểm $M, N$. tìm quỹ tích trung điểm $I$ của $MN$.$3$. Biện luận theo tham số $m$ số nghiệm của phương trình sau \({x^2} – \left( {1 + m} \right)|x| – m – 1 = 0\)