Đề bài: Tính đạo hàm của các hàm số sau : $ y = \sqrt{x + \sqrt{x^2-x+1}}$ Lời giải Ta có : $ y' = (\sqrt{x+ \sqrt{x^2+x+1} })' = \frac{1}{2 \sqrt{x+\sqrt{x^2+x+1} } } (x+\sqrt{x^2-x+1})'$ $ = \frac{1}{2\sqrt{x+\sqrt{x^2-x+1} } }\left ( 1+\frac{2x-1}{2 \sqrt{x^2-x+1} } \right ) = \frac{2\sqrt{x^2-x+1}+2x-1 }{4\sqrt{x+\sqrt{x^2-x+1}}.\sqrt{x^2-x+1} }$ … [Đọc thêm...] vềĐề: Tính đạo hàm của các hàm số sau : $ y = \sqrt{x + \sqrt{x^2-x+1}}$
Bài tập Hàm số
Đề: Cho hàm số: $y = \frac{3(x + 1)}{x – 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên.
Đề bài: Cho hàm số: $y = \frac{3(x + 1)}{x - 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên. Lời giải $1.$ Bạn đọc tự giải$2.$ Phương trình tiếp tuyến tại điểm $M_0(x_0,y_0)\in (C)$ là$y=-\frac{9}{(x_0-2)^2}(x-x_0)+y_0 … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{3(x + 1)}{x – 2}\,\,\,\,(C)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số.$2$. Viết phương trình các đường thẳng đi qua $O(0;0)$ và tiếp xúc với $(C).$$3$. Tìm tất cả các điểm trên ($C$) có tọa độ là các số nguyên.
Đề: Cho parabol $y=x^2+x (P)$. Viết phương trình tiếp tuyến của $(P)$ tại điểm có hoành độ $x=2$
Đề bài: Cho parabol $y=x^2+x (P)$. Viết phương trình tiếp tuyến của $(P)$ tại điểm có hoành độ $x=2$ Lời giải Điểm $M$ có hoành độ $2$ thì tung độ là $2^2+2=6$$a_{tt}=y'(2)=5$. Tiếp tuyến tại $M(2;6)$ có phương trình là: $y-6=5(x-2)$ hay $y=5x-4$ … [Đọc thêm...] vềĐề: Cho parabol $y=x^2+x (P)$. Viết phương trình tiếp tuyến của $(P)$ tại điểm có hoành độ $x=2$
Đề: Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x + 1}}\)$1$. Xác định tất cả các giá trị của tham số $m$ để đồ thị của hàm số có các điểm cực đại, cực tiểu nằm về hai phía của trục tung.$2$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $m = 4$.
Đề bài: Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x + 1}}\)$1$. Xác định tất cả các giá trị của tham số $m$ để đồ thị của hàm số có các điểm cực đại, cực tiểu nằm về hai phía của trục tung.$2$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $m = 4$. Lời giải $1$. \(y' = \frac{{{x^2} + 2x + 1 - m}}{{{{\left( {x + 1} \right)}^2}}}\) Đồ thị có các điểm cực đại, cực … [Đọc thêm...] vềĐề: Cho hàm số \(y = \frac{{{x^2} + x + m}}{{x + 1}}\)$1$. Xác định tất cả các giá trị của tham số $m$ để đồ thị của hàm số có các điểm cực đại, cực tiểu nằm về hai phía của trục tung.$2$. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $m = 4$.
Đề: Cho hàm số $y=f(x)=x+\frac{2}{\sqrt{10-x}}$. Tính $f(2),f(6)$
Đề bài: Cho hàm số $y=f(x)=x+\frac{2}{\sqrt{10-x}}$. Tính $f(2),f(6)$ Lời giải $f\left ( 2 \right )=2+\frac{2}{\sqrt{10-2}}=2+\frac{\sqrt{2}}{2}$; $f\left ( 6 \right )=6+\frac{2}{\sqrt{10-6}}=7$ … [Đọc thêm...] vềĐề: Cho hàm số $y=f(x)=x+\frac{2}{\sqrt{10-x}}$. Tính $f(2),f(6)$
Đề: Cho hàm số: $y = \frac{mx^2 + 3mx + 2m + 1}{x + 2} (1)$1) Chứng minh rằng với mọi giá trị $m$, tiệm cận xiên (hay ngang) của đồ thị hàm số $(1)$ luôn đi qua một điểm cố định.2) Với mỗi giá trị $m$ cho trước, hãy viết phương trình đường thẳng đi qua điểm $A( – 1;0)$ và tiếp xúc với đồ thị hàm số $(1)$
Đề bài: Cho hàm số: $y = \frac{mx^2 + 3mx + 2m + 1}{x + 2} (1)$1) Chứng minh rằng với mọi giá trị $m$, tiệm cận xiên (hay ngang) của đồ thị hàm số $(1)$ luôn đi qua một điểm cố định.2) Với mỗi giá trị $m$ cho trước, hãy viết phương trình đường thẳng đi qua điểm $A( - 1;0)$ và tiếp xúc với đồ thị hàm số $(1)$ Lời giải $1)$ Trong trường hợp tổng quát ta biến … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{mx^2 + 3mx + 2m + 1}{x + 2} (1)$1) Chứng minh rằng với mọi giá trị $m$, tiệm cận xiên (hay ngang) của đồ thị hàm số $(1)$ luôn đi qua một điểm cố định.2) Với mỗi giá trị $m$ cho trước, hãy viết phương trình đường thẳng đi qua điểm $A( – 1;0)$ và tiếp xúc với đồ thị hàm số $(1)$
Đề: Chứng minh rằng: với $x > 0$ , ta luôn có: $e^x > 1 + x + \frac{x^2}{2}$
Đề bài: Chứng minh rằng: với $x > 0$ , ta luôn có: $e^x > 1 + x + \frac{x^2}{2}$ Lời giải Ta có: $f(x) = {e^x} - 1 - x - \frac{{{x^2}}}{2} \Rightarrow f'(x) = {e^x} - 1 - x \Rightarrow f''(x) = {e^x} - 1 > 0\forall x > 0$ $ \Rightarrow f'(x)$đồng biến với $x > 0 \Rightarrow f'(x) > f'(0) = 0\forall x > 0$ $ \Rightarrow f(x)$đồng biến với $x > 0 \Rightarrow f(x) > … [Đọc thêm...] vềĐề: Chứng minh rằng: với $x > 0$ , ta luôn có: $e^x > 1 + x + \frac{x^2}{2}$
Đề: Chứng minh rằng nếu các hàm số $ u = u(x), v = v(x)$ có đạo hàm tại điểm $x_0$ thì tại điểm đó ta có : $d(uv) = vdu + udv$
Đề bài: Chứng minh rằng nếu các hàm số $ u = u(x), v = v(x)$ có đạo hàm tại điểm $x_0$ thì tại điểm đó ta có : $d(uv) = vdu + udv$ Lời giải Ta có : $d(uv) = (uv)'_xdx=(u'_xv+uv'_x)dx = u'+xvdx + uv'_xdx$ $ = v(u'_xdx)+u(v'_xdx)=vdu+udv$. … [Đọc thêm...] vềĐề: Chứng minh rằng nếu các hàm số $ u = u(x), v = v(x)$ có đạo hàm tại điểm $x_0$ thì tại điểm đó ta có : $d(uv) = vdu + udv$
Đề: Dùng định nghĩa, tính đạo hàm của hàm số: $f(x) = x^2 + 4x$ tại điểm $x_0=2$.
Đề bài: Dùng định nghĩa, tính đạo hàm của hàm số: $f(x) = x^2 + 4x$ tại điểm $x_0=2$. Lời giải Ta có : $f'(2) = \mathop {\lim }\limits_{x \to 2}\frac{f(x)-f(2)}{x-2} = \mathop {\lim }\limits_{x \to 2}\frac{(x^2+4x)-12 }{x-2} = \mathop {\lim }\limits_{x \to 2}(x+6) = 8$. … [Đọc thêm...] vềĐề: Dùng định nghĩa, tính đạo hàm của hàm số: $f(x) = x^2 + 4x$ tại điểm $x_0=2$.
Đề: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$
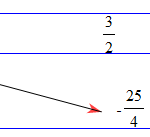
Đề bài: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$ Lời giải Giải* Tập xác định $R$* Sự biến thiên: Ta có: $a=1>0, -\frac{b}{2a}=\frac{3}{2}, -\frac{\Delta}{4a}=-\frac{25}{4}$. Vậy đồ thị hàm số $y=x^2-3x-4$ là parabol có đỉnh $I(\frac{3}{2};-\frac{25}{4})$, nhận đường thẳng $x=\frac{3}{2}$ làm tâm đối xứng và bề lõm hướng lên trên. Suy ra: Hàm số nghịch biến trên khoảng … [Đọc thêm...] vềĐề: Khảo sát và vẽ đồ thị hàm số $y=x^2-3x-4$