Đề bài: Xác định \(m\) để hàm số sau xác định trên \((-1,0)\): \(y=\frac{x+2m}{x-m+1}\) Lời giải \(y\) xác định \(\Leftrightarrow x-m+1\neq 0 \Leftrightarrow x\neq m-1\)Vậy để \(y\) xác định trên \((-1;0)\) thì m-1 phải ngoài khoảng đó để x luôn khác m-1.$\Leftrightarrow m-1\notin(-1;0)$$\Leftrightarrow \left[ \begin{array}{l} m-1\le-1\\ m-1\ge0 \end{array} … [Đọc thêm...] vềĐề: Xác định \(m\) để hàm số sau xác định trên \((-1,0)\): \(y=\frac{x+2m}{x-m+1}\)
Bài tập Hàm số
Đề: Cho các số thực $a, b, c $ thỏa $a+b+c=1$. Tìm giá trị nhỏ nhất của biểu thức $M=3 \left( a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2} \right) +3 \left( ab+bc+ca \right) + 2 \sqrt{ a^{2} + b^{2} + c^{2} }$
Đề bài: Cho các số thực $a, b, c $ thỏa $a+b+c=1$. Tìm giá trị nhỏ nhất của biểu thức $M=3 \left( a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2} \right) +3 \left( ab+bc+ca \right) + 2 \sqrt{ a^{2} + b^{2} + c^{2} }$ Lời giải Lưu ý: $ a^{2} + b^{2} + c^{2} = \left( a+b+c \right)^{2} – 2 \left( ab+bc+ca \right) = 1- 2 \left( ab+bc+ca \right) $$3 \left( a^{2} b^{2} + … [Đọc thêm...] vềĐề: Cho các số thực $a, b, c $ thỏa $a+b+c=1$. Tìm giá trị nhỏ nhất của biểu thức $M=3 \left( a^{2} b^{2} + b^{2} c^{2} + c^{2} a^{2} \right) +3 \left( ab+bc+ca \right) + 2 \sqrt{ a^{2} + b^{2} + c^{2} }$
Đề: Xét dấu hàm số: $f(x) = \sqrt{x+4} – \sqrt{1-x} – \sqrt{1-2x}$
Đề bài: Xét dấu hàm số: $f(x) = \sqrt{x+4} - \sqrt{1-x} - \sqrt{1-2x}$ Lời giải Hàm số $f(x)$ liên tục trên $[-4,\frac{1}{2} ]$.Giải phương trình $f(x) = 0$, ta có : $f(x) = 0 \Leftrightarrow \sqrt{1-x}+\sqrt{1-2x} = \sqrt{x+4}$ $\begin{cases}1-x > = 0\\ 1-2x \geq 0\\ 1-x+1-2x+2\sqrt{(1-x)(1-2x)}=x+4 \end{cases}\Leftrightarrow \begin{cases}x \leq 1 \\ x\leq … [Đọc thêm...] vềĐề: Xét dấu hàm số: $f(x) = \sqrt{x+4} – \sqrt{1-x} – \sqrt{1-2x}$
Đề: Cho $ m \in N.$ Tìm giá trị nhỏ nhất của: $f(x) = \int\limits_{1}^{x}t^m.e^{2t} -2 \left ( \frac{x^{m+3}}{m+3} +\frac{x^{m+2}}{m+2} \right ) , x\geq 1$
Đề bài: Cho $ m \in N.$ Tìm giá trị nhỏ nhất của: $f(x) = \int\limits_{1}^{x}t^m.e^{2t} -2 \left ( \frac{x^{m+3}}{m+3} +\frac{x^{m+2}}{m+2} \right ) , x\geq 1$ Lời giải Xét $ g(x) = e^{2x} - 2 (x^2 +x), x\geq 0$ $ g'(x) = 2e^{2x} - 2 (2x + 1) = 2 (e^{2x} -2x-1)$ $ g''(x) = 2 (2e^{2x} -2 ) = 4 (e^{2x}-1) \geq 0, \forall x \geq 0 $$\Rightarrow g' $ tăng trên … [Đọc thêm...] vềĐề: Cho $ m \in N.$ Tìm giá trị nhỏ nhất của: $f(x) = \int\limits_{1}^{x}t^m.e^{2t} -2 \left ( \frac{x^{m+3}}{m+3} +\frac{x^{m+2}}{m+2} \right ) , x\geq 1$
Đề: Tìm giá trị nhất của hàm số:$y=f(\alpha)=\sqrt{\cos ^{2} \alpha -2\cos \alpha +2}+\sqrt{\cos ^{2} \alpha +6\cos \alpha +13}$
Đề bài: Tìm giá trị nhất của hàm số:$y=f(\alpha)=\sqrt{\cos ^{2} \alpha -2\cos \alpha +2}+\sqrt{\cos ^{2} \alpha +6\cos \alpha +13}$ Lời giải Ta có: $y=f(\alpha)=\sqrt{(1-\cos \alpha) ^{2} +1}+\sqrt{(\cos \alpha+3)^{2} +4}$Trong mặt phẳng với hệ tọa độ Đề-các vuông góc,đặt:$\overrightarrow {u}=(1-\cos \alpha;1),\overrightarrow {v}=(\cos \alpha+3;2)$$\Rightarrow … [Đọc thêm...] vềĐề: Tìm giá trị nhất của hàm số:$y=f(\alpha)=\sqrt{\cos ^{2} \alpha -2\cos \alpha +2}+\sqrt{\cos ^{2} \alpha +6\cos \alpha +13}$
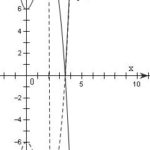
Đề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x^3 – 3x^2 – 6$$2.$ Khi $a$ thay đổi hãy biện luận số nghiệm của phương trình: $| x^3 – 3x^2- 6| = a$
Đề bài: $1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x^3 - 3x^2 - 6$$2.$ Khi $a$ thay đổi hãy biện luận số nghiệm của phương trình: $| x^3 - 3x^2- 6| = a$ Lời giải $1.$ Bạn đọc tự giải$2.$ Trước hết dựng đồ thị y = $\left| {{x^3} - 3{x^2} - 6} \right|$Suy ra từ đồ thị vừa vẽ:Đường thẳng $y = a$ (song song với $Ox$) cắt đồ thị tại bao nhiêu điểm thì … [Đọc thêm...] vềĐề: $1.$ Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = x^3 – 3x^2 – 6$$2.$ Khi $a$ thay đổi hãy biện luận số nghiệm của phương trình: $| x^3 – 3x^2- 6| = a$
Đề: Cho $a,b,c$ là các hằng số thỏa mãn $\frac{a}{2010}+\frac{b}{2009}+\frac{c}{2008} = 0$. Chứng minh phương trình $ax^2 + bx + c=0$ có nghiệm trên $(0;1).$
Đề bài: Cho $a,b,c$ là các hằng số thỏa mãn $\frac{a}{2010}+\frac{b}{2009}+\frac{c}{2008} = 0$. Chứng minh phương trình $ax^2 + bx + c=0$ có nghiệm trên $(0;1).$ Lời giải Xét $f(x) = ax^{2009} + bx^{2008}+cx^{2007}, x \in R$$\Rightarrow F(x) = \int\limits_{0}^{x} f(t)dt = \frac{ax^{2010}}{2010} + \frac{bx^{2009}}{2009}+\frac{cx^{2008}}{2008}$ khả vi trên $R$ và thỏa mãn … [Đọc thêm...] vềĐề: Cho $a,b,c$ là các hằng số thỏa mãn $\frac{a}{2010}+\frac{b}{2009}+\frac{c}{2008} = 0$. Chứng minh phương trình $ax^2 + bx + c=0$ có nghiệm trên $(0;1).$
Đề: Cho hàm số: $y = {x^3} – 3x\,\,(1)$$1$. Khảo sát hàm số ($1).$$2$. Chứng minh rằng khi $m$ thay đổi, đường thẳng cho bởi phương trình $y = m(x + 1) + 2$ luôn cắt đồ thị hàm số ($1$) tại một điểm $A$ cố định.Hãy xác định các giá trị của $m$ để đường thẳng cắt đồ thị hàm số ($1$) tại $3$ điểm $A, B, C$ khác nhau sao cho tiếp tuyến với đồ thị tại $B$ và $C$ vuông góc với nhau.
Đề bài: Cho hàm số: $y = {x^3} - 3x\,\,(1)$$1$. Khảo sát hàm số ($1).$$2$. Chứng minh rằng khi $m$ thay đổi, đường thẳng cho bởi phương trình $y = m(x + 1) + 2$ luôn cắt đồ thị hàm số ($1$) tại một điểm $A$ cố định.Hãy xác định các giá trị của $m$ để đường thẳng cắt đồ thị hàm số ($1$) tại $3$ điểm $A, B, C$ khác nhau sao cho tiếp tuyến với đồ thị tại $B$ và $C$ vuông góc với … [Đọc thêm...] vềĐề: Cho hàm số: $y = {x^3} – 3x\,\,(1)$$1$. Khảo sát hàm số ($1).$$2$. Chứng minh rằng khi $m$ thay đổi, đường thẳng cho bởi phương trình $y = m(x + 1) + 2$ luôn cắt đồ thị hàm số ($1$) tại một điểm $A$ cố định.Hãy xác định các giá trị của $m$ để đường thẳng cắt đồ thị hàm số ($1$) tại $3$ điểm $A, B, C$ khác nhau sao cho tiếp tuyến với đồ thị tại $B$ và $C$ vuông góc với nhau.
Đề: Tính đạo hàm của mỗi hàm số sau trên khoảng xác định của nóa) $y = (x^2 – x + 1) e^x$ b) $y = (\sin x + \cos x)e^{3x}$c) $y = \frac{e^x + e^{-x}}{e^x – e{-x}} $ d) $y = \sqrt{e^x } – 2008^x $
Đề bài: Tính đạo hàm của mỗi hàm số sau trên khoảng xác định của nóa) $y = (x^2 - x + 1) e^x$ b) $y = (\sin x + \cos x)e^{3x}$c) $y = \frac{e^x + e^{-x}}{e^x - e{-x}} $ d) $y = \sqrt{e^x } - 2008^x $ Lời giải a) $y' = (x^2 - x + 1)' e^x + (x^2 - x + 1)(e^x)'$$= (2x - 1)e^x + … [Đọc thêm...] vềĐề: Tính đạo hàm của mỗi hàm số sau trên khoảng xác định của nóa) $y = (x^2 – x + 1) e^x$ b) $y = (\sin x + \cos x)e^{3x}$c) $y = \frac{e^x + e^{-x}}{e^x – e{-x}} $ d) $y = \sqrt{e^x } – 2008^x $
Đề: Giải phương trình $f^{'}(x)=0$, biết rằng$f(x)=3\cos x+4\sin x+5x$
Đề bài: Giải phương trình $f^{'}(x)=0$, biết rằng$f(x)=3\cos x+4\sin x+5x$ Lời giải Ta có $f^{'}(x)=-3\sin x+4\cos x+5$$f^{'}(x)=0 \Leftrightarrow -3\sin x+4\cos x+5=0\Leftrightarrow 3\sin x-4\cos x=5$$\Leftrightarrow \frac{3}{5}\sin x-\frac{4}{5}\cos x=0 (1)$Đặt $\begin{cases}\cos \varphi=\frac{3}{5} \\ \sin \varphi= \frac{4}{5}\end{cases}$$(1)\Leftrightarrow \sin … [Đọc thêm...] vềĐề: Giải phương trình $f^{'}(x)=0$, biết rằng$f(x)=3\cos x+4\sin x+5x$