Trắc nghiệm Thể tích đa diện

Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB = 3a,{\rm{ }}AD = DC = a.\) Gọi \(I\) là trung điểm của \(AD\), biết hai mặt phẳng \(\left( {SBI} \right)\) và \(\left( {SCI} \right)\) cùng vuông góc với đáy và đường thẳng \(SC\) tạo với đáy một góc \({60^0}.\) Gọi \(M\) điểm trên đoạn\(AB\) sao cho \(AM = 2a\). Khoảng cách giữa \(MD\) và … [Đọc thêm...] vềCho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\), \(AB = 3a,{\rm{ }}AD = DC = a.\) Gọi \(I\) là trung điểm của \(AD\), biết hai mặt phẳng \(\left( {SBI} \right)\) và \(\left( {SCI} \right)\) cùng vuông góc với đáy và đường thẳng \(SC\) tạo với đáy một góc \({60^0}.\) Gọi \(M\) điểm trên đoạn\(AB\) sao cho \(AM = 2a\). Khoảng cách giữa \(MD\) và \(SC\) bằng

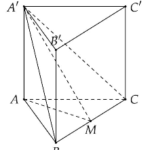
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác cân với \(AB = AC = a\), \(\widehat {BAC} = 120^\circ \). Mặt phẳng \((AB'C')\) tạo với đáy một góc \(60^\circ \) Tính thể tích \(V\) của khối lăng trụ đã cho. A. \(V = \frac{{3{a^3}}}{8}\). B. \(V = \frac{{9{a^3}}}{8}\). C. \(V = \frac{{{a^3}}}{8}\). D. \(V = \frac{{3{a^3}}}{4}\). Lời … [Đọc thêm...] vềCho khối lăng trụ đứng \(ABC.A’B’C’\) có đáy \(ABC\) là tam giác cân với \(AB = AC = a\), \(\widehat {BAC} = 120^\circ \). Mặt phẳng \((AB’C’)\) tạo với đáy một góc \(60^\circ \) Tính thể tích \(V\) của khối lăng trụ đã cho.

Cho khối lăng trụ \(ABC.A'B'C'\) có đáy là tam giác vuông cân tại \(B\) có \(AC = 3\sqrt 2 \). Hình chiếu vuông góc của \(A'\) trên mặt phẳng đáy là điểm \(H\) thuộc cạnh \(AC\) sao cho \(HC = 2HA\), biết góc giữa \(\left( {ABB'A'} \right)\) và mặt phẳng đáy bằng \(60^\circ \). Tính thể tích \(V\) của khối lăng trụ đã cho. A. \(V = 9\). B. \(V = \frac{9}{2}\). C. \(V … [Đọc thêm...] vềCho khối lăng trụ \(ABC.A’B’C’\) có đáy là tam giác vuông cân tại \(B\) có \(AC = 3\sqrt 2 \). Hình chiếu vuông góc của \(A’\) trên mặt phẳng đáy là điểm \(H\) thuộc cạnh \(AC\) sao cho \(HC = 2HA\), biết góc giữa \(\left( {ABB’A’} \right)\) và mặt phẳng đáy bằng \(60^\circ \). Tính thể tích \(V\) của khối lăng trụ đã cho.

Cho hình hộp chữ nhật\(ABCD.A'B'C'D'\). Khoảng cách giữa \(AB\) và \(B'C\) là \(\frac{{2a\sqrt 5 }}{5}\), giữa \(BC\) và \(AB'\) là \(\frac{{2a\sqrt 5 }}{5}\), giữa \(AC\) và \(BD'\) là \(\frac{{a\sqrt 3 }}{3}\). Thể tích của khối hộp đó là: A. \(2{a^3}\). B. \(4{a^3}\). C. \({a^3}\). D. \(8{a^3}\) Lời giải: Đặt \(AB = x\), \(AD = y\), \(AA' = z\). Gọi … [Đọc thêm...] vềCho hình hộp chữ nhật\(ABCD.A’B’C’D’\). Khoảng cách giữa \(AB\) và \(B’C\) là \(\frac{{2a\sqrt 5 }}{5}\), giữa \(BC\) và \(AB’\) là \(\frac{{2a\sqrt 5 }}{5}\), giữa \(AC\) và \(BD’\) là \(\frac{{a\sqrt 3 }}{3}\). Thể tích của khối hộp đó là:

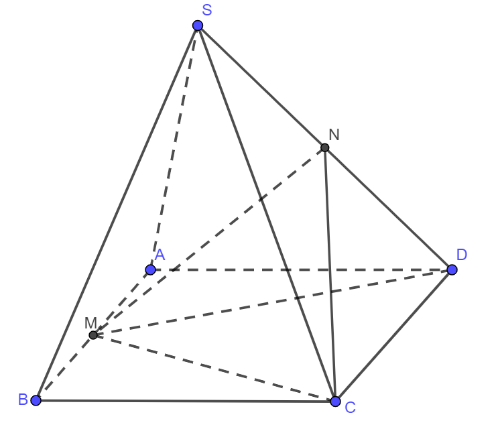
Cho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình chữ nhật. Gọi \(M,N\) lần lượt là trung điểm của \(AB,SD\). Tính tỉ số thể tích của hai khối chóp \(MNCD\) và \(S.ABCD\). A. \(\frac{{{V_{NMCD}}}}{{{V_{S.ABCD}}}} = \frac{1}{3}\). B. \(\frac{{{V_{NMCD}}}}{{{V_{S.ABCD}}}} = \frac{1}{8}\). C. \(\frac{{{V_{NMCD}}}}{{{V_{S.ABCD}}}} = \frac{1}{2}\). D. … [Đọc thêm...] vềCho hình chóp \(S.ABCD\)có đáy \(ABCD\) là hình chữ nhật. Gọi \(M,N\) lần lượt là trung điểm của \(AB,SD\). Tính tỉ số thể tích của hai khối chóp \(MNCD\) và \(S.ABCD\).

Cho khối lăng trụ \(ABC.A'B'C'\) có đáy là tam giác đều cạnh \(2\). Hình chiếu vuông góc của \(B'\) trên mặt phẳng đáy trùng trung điểm \(H\) của cạnh \(AB\), biết góc giữa \(B'H\) và mặt phẳng \(\left( {BCC'B'} \right)\) bằng \(45^\circ \). Tính thể tích \(V\) của khối lăng trụ đã cho. A. \(V = 3\). B. \(V = \frac{3}{2}\). C. \(V = \frac{{\sqrt 3 }}{2}\). D. \(V = … [Đọc thêm...] vềCho khối lăng trụ \(ABC.A’B’C’\) có đáy là tam giác đều cạnh \(2\). Hình chiếu vuông góc của \(B’\) trên mặt phẳng đáy trùng trung điểm \(H\) của cạnh \(AB\), biết góc giữa \(B’H\) và mặt phẳng \(\left( {BCC’B’} \right)\) bằng \(45^\circ \). Tính thể tích \(V\) của khối lăng trụ đã cho.

Cho khối lăng trụ \(ABC.A'B'C'\), khoảng cách từ \(C\) đến \(BB'\) là \(\sqrt 5 \), khoảng cách từ \(A\) đến \(BB'\) và \(CC'\) lần lượt là \(1;\,\,2\). Hình chiếu vuông góc của \(A\) lên mặt phẳng\(A'B'C'\) là trung điểm \(M\) của \(B'C'\), \(A'M = \frac{{\sqrt {15} }}{3}\). Thể tích của khối lăng trụ đã cho bằng A. \(\frac{{\sqrt {15} }}{3}\). B. \(\frac{{2\sqrt 5 … [Đọc thêm...] vềCho khối lăng trụ \(ABC.A’B’C’\), khoảng cách từ \(C\) đến \(BB’\) là \(\sqrt 5 \), khoảng cách từ \(A\) đến \(BB’\) và \(CC’\) lần lượt là \(1;\,\,2\). Hình chiếu vuông góc của \(A\) lên mặt phẳng\(A’B’C’\) là trung điểm \(M\) của \(B’C’\), \(A’M = \frac{{\sqrt {15} }}{3}\). Thể tích của khối lăng trụ đã cho bằng