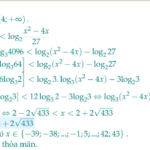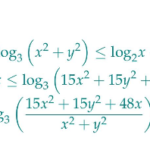Cho \(a,b\) là hai số thực dương, khác 1 và thỏa mãn \(\log _a^2\left( {ab} \right) = 4{\log _b}\frac{{{a^2}}}{b}\). Giá trị của \({\log _a}b\) bằng A. \( - 1\). B. \(1\). C. \(3\). D. \( - 3\). Lời giải: +) Đặt \(t = {\log _a}b\), do \(a,b\) là hai số thực dương, khác 1 nên \(t \ne 0\). +) Ta có \(\log _a^2\left( {ab} \right) = 4{\log … [Đọc thêm...] vềCho \(a,b\) là hai số thực dương, khác 1 và thỏa mãn \(\log _a^2\left( {ab} \right) = 4{\log _b}\frac{{{a^2}}}{b}\). Giá trị của \({\log _a}b\) bằng
Trắc nghiệm Logarit và hàm số lôgarit
Cho các số thực \(a,b\) thuộc khoảng \(\left( {0;1} \right)\) thoả mãn \({\log _{ab}}a = \log _a^2\left( {\frac{a}{b}} \right)\). Giá trị của biểu thức \(\frac{{\ln a}}{{\ln b}}\) bằng.
Cho các số thực \(a,b\) thuộc khoảng \(\left( {0;1} \right)\) thoả mãn \({\log _{ab}}a = \log _a^2\left( {\frac{a}{b}} \right)\). Giá trị của biểu thức \(\frac{{\ln a}}{{\ln b}}\) bằng. A. \(\sqrt 5 - 1\). B. \(\frac{{\sqrt 5 - 1}}{2}\). C. \(\frac{{1 + \sqrt 5 }}{2}\). D. \(\frac{{ - 1 - \sqrt 5 }}{2}\). Lời giải: Giả thiết: … [Đọc thêm...] vềCho các số thực \(a,b\) thuộc khoảng \(\left( {0;1} \right)\) thoả mãn \({\log _{ab}}a = \log _a^2\left( {\frac{a}{b}} \right)\). Giá trị của biểu thức \(\frac{{\ln a}}{{\ln b}}\) bằng.
Gọi \(S\) là tập các số nguyên \(x\) sao cho tồn tại số thực \(y\) thỏa mãn \({2^{x + y + 1}} = {\left( {\sqrt 3 } \right)^{{x^2} + {y^2}}}\). Tính tổng các phần tử của tập \(S\)?
Gọi \(S\) là tập các số nguyên \(x\) sao cho tồn tại số thực \(y\) thỏa mãn \({2^{x + y + 1}} = {\left( {\sqrt 3 } \right)^{{x^2} + {y^2}}}\). Tính tổng các phần tử của tập \(S\)? A. \(5\). B. \(6\). C. \(3\). D. \(2\). Lời giải: \({2^{x + y + 1}} = {\left( {\sqrt 3 } \right)^{{x^2} + {y^2}}} \Leftrightarrow {4^{x + y + 1}} = {3^{{x^2} + … [Đọc thêm...] vềGọi \(S\) là tập các số nguyên \(x\) sao cho tồn tại số thực \(y\) thỏa mãn \({2^{x + y + 1}} = {\left( {\sqrt 3 } \right)^{{x^2} + {y^2}}}\). Tính tổng các phần tử của tập \(S\)?
Cho \(a,\,b\)là các số thực thỏa mãn \(1 < a \le b \le {a^6}\).Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = {\left[ {{{\log }_a}\left( {\frac{{{a^2}}}{b}} \right)} \right]^2} + 3{\log _{\sqrt[4]{a}}}b – 1\) . Tính \(M + 2m\)?
Cho \(a,\,b\)là các số thực thỏa mãn \(1 < a \le b \le {a^6}\).Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = {\left[ {{{\log }_a}\left( {\frac{{{a^2}}}{b}} \right)} \right]^2} + 3{\log _{\sqrt[4]{a}}}b - 1\) . Tính \(M + 2m\)? A. \(12\). B. \(99\). C. \(87\). D. \(111\). Lời giải: Vì \(1 < a … [Đọc thêm...] về Cho \(a,\,b\)là các số thực thỏa mãn \(1 < a \le b \le {a^6}\).Gọi \(M,\,m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P = {\left[ {{{\log }_a}\left( {\frac{{{a^2}}}{b}} \right)} \right]^2} + 3{\log _{\sqrt[4]{a}}}b – 1\) . Tính \(M + 2m\)?
Số giá trị nguyên của tham số \(m\) để hàm số \(f\left( x \right) = {\left( {\log _2^2\left( {2x} \right) – 2m{{\log }_2}\left( {\frac{x}{2}} \right)} \right)^{\frac{1}{3}}}\) xác định với mọi \(x\) dương.
Số giá trị nguyên của tham số \(m\) để hàm số \(f\left( x \right) = {\left( {\log _2^2\left( {2x} \right) - 2m{{\log }_2}\left( {\frac{x}{2}} \right)} \right)^{\frac{1}{3}}}\) xác định với mọi \(x\) dương. A. \(3\). B. \(4\). C. \(5\). D. \(2\). Lời giải: Điều kiện xác định \(\left\{ {\begin{array}{*{20}{c}}{x > 0}\\{\log _2^2\left( … [Đọc thêm...] vềSố giá trị nguyên của tham số \(m\) để hàm số \(f\left( x \right) = {\left( {\log _2^2\left( {2x} \right) – 2m{{\log }_2}\left( {\frac{x}{2}} \right)} \right)^{\frac{1}{3}}}\) xác định với mọi \(x\) dương.
Có bao nhiêu số nguyên $x$ thỏa mãn $\log_{3} \frac{\left(x^{2}-4 x\right)^{2}}{4096}<\log_{2} \frac{x^{2}-4 x}{27}$ ?
Có bao nhiêu số nguyên $x$ thỏa mãn $\log_{3} \frac{\left(x^{2}-4 x\right)^{2}}{4096} … [Đọc thêm...] vềCó bao nhiêu số nguyên $x$ thỏa mãn $\log_{3} \frac{\left(x^{2}-4 x\right)^{2}}{4096}<\log_{2} \frac{x^{2}-4 x}{27}$ ?
Có bao nhiêu cặp số nguyên $(x ; y)$ thỏa mãn \(\log {2}\left(x^{2}+y^{2}+4 x\right)+\log {3}\left(x^{2}+y^{2}\right) \leq \log {2} x+\log {3}\left(15 x^{2}+15 y^{2}+48 x\right) ?\)
Câu 44: Có bao nhiêu cặp số nguyên $(x ; y)$ thỏa mãn $$\log _{2}\left(x^{2}+y^{2}+4 x\right)+\log _{3}\left(x^{2}+y^{2}\right) \leq \log _{2} x+\log _{3}\left(15 x^{2}+15 y^{2}+48 x\right) ?$$A. 22.B. 28 .C. 15 .D. 12 . … [Đọc thêm...] vềCó bao nhiêu cặp số nguyên $(x ; y)$ thỏa mãn \(\log {2}\left(x^{2}+y^{2}+4 x\right)+\log {3}\left(x^{2}+y^{2}\right) \leq \log {2} x+\log {3}\left(15 x^{2}+15 y^{2}+48 x\right) ?\)
Có bao nhiêu cặp số nguyên (x;y) thỏa mãn \({\log _3}\left( {{x^2} + {y^2} + x} \right) + {\log _2}\left( {{x^2} + {y^2}} \right) \le {\log _3}x + {\log _2}\left( {{x^2} + {y^2} + 24x} \right)?\)
Có bao nhiêu cặp số nguyên \((x;y)\) thỏa mãn \({\log _3}\left( {{x^2} + {y^2} + x} \right) + {\log _2}\left( {{x^2} + {y^2}} \right) \le {\log _3}x + {\log _2}\left( {{x^2} + {y^2} + 24x} \right)?\) A. 89. B. 48. C. 90. D. 49. Lời giải: Chọn B Điều kiện: \(x > 0\) . Ta có: \({\log … [Đọc thêm...] vềCó bao nhiêu cặp số nguyên (x;y) thỏa mãn \({\log _3}\left( {{x^2} + {y^2} + x} \right) + {\log _2}\left( {{x^2} + {y^2}} \right) \le {\log _3}x + {\log _2}\left( {{x^2} + {y^2} + 24x} \right)?\)
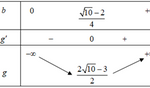
Cho các số thực dương \(a\), \(b\) thỏa mãn \(\ln \frac{{2 – 2ab}}{{a + b}} = 2ab + a + b – 2\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = a + 2b\).
Cho các số thực dương \(a\), \(b\) thỏa mãn \(\ln \frac{{2 - 2ab}}{{a + b}} = 2ab + a + b - 2\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = a + 2b\). A. \({P_{\min }} = \frac{{2\sqrt {10} - 3}}{2}\). B. \({P_{\min }} = \frac{{3\sqrt {10} - 7}}{2}\). C. \({P_{\min }} = \frac{{2\sqrt {10} - 1}}{2}\). D. \({P_{\min }} = \frac{{2\sqrt {10} - 5}}{2}\). Lời giải Điều … [Đọc thêm...] vềCho các số thực dương \(a\), \(b\) thỏa mãn \(\ln \frac{{2 – 2ab}}{{a + b}} = 2ab + a + b – 2\). Tìm giá trị nhỏ nhất \({P_{\min }}\) của \(P = a + 2b\).
\({2^{2{x^2} – 15x + 100}} – {2^{{x^2} + 10x – 50}} + {x^2} – 25x + 150 < 0\) là
\({2^{2{x^2} - 15x + 100}} - {2^{{x^2} + 10x - 50}} + {x^2} - 25x + 150 < 0\) là A. \(4\). B. \(6.\) C. \(3\). D. \(5\). Lời giải Ta có \({2^{2{x^2} - 15x + 100}} - {2^{{x^2} + 10x - 50}} + {x^2} - 25x + 150 < 0\) \( \Leftrightarrow {2^{2{x^2} - 15x + 100}} - {2^{{x^2} + 10x - 50}} + 2{x^2} - 15x + 100 - \left( {{x^2} + 10x - 50} \right) < … [Đọc thêm...] về\({2^{2{x^2} – 15x + 100}} – {2^{{x^2} + 10x – 50}} + {x^2} – 25x + 150 < 0\) là