Câu hỏi:
(Sở Thái Nguyên 2022) Cho hàm số đa thức bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau
Số điểm cực trị của hàm số \(g\left( x \right) = \left( {{x^3} - x} \right){\left[ {f\left( {x + 1} \right)} \right]^2}\) là
A. 11.
B. 8.
C. 13.
D. 10.
Lời giải:
Chọn D
Từ bảng biến thiên ta thấy rằng \(f(x) = 0\) có 4 nghiệm phân … [Đọc thêm...] về (Sở Thái Nguyên 2022) Cho hàm số đa thức bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau Số điểm cực trị của hàm số \(g\left( x \right) = \left( {{x^3} – x} \right){\left[ {f\left( {x + 1} \right)} \right]^2}\) là
Kết quả tìm kiếm cho: ty so
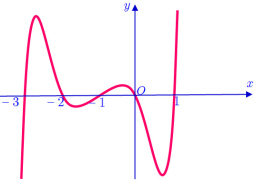
(Đại học Hồng Đức 2022) Cho hàm đa thức \(y = \left[ {f\left( {{x^2} + 2x} \right)} \right]\prime \) có đồ thị cắt trục \(Ox\) tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số \(m\) với \(2022m \in \mathbb{Z}\) để hàm số \(g(x) = f\left( {{x^2} – 2|x – 1| – 2x + m} \right)\) có 9 điểm cực trị?
Câu hỏi:
(Đại học Hồng Đức 2022) Cho hàm đa thức \(y = \left[ {f\left( {{x^2} + 2x} \right)} \right]\prime \) có đồ thị cắt trục \(Ox\) tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số \(m\) với \(2022m \in \mathbb{Z}\) để hàm số \(g(x) = f\left( {{x^2} - 2|x - 1| - 2x + m} \right)\) có 9 điểm cực trị?
A. 2020.
B. … [Đọc thêm...] về (Đại học Hồng Đức 2022) Cho hàm đa thức \(y = \left[ {f\left( {{x^2} + 2x} \right)} \right]\prime \) có đồ thị cắt trục \(Ox\) tại 5 điểm phân biệt như hình vẽ. Hỏi có bao nhiêu giá trị của tham số \(m\) với \(2022m \in \mathbb{Z}\) để hàm số \(g(x) = f\left( {{x^2} – 2|x – 1| – 2x + m} \right)\) có 9 điểm cực trị?
(Sở Hà Tĩnh 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ..
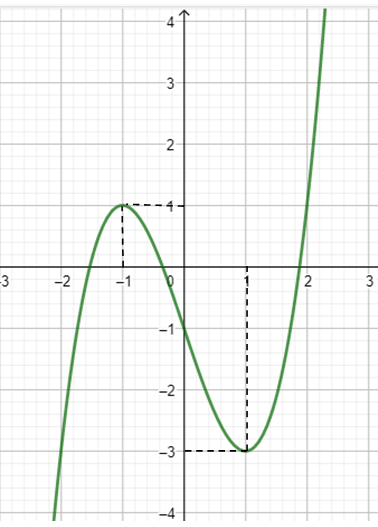
Tính tổng tất cả các giá trị nguyên của \(m\) để phương trình \(f\left( {1 – 2\sin x} \right) = m\) có đúng hai nghiệm trên \(\left[ {0;\pi } \right]\)
Câu hỏi:
(Sở Hà Tĩnh 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ..
Tính tổng tất cả các giá trị nguyên của \(m\) để phương trình \(f\left( {1 - 2\sin x} \right) = m\) có đúng hai nghiệm trên \(\left[ {0;\pi } \right]\)
A. \( - 3\).
B. \( - 2\).
C. \(0\).
D. \( - 6\).
Lời giải:
Chọn D
Xét phương … [Đọc thêm...] về (Sở Hà Tĩnh 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ.. Tính tổng tất cả các giá trị nguyên của \(m\) để phương trình \(f\left( {1 – 2\sin x} \right) = m\) có đúng hai nghiệm trên \(\left[ {0;\pi } \right]\)
(THPT Lương Thế Vinh – Hà Nội – 2022) Cho hàm số \(f(x)\) có đổ thị như hình vẽ:
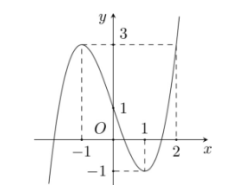
Gọi S là tập hợp tất cả các giá trị nguyên của tham số \(m\) để phương trình \(f\left( {3 – \sqrt {4 – {x^2}} } \right) = m\) có hai nghiệm phân biệt thuộc đoạn \([ – \sqrt 3 ;\sqrt 3 ]\). Số phần tử của \(S\) là
Câu hỏi:
(THPT Lương Thế Vinh – Hà Nội – 2022) Cho hàm số \(f(x)\) có đổ thị như hình vẽ:
Gọi S là tập hợp tất cả các giá trị nguyên của tham số \(m\) để phương trình \(f\left( {3 - \sqrt {4 - {x^2}} } \right) = m\) có hai nghiệm phân biệt thuộc đoạn \([ - \sqrt 3 ;\sqrt 3 ]\). Số phần tử của \(S\) là
A. \(1.\)
B. \(4.\)
C. \(5.\)
D. \(3.\)
Lời … [Đọc thêm...] về (THPT Lương Thế Vinh – Hà Nội – 2022) Cho hàm số \(f(x)\) có đổ thị như hình vẽ: Gọi S là tập hợp tất cả các giá trị nguyên của tham số \(m\) để phương trình \(f\left( {3 – \sqrt {4 – {x^2}} } \right) = m\) có hai nghiệm phân biệt thuộc đoạn \([ – \sqrt 3 ;\sqrt 3 ]\). Số phần tử của \(S\) là
(THPT Lê Thánh Tông – HCM-2022) Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị \(\left( {{C_1}} \right)\) và \(y = f’\left( x \right)\) có đồ thị \(\left( {{C_2}} \right)\) như hình vẽ dưới.
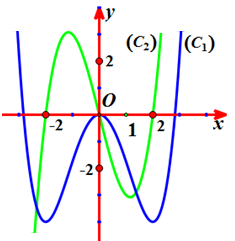
Số điểm cực đại của đồ thị hàm số \(g\left( x \right) = f\left[ {{e^{ – x}}f\left( x \right)} \right]\) trên khoảng \(\left( { – \infty \,;\,3} \right)\) là
Câu hỏi:
(THPT Lê Thánh Tông - HCM-2022) Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị \(\left( {{C_1}} \right)\) và \(y = f'\left( x \right)\) có đồ thị \(\left( {{C_2}} \right)\) như hình vẽ dưới.
Số điểm cực đại của đồ thị hàm số \(g\left( x \right) = f\left[ {{e^{ - x}}f\left( x \right)} \right]\) trên khoảng \(\left( { - \infty \,;\,3} \right)\) … [Đọc thêm...] về (THPT Lê Thánh Tông – HCM-2022) Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị \(\left( {{C_1}} \right)\) và \(y = f’\left( x \right)\) có đồ thị \(\left( {{C_2}} \right)\) như hình vẽ dưới. Số điểm cực đại của đồ thị hàm số \(g\left( x \right) = f\left[ {{e^{ – x}}f\left( x \right)} \right]\) trên khoảng \(\left( { – \infty \,;\,3} \right)\) là
\(\) (THPT Yên Lạc – Vĩnh Phúc – 2022) Cho hàm số \(f\left( x \right)\), đồ thị của hàm số \(y = f’\left( x \right)\) là đường cong trong hình bên.

Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(f\left( {2x} \right) + \frac{{8{x^3}}}{3} – 4x – m < 0\) đúng với mọi \(x \in \left[ { – \frac{1}{2};\frac{1}{2}} \right]\)
Câu hỏi:
\(\) (THPT Yên Lạc - Vĩnh Phúc - 2022) Cho hàm số \(f\left( x \right)\), đồ thị của hàm số \(y = f'\left( x \right)\) là đường cong trong hình bên.
Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(f\left( {2x} \right) + \frac{{8{x^3}}}{3} - 4x - m < 0\) đúng với mọi \(x \in \left[ { - \frac{1}{2};\frac{1}{2}} \right]\)
A. \(m > … [Đọc thêm...] về \(\) (THPT Yên Lạc – Vĩnh Phúc – 2022) Cho hàm số \(f\left( x \right)\), đồ thị của hàm số \(y = f’\left( x \right)\) là đường cong trong hình bên. Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(f\left( {2x} \right) + \frac{{8{x^3}}}{3} – 4x – m < 0\) đúng với mọi \(x \in \left[ { – \frac{1}{2};\frac{1}{2}} \right]\)
(Sở Ninh Bình 2022) Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như sau

Tìm \(m\) để phương trình \(|f(x – 1) + 2| = m\) có 4 nghiệm thỏa mãn \({x_1} < {x_2} < {x_3} < 1 < {x_4}\).
Câu hỏi:
(Sở Ninh Bình 2022) Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như sau
Tìm \(m\) để phương trình \(|f(x - 1) + 2| = m\) có 4 nghiệm thỏa mãn \({x_1} < {x_2} < {x_3} < 1 < {x_4}\).
A. \(4 < m < 6\).
B. \(3 < m < 6\).
C. \(2 < m < 6\).
D. \(2 < m < 4\).
Lời giải:.
Đồ thị hàm số … [Đọc thêm...] về (Sở Ninh Bình 2022) Cho hàm số \(y = f(x) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như sau Tìm \(m\) để phương trình \(|f(x – 1) + 2| = m\) có 4 nghiệm thỏa mãn \({x_1} < {x_2} < {x_3} < 1 < {x_4}\).
(THPT Hồ Nghinh – Quảng Nam – 2022) Cho hàm số \(y = f(x)\) có bảng biến thiên như sau

Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(6f\left( {{x^2} – 4x} \right) = m\) có it nhất 3 nghiệm
thực phân biệt thuộc khoảng \((0; + \infty )\) ?
Câu hỏi:
(THPT Hồ Nghinh – Quảng Nam – 2022) Cho hàm số \(y = f(x)\) có bảng biến thiên như sau
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(6f\left( {{x^2} - 4x} \right) = m\) có it nhất 3 nghiệm
thực phân biệt thuộc khoảng \((0; + \infty )\) ?
A. 29.
B. 25.
C. 24.
D. 30.
Lời giải:
Chọn D
Ta có: \(6f\left( {{x^2} - 4x} … [Đọc thêm...] về (THPT Hồ Nghinh – Quảng Nam – 2022) Cho hàm số \(y = f(x)\) có bảng biến thiên như sau Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(6f\left( {{x^2} – 4x} \right) = m\) có it nhất 3 nghiệm thực phân biệt thuộc khoảng \((0; + \infty )\) ?
Cho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( – \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = – 55\) .

Câu hỏi:
Cho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( - \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = - 55\) .
Diện tích miền tô đậm gần số nào nhất trong các số sau đây?
Lời Giải:
Đây là các câu … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) với đồ thị là Parabol đỉnh \(I\) có tung độ bằng \( – \frac{7}{{12}}\) và hàm số bậc ba \(g\left( x \right)\). Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ \({x_1},{x_2},{x_3}\) thoả mãn \(18{x_1}{x_2}{x_3} = – 55\) .
96. Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( x \right) < 0,\,\forall x > 0\) và có đạo hàm \(f’\left( x \right)\) liên tục trên khoảng \(\left( {0\,;\, + \infty } \right)\) thỏa mãn \(f’\left( x \right) = \left( {2x + 1} \right){f^2}\left( x \right),\,\forall x > 0\) và \(f\left( 1 \right) = – \frac{1}{2}\). Giá trị của biểu thức \(f\left( 1 \right) + f\left( 2 \right) + … + f\left( {2020} \right)\) bằng
Câu hỏi: 96. Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( x \right) < 0,\,\forall x > 0\) và có đạo hàm \(f'\left( x \right)\) liên tục trên khoảng \(\left( {0\,;\, + \infty } \right)\) thỏa mãn \(f'\left( x \right) = \left( {2x + 1} \right){f^2}\left( x \right),\,\forall x > 0\) và \(f\left( 1 \right) = - \frac{1}{2}\). Giá trị của biểu thức … [Đọc thêm...] về96. Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( x \right) < 0,\,\forall x > 0\) và có đạo hàm \(f’\left( x \right)\) liên tục trên khoảng \(\left( {0\,;\, + \infty } \right)\) thỏa mãn \(f’\left( x \right) = \left( {2x + 1} \right){f^2}\left( x \right),\,\forall x > 0\) và \(f\left( 1 \right) = – \frac{1}{2}\). Giá trị của biểu thức \(f\left( 1 \right) + f\left( 2 \right) + … + f\left( {2020} \right)\) bằng
