[Mức độ 4] Tìm tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = \frac{{x - \sqrt {{x^2} + 3} }}{{\sqrt {m{x^2} + 1} }}\) có tiệm cận ngang. A. \(m \le 0\) B. \(m = 1\) hoặc \(m = 4\). C. \(m \ge 0\) D. \(m > 0\). Lời giải: Điều kiện: \(m{x^2} + 1 > 0\) + TH1: \(m = 0\). Ta có: \(y = \left( {x - \sqrt {{x^2} + 3} } \right)\) \(\mathop … [Đọc thêm...] về[Mức độ 4] Tìm tất cả các giá trị của tham số \(m\) để đồ thị hàm số \(y = \frac{{x – \sqrt {{x^2} + 3} }}{{\sqrt {m{x^2} + 1} }}\) có tiệm cận ngang.
Kết quả tìm kiếm cho: ty so
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 2x\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( { – 2;4} \right)\)?
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = {x^2} - 2x\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} - 3{x^2} + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( { - 2;4} \right)\)? A. \(3\). B. \(4\). C. \(5\). D. … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f’\left( x \right) = {x^2} – 2x\) với mọi \(x \in \mathbb{R}\). Có bao nhiêu giá trị nguyên của tham số \(m\) sao cho ứng với mỗi \(m\), hàm số \(g\left( x \right) = f\left( {{x^3} – 3{x^2} + m} \right)\) có đúng ba điểm cực trị thuộc khoảng \(\left( { – 2;4} \right)\)?
[Mức độ 4] Xét các số thực dương \(x,\,\,y\) thỏa mãn \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} – {x^2}{y^2} – 2{y^2}x\). Khi biểu thức \(4y – {x^2}\) đạt giá trị lớn nhất thì giá trị của biểu thức \(3x + 2y\) bằng
[Mức độ 4] Xét các số thực dương \(x,\,\,y\) thỏa mãn \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} - {x^2}{y^2} - 2{y^2}x\). Khi biểu thức \(4y - {x^2}\) đạt giá trị lớn nhất thì giá trị của biểu thức \(3x + 2y\) bằng A. \(\frac{{11}}{2}\). B. \(\frac{7}{2}\). C.\(3\). D. \(4\). Lời giải: *) Ta có: \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} - … [Đọc thêm...] về[Mức độ 4] Xét các số thực dương \(x,\,\,y\) thỏa mãn \(\log \frac{{x + 1}}{{2y + 1}} = 4{y^4} + 4{y^3} – {x^2}{y^2} – 2{y^2}x\). Khi biểu thức \(4y – {x^2}\) đạt giá trị lớn nhất thì giá trị của biểu thức \(3x + 2y\) bằng
[Mức độ 4] Cho hai hàm số \(y = {x^6} + 6{x^4} + 6{x^2} + 1\) và \(y = {x^3}\sqrt {m – 15x} \left( {m + 3 – 15x} \right)\) có đồ thị lần lượt là \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\). Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 2024;2024} \right]\) để \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp \(S\) bằng
[Mức độ 4] Cho hai hàm số \(y = {x^6} + 6{x^4} + 6{x^2} + 1\) và \(y = {x^3}\sqrt {m - 15x} \left( {m + 3 - 15x} \right)\) có đồ thị lần lượt là \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\). Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2024;2024} \right]\) để \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) cắt … [Đọc thêm...] về[Mức độ 4] Cho hai hàm số \(y = {x^6} + 6{x^4} + 6{x^2} + 1\) và \(y = {x^3}\sqrt {m – 15x} \left( {m + 3 – 15x} \right)\) có đồ thị lần lượt là \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\). Gọi \(S\) là tập hợp tất cả các giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { – 2024;2024} \right]\) để \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) cắt nhau tại hai điểm phân biệt. Số phần tử của tập hợp \(S\) bằng
[ Mức độ 3] Cho Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(2f\left( {2{x^3} – 6x + 1} \right) + 3 = m\) có \(7\)nghiệm phân biệt.

[ Mức độ 3] Cho Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(2f\left( {2{x^3} - 6x + 1} \right) + 3 = m\) có \(7\)nghiệm phân biệt. A. \(6\). B. \(7\). C. \(8\). D. \(9\) Lời giải: Đặt \(t = 2{x^3} - 6x + 1\) . \( \Rightarrow t' = 6{x^2} - 6 = 0 \Leftrightarrow x = \pm … [Đọc thêm...] về[ Mức độ 3] Cho Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hỏi có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(2f\left( {2{x^3} – 6x + 1} \right) + 3 = m\) có \(7\)nghiệm phân biệt.
Cho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\)
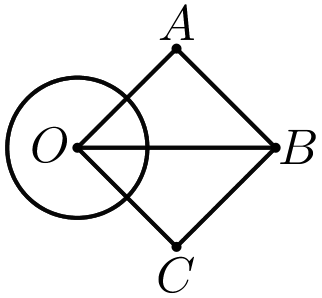
Cho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\) A. \(V = \frac{{8\left( {3 + 4\sqrt 2 } \right)\pi }}{3}.\) B. \(V = \frac{{8\left( {2 + 5\sqrt 2 } \right)\pi }}{3}.\) C. \(V = \frac{{8\left( {3 + … [Đọc thêm...] vềCho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\)
Để tính thể tích lọ gốm, người ta xấp xỉ nó bởi khối tròn xoay sinh bởi phần hình phẳng (phần gạch ngang) giới hạn bởi hai hàm bậc hai \(y = f\left( x \right)\) và \(y = g\left( x \right)\)như hình vẽ. Biết tọa độ đỉnh của hai parabol là \(I\left( {0\,;\, – 7} \right)\), điểm \(A\left( { – 7\,;\, – 4,06} \right)\) thuộc đồ thị \(y = g\left( x \right)\) và điểm \(B\left( {15\,;\, – 2,5} \right)\) thuộc đồ thị \(y = f\left( x \right)\). Tính thể tích xấp xỉ của lọ gốm (làm tròn đến hàng đơn vị).

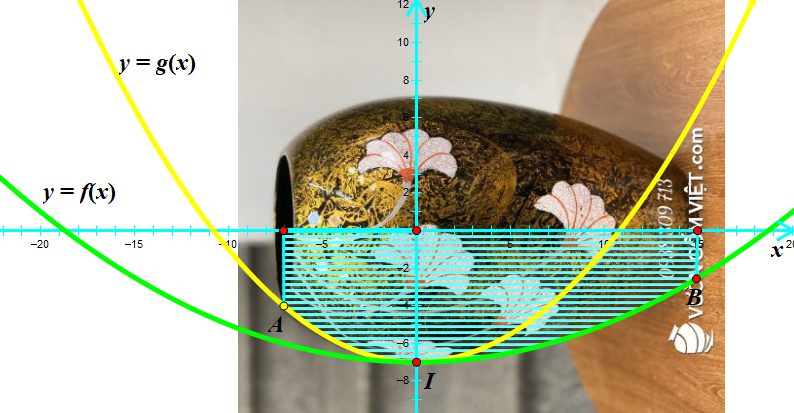
Để tính thể tích lọ gốm, người ta xấp xỉ nó bởi khối tròn xoay sinh bởi phần hình phẳng (phần gạch ngang) giới hạn bởi hai hàm bậc hai \(y = f\left( x \right)\) và \(y = g\left( x \right)\)như hình vẽ. Biết tọa độ đỉnh của hai parabol là \(I\left( {0\,;\, - 7} \right)\), điểm \(A\left( { - 7\,;\, - 4,06} \right)\) thuộc đồ thị \(y = g\left( x \right)\) và điểm \(B\left( … [Đọc thêm...] vềĐể tính thể tích lọ gốm, người ta xấp xỉ nó bởi khối tròn xoay sinh bởi phần hình phẳng (phần gạch ngang) giới hạn bởi hai hàm bậc hai \(y = f\left( x \right)\) và \(y = g\left( x \right)\)như hình vẽ. Biết tọa độ đỉnh của hai parabol là \(I\left( {0\,;\, – 7} \right)\), điểm \(A\left( { – 7\,;\, – 4,06} \right)\) thuộc đồ thị \(y = g\left( x \right)\) và điểm \(B\left( {15\,;\, – 2,5} \right)\) thuộc đồ thị \(y = f\left( x \right)\). Tính thể tích xấp xỉ của lọ gốm (làm tròn đến hàng đơn vị).
Hình vẽ sau thể hiện một vật rắn có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Tính thể tích của vật rắn đó.

Hình vẽ sau thể hiện một vật rắn có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Tính thể tích của vật rắn đó. A. \(\frac{{4\pi \sqrt 3 }}{3}\). B. \(\frac{{4\sqrt 3 }}{3}\). C. \(\frac{{2\sqrt 3 }}{3}\). D. \(\frac{{2\pi \sqrt 3 }}{3}\). Lời giải: Trên mặt phẳng đáy của vật rắn, chọn hệ trục … [Đọc thêm...] vềHình vẽ sau thể hiện một vật rắn có đáy là hình tròn bán kính bằng 1. Các mặt cắt song song, vuông góc với đáy là các tam giác đều. Tính thể tích của vật rắn đó.
Cho hai số thực \(x,y\) không âm thỏa mãn \({x^2} + 2x – y + 1 = {\log _2}\frac{{\sqrt {2y + 1} }}{{x + 1}}\). Khi biếu thức \(P = {e^{2x – 1}} + 4{x^2} – 2y + 1\)đạt giá trị nhỏ nhất, giá trị của biểu thức \(2y – x\) bằng
Cho hai số thực \(x,y\) không âm thỏa mãn \({x^2} + 2x - y + 1 = {\log _2}\frac{{\sqrt {2y + 1} }}{{x + 1}}\). Khi biếu thức \(P = {e^{2x - 1}} + 4{x^2} - 2y + 1\)đạt giá trị nhỏ nhất, giá trị của biểu thức \(2y - x\) bằng A. \(3\). B. \(2\). C. \( - 3\). D. \( - 2\). Lời giải: \({x^2} + 2x - y + 1 = {\log _2}\frac{{\sqrt {2y + 1} }}{{x + 1}}\) \( … [Đọc thêm...] vềCho hai số thực \(x,y\) không âm thỏa mãn \({x^2} + 2x – y + 1 = {\log _2}\frac{{\sqrt {2y + 1} }}{{x + 1}}\). Khi biếu thức \(P = {e^{2x – 1}} + 4{x^2} – 2y + 1\)đạt giá trị nhỏ nhất, giá trị của biểu thức \(2y – x\) bằng
Cho \(2\) số thực \(x,y\) thỏa mãn \({\log _5}{\left[ {(x + 1)\left( {y + 1} \right)} \right]^{y + 1}} = 25 – \left( {x – 1} \right)\left( {y + 1} \right)\). Giá trị nhỏ nhất của biểu thức \(P = x + 3y\) là
Cho \(2\) số thực \(x,y\) thỏa mãn \({\log _5}{\left[ {(x + 1)\left( {y + 1} \right)} \right]^{y + 1}} = 25 - \left( {x - 1} \right)\left( {y + 1} \right)\). Giá trị nhỏ nhất của biểu thức \(P = x + 3y\) là A. \({P_{\min }} = 10\sqrt 3 - 4\). B. \({P_{\min }} = 9\sqrt 3 + 4\). C. \({P_{\min }} = - \sqrt 3 - 4\). D. \({P_{\min }} = 10\sqrt 3 \) Lời giải: Lời … [Đọc thêm...] vềCho \(2\) số thực \(x,y\) thỏa mãn \({\log _5}{\left[ {(x + 1)\left( {y + 1} \right)} \right]^{y + 1}} = 25 – \left( {x – 1} \right)\left( {y + 1} \right)\). Giá trị nhỏ nhất của biểu thức \(P = x + 3y\) là
