[4] Trong không gian \(Oxyz\), cho ba điểm \(A\left( {0;\,3;\, - 5} \right)\), \(B\left( {1;\,1;\, - 5} \right)\), \(C\left( {4;\,3;\, - 1} \right)\) và mặt cầu\(\left( {{S_m}} \right):\) \({x^2} + {y^2} + {z^2} + \left( {m - 2} \right)x + 4y + \left( {m - 2} \right)z - 3 = 0\) (\(m\) là tham số thực). Gọi \(\left( T \right)\) là tập hợp các điểm cố định mà mặt cầu \(\left( … [Đọc thêm...] về[4] Trong không gian \(Oxyz\), cho ba điểm \(A\left( {0;\,3;\, – 5} \right)\), \(B\left( {1;\,1;\, – 5} \right)\), \(C\left( {4;\,3;\, – 1} \right)\) và mặt cầu\(\left( {{S_m}} \right):\) \({x^2} + {y^2} + {z^2} + \left( {m – 2} \right)x + 4y + \left( {m – 2} \right)z – 3 = 0\) (\(m\) là tham số thực). Gọi \(\left( T \right)\) là tập hợp các điểm cố định mà mặt cầu \(\left( {{S_m}} \right)\) luôn đi qua với mọi số thực \(m\) và \(M\) là một điểm di động trên \(\left( T \right)\) sao cho thể tích tứ diện \(MABC\) đạt giá trị lớn nhất \({V_{\max }}\). Giá trị \({V_{\max }}\) bằng
Kết quả tìm kiếm cho: ty so
[4] Trong không gian \(Oxyz\) cho hình nón \(\left( N \right)\)có đỉnh \(S\left( {4;5; – 3} \right)\), bán kính đáy \({\rm{12 }}\)và đường tròn đáy nằm trên mặt phẳng \(\left( P \right):x + 2y – 2z + 28 = 0\). Khi cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần với giá trị nào sau đây?
[4] Trong không gian \(Oxyz\) cho hình nón \(\left( N \right)\)có đỉnh \(S\left( {4;5; - 3} \right)\), bán kính đáy \({\rm{12 }}\)và đường tròn đáy nằm trên mặt phẳng \(\left( P \right):x + 2y - 2z + 28 = 0\). Khi cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần với giá trị nào sau đây? A. \(170\). B. … [Đọc thêm...] về[4] Trong không gian \(Oxyz\) cho hình nón \(\left( N \right)\)có đỉnh \(S\left( {4;5; – 3} \right)\), bán kính đáy \({\rm{12 }}\)và đường tròn đáy nằm trên mặt phẳng \(\left( P \right):x + 2y – 2z + 28 = 0\). Khi cắt hình nón bởi một mặt phẳng song song với đường sinh của hình nón ta thu được thiết diện có diện tích lớn nhất gần với giá trị nào sau đây?
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f’\left( x \right) = \left( {{x^2} – 9} \right)\left( {x – 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} – m} \right)\) có đúng \(7\) điểm cực trị
[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 9} \right)\left( {x - 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} - m} \right)\) có đúng \(7\) điểm cực trị A. \(3\) B. \(4\) C. \(5\) D. \(6\) Lời giải: Ta có \(g'\left( x … [Đọc thêm...] về[Mức độ 4] Cho hàm số \(y = f\left( x \right)\), có đạo hàm \(f’\left( x \right) = \left( {{x^2} – 9} \right)\left( {x – 5} \right).\) Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) sao cho hàm số \(g\left( x \right) = f\left( {{e^{{x^3} + 3{x^2}}} – m} \right)\) có đúng \(7\) điểm cực trị
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
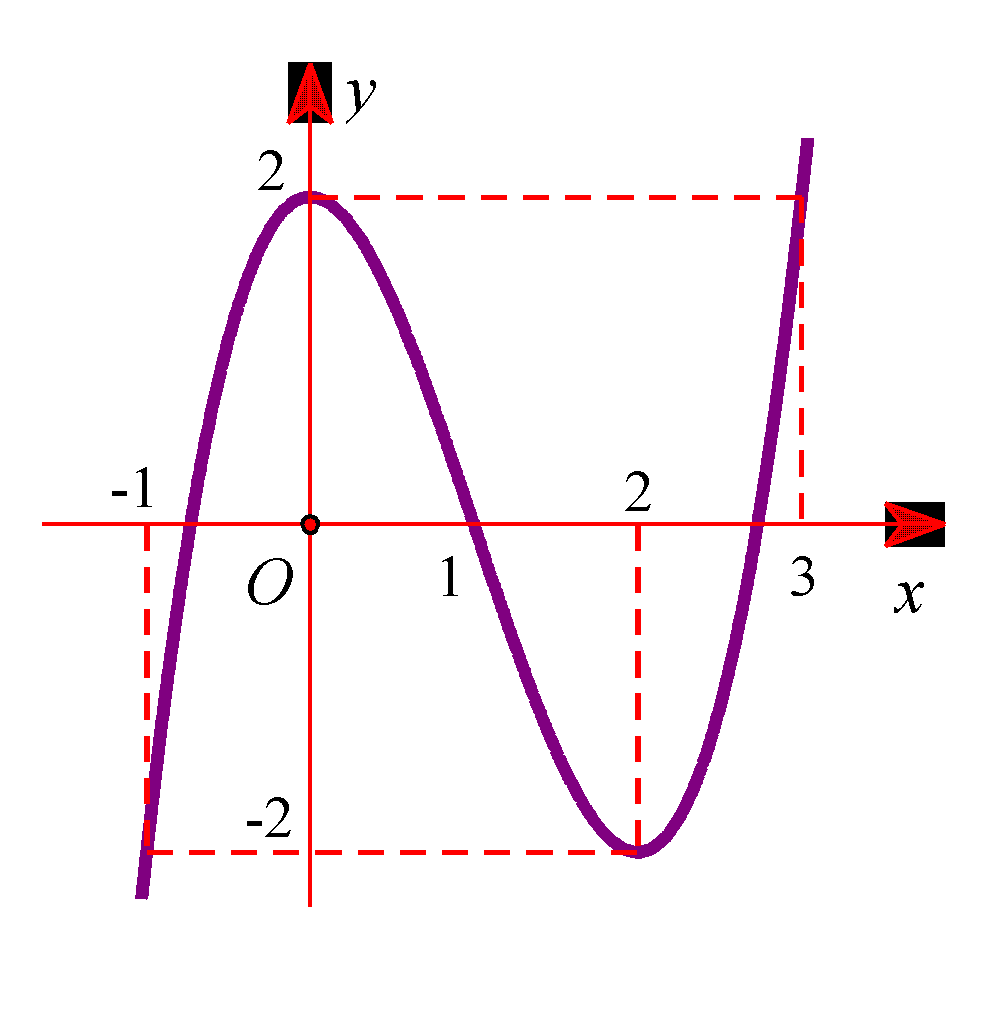
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x - m} \right) - \frac{1}{2}{\left( {x - m - 1} \right)^2} + 2022\), với \(m\) là tham số thự C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng … [Đọc thêm...] về[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} – 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} – 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
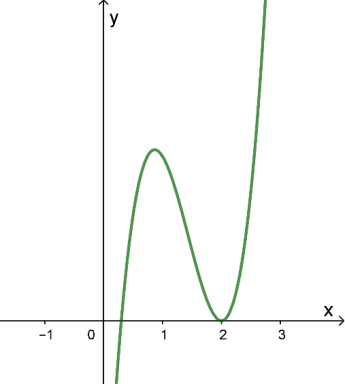
[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} - 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} - 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng? A. 4. B. 3. C. 2. D. 6. Lời giải: Quan sát đồ thị hàm số … [Đọc thêm...] về[Mức độ 4] Cho hàm số bậc ba \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số \(g\left( x \right) = \frac{{\left( {{x^2} – 3x + 2} \right)\sqrt {2x + 1} }}{{\left( {{x^4} – 5{x^2} + 4} \right).f\left( x \right)}}\) có bao nhiêu đường tiệm cận đứng?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có \(f\left( 5 \right) > 8\) và \(f\left( 1 \right) = 0.\) Biết hàm số
\(y = f’\left( x \right)\) có đồ thị như hình vẽ bên.
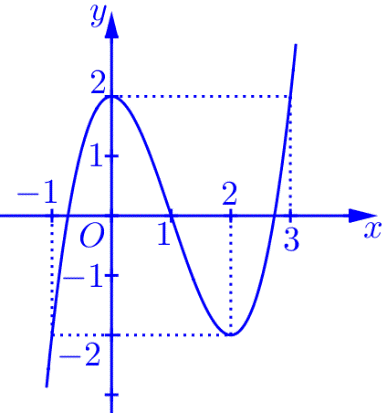
Hàm số \(g\left( x \right) = \left| {f\left( {1 – \frac{x}{2}} \right) – \frac{{{x^2}}}{8}} \right|\) nghịch biến trên khoảng nào dưới đây?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có \(f\left( 5 \right) > 8\) và \(f\left( 1 \right) = 0.\) Biết hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(g\left( x \right) = \left| {f\left( {1 - \frac{x}{2}} \right) - \frac{{{x^2}}}{8}} \right|\) nghịch biến trên khoảng nào dưới đây? A. \(\left( { - 8; - 4} \right)\). B. … [Đọc thêm...] về[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có \(f\left( 5 \right) > 8\) và \(f\left( 1 \right) = 0.\) Biết hàm số
\(y = f’\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số \(g\left( x \right) = \left| {f\left( {1 – \frac{x}{2}} \right) – \frac{{{x^2}}}{8}} \right|\) nghịch biến trên khoảng nào dưới đây?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ sau.
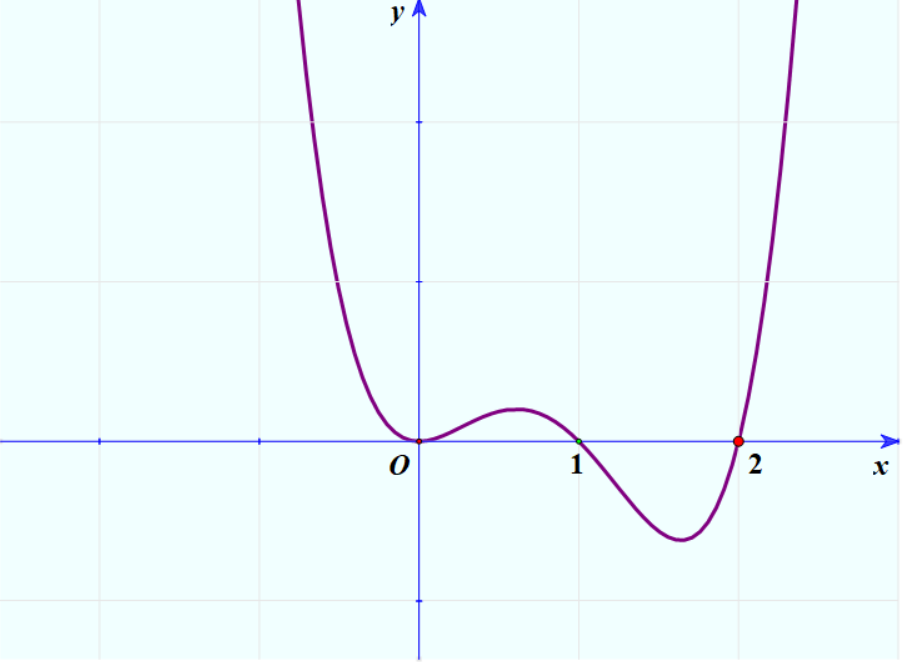
Hỏi đồ thị hàm số \(y = \frac{{{f^2}\left( x \right)\sqrt {{x^2} + x} }}{{\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]\left( {2{x^5} + {x^4} – 10{x^3} – 5{x^2} + 8x + 4} \right)}}\) có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Hỏi đồ thị hàm số \(y = \frac{{{f^2}\left( x \right)\sqrt {{x^2} + x} }}{{\left[ {{f^2}\left( x \right) - 2f\left( x \right)} \right]\left( {2{x^5} + {x^4} - 10{x^3} - 5{x^2} + 8x + 4} \right)}}\) có bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. \(7\). B. \(6\). C. … [Đọc thêm...] về[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ sau.
Hỏi đồ thị hàm số \(y = \frac{{{f^2}\left( x \right)\sqrt {{x^2} + x} }}{{\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]\left( {2{x^5} + {x^4} – 10{x^3} – 5{x^2} + 8x + 4} \right)}}\) có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ:

Hàm số \(y = f\left( {3 – 2{x^2}} \right)\) đồng biến trên khoảng nào dưới đây?
Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ: Hàm số \(y = f\left( {3 - 2{x^2}} \right)\) đồng biến trên khoảng nào dưới đây? A. \(\left( { - \infty ;0} \right)\). B. \(\left( {0;1} \right)\). C. \(\left( { - \frac{{\sqrt 2 }}{2};0} \right)\). D. \(\left( {1;2} \right)\). Lời giải: Hàm số \(y = f\left( {3 - 2{x^2}} \right)\) có … [Đọc thêm...] vềMức độ 3] Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ:
Hàm số \(y = f\left( {3 – 2{x^2}} \right)\) đồng biến trên khoảng nào dưới đây?
[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 5 \right) = 3\) . Hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên dưới:

Số nghiệm thực của phương trình \(f\left( x \right) = 4\) là
[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 5 \right) = 3\) . Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên dưới: Số nghiệm thực của phương trình \(f\left( x \right) = 4\) là A. 5 B. 2 C. 3 D. 4 Lời giải: Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi \(y = f'\left( x \right);y = … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 5 \right) = 3\) . Hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình \(f\left( x \right) = 4\) là
Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của \(f’\left( x \right)\) như sau:

Hàm số \(y = f\left( {{x^2} – x} \right)\) đồng biến trên khoảng nào dưới đây?
Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của \(f'\left( x \right)\) như sau: Hàm số \(y = f\left( {{x^2} - x} \right)\) đồng biến trên khoảng nào dưới đây? A. \(\left( {1;2} \right)\). B. \(\left( {3; + \infty } \right)\). C. \(\left( { + \infty ;1} \right)\). D. \(\left( { - 1;3} \right)\). Lời giải: Ta có \(y' = \left[ {f\left( … [Đọc thêm...] vềMức độ 3] Cho hàm số \(y = f\left( x \right)\) có bảng xét dấu của \(f’\left( x \right)\) như sau:
Hàm số \(y = f\left( {{x^2} – x} \right)\) đồng biến trên khoảng nào dưới đây?
