Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Cho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau.

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:,

Cho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau. Số điểm cực trị của hàm số \(g\left( x \right) = \frac{1}{{{x^4}}}{\left[ {f\left( x \right) - 1} \right]^4}\) là A. \(6\) . B. \(5\). C. \(4\). D. \(7\). Lời giải Từ BBT của hàm số bậc bốn trùng phương \(f\left( x \right) = a{x^4} + b{x^2} + c\) ta thấy đồ thị hàm số nhận điểm có tọa độ … [Đọc thêm...] vềCho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau.

Cho hàm số f(x) có f(0) = 0. Biết y = f'(x) là hàm số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^4}} \right) – {x^2}} \right|\)

Ngày Thuộc chủ đề:Trắc nghiệm Cực trị của hàm số Tag với:,

Câu hỏi: Cho hàm số f(x) có f(0) = 0. Biết y = f'(x) là hàm số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^4}} \right) - {x^2}} \right|\) là A. 4 B.3 C.6 D.5 ======== Đáp án đúng: D Xét hàm số \(h\left( x \right) = f\left( {{x^4}} \right) - {x^2}\) có \(h'\left( x \right) = … [Đọc thêm...] vềCho hàm số f(x) có f(0) = 0. Biết y = f'(x) là hàm số bậc bốn và có đồ thị như hình vẽ. Số điểm cực trị của hàm số \(g\left( x \right) = \left| {f\left( {{x^4}} \right) – {x^2}} \right|\)

Cho hàm số y =f(x) có bảng xét dấu đạo hàm như hình vẽ. Hàm số \(y=2 f(1-x)+\sqrt{x^{2}+1}-x\) nghịch biến trên khoảng nào:

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Cho hàm số y =f(x) có bảng xét dấu đạo hàm như hình vẽ Hàm số \(y=2 f(1-x)+\sqrt{x^{2}+1}-x\) nghịch biến trên khoảng nào: A. \((-\infty ; 1)\) B. \((-\infty ;-2)\) C. \((-3 ;-2)\) D. \((-2 ; 0)\) ======== \(y^{\prime}=-2 f^{\prime}(1-x)+\frac{x}{\sqrt{x^{2}+1}}-1<0\) Ta có \(\frac{x}{\sqrt{x^{2}+1}}-1<0, \forall x \in \mathbb{R}\) Khi \(1<1-x<3 … [Đọc thêm...] vềCho hàm số y =f(x) có bảng xét dấu đạo hàm như hình vẽ. Hàm số \(y=2 f(1-x)+\sqrt{x^{2}+1}-x\) nghịch biến trên khoảng nào:

Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số\(f (x)=m^{2}\left(\frac{e^{5 x}}{5}-16 e^{x}\right)+3 m\left(\frac{e^{3 x}}{3}-4 e^{x}\right)-14\left(\frac{e^{2 x}}{2}-2 e^{x}\right)+2020\) đồng biến trên \(\mathbb{R}\) . Tổng của tất cả các phần tử thuộc S bằng:

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Gọi S là tập hợp tất cả các giá trị của tham số m để hàm số\(f (x)=m^{2}\left(\frac{e^{5 x}}{5}-16 e^{x}\right)+3 m\left(\frac{e^{3 x}}{3}-4 e^{x}\right)-14\left(\frac{e^{2 x}}{2}-2 e^{x}\right)+2020\) đồng biến trên \(\mathbb{R}\) . Tổng của tất cả các phần tử thuộc S bằng: A. \(-\frac{7}{8}\)B. \(\frac{1}{2}\)C. \( -2\)D. … [Đọc thêm...] vềGọi S là tập hợp tất cả các giá trị của tham số m để hàm số\(f (x)=m^{2}\left(\frac{e^{5 x}}{5}-16 e^{x}\right)+3 m\left(\frac{e^{3 x}}{3}-4 e^{x}\right)-14\left(\frac{e^{2 x}}{2}-2 e^{x}\right)+2020\) đồng biến trên \(\mathbb{R}\) . Tổng của tất cả các phần tử thuộc S bằng:

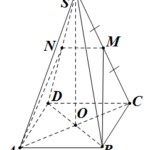
Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5}  cm$, đường chéo $AC=4  cm$. Đoạn thẳng $SO=2\sqrt{2}  cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$

Ngày Thuộc chủ đề:Hình học không gian Tag với:

Đề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5}  cm$, đường chéo $AC=4  cm$. Đoạn thẳng $SO=2\sqrt{2}  cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$ Lời giải Normal 0 false … [Đọc thêm...] vềĐề bài: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng $\sqrt{5}  cm$, đường chéo $AC=4  cm$. Đoạn thẳng $SO=2\sqrt{2}  cm$ và vuông góc với đáy, ở tâm $O$ là giao điểm của hai đường chéo $AC, BD$. Gọi $M$ là trung điểm của cạnh $SC$. Giả sử mặt phẳng $(ABM)$ cắt $SD$ tại $N$. Tìm thể tích khối chóp $S.ABMN$

[VDC LOG 2020] Cho các số thực dương a, b thỏa mãn \({\log _4}a = {\log _6}b = {\log _9}\left( {4a – 5b} \right) – 1\). Đặt \(T = \frac{b}{a}\). Khẳng định nào sau đây đúng?

Ngày Thuộc chủ đề:Trắc nghiệm Logarit và hàm số lôgarit Tag với:,

Câu hỏi: Cho các số thực dương a, b thỏa mãn \({\log _4}a = {\log _6}b = {\log _9}\left( {4a - 5b} \right) - 1\). Đặt \(T = \frac{b}{a}\). Khẳng định nào sau đây đúng? A. 1 B. \(\frac{1}{2}\) C. - 2 D. 0 Lời giải tham khảo: Hãy chọn trả lời đúng trước khi xem đáp án và lời giải bên dưới. Đáp án đúng: B \(\begin{array}{l} {\log … [Đọc thêm...] về[VDC LOG 2020] Cho các số thực dương a, b thỏa mãn \({\log _4}a = {\log _6}b = {\log _9}\left( {4a – 5b} \right) – 1\). Đặt \(T = \frac{b}{a}\). Khẳng định nào sau đây đúng?

[Dạng câu 50 Toán L2 – 2020] Có bao nhiêu cặp số nguyên dương \(\left( {x,y} \right)\) thỏa \(1 < x \le 100\)và \({\log _2}\left( {y + \sqrt {x + y} } \right).{\log _x}2 = 2\)?

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:

  Có bao nhiêu cặp số nguyên dương \(\left( {x,y} \right)\) thỏa \(1 < x \le 100\) và \({\log _2}\left( {y + \sqrt {x + y} } \right).{\log _x}2 = 2\)? A. 99 B. 98 C. 10 D. 90 Lời giải Ta có \({\log _2}\left( {y + \sqrt {x + y} } \right).{\log _x}2 = 2 \Leftrightarrow {\log _2}\left( {y + \sqrt {x + y} } \right) = \frac{2}{{{{\log }_x}2}}\) \( … [Đọc thêm...] về[Dạng câu 50 Toán L2 – 2020] Có bao nhiêu cặp số nguyên dương \(\left( {x,y} \right)\) thỏa \(1 < x \le 100\)và \({\log _2}\left( {y + \sqrt {x + y} } \right).{\log _x}2 = 2\)?

[Trắc nghiệm VD-VDC Toán 2020] Câu 43:Cho phương trình \(\log _3^23x + {\log _3}x + m – 1 = 0\) (với là \(m\) tham số thực). Tập hợp tất cả các giá trị của \(m\) để phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng \[{\rm{(0 ; 1)}}\] là khoảng nào dưới đây?

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:

[Trắc nghiệm VD-VDC Toán 2020] Câu 43:Cho phương trình \(\log _3^23x + {\log _3}x + m - 1 = 0\) (với là \(m\) tham số thực). Tập hợp tất cả các giá trị của \(m\) để phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng \[{\rm{(0 ; 1)}}\] là khoảng nào dưới đây? \(\left( { - \infty ; - \frac{9}{4}} \right)\). B. \(\left( {\frac{9}{4}; + \infty } \right)\). C. \(\left( … [Đọc thêm...] về[Trắc nghiệm VD-VDC Toán 2020] Câu 43:Cho phương trình \(\log _3^23x + {\log _3}x + m – 1 = 0\) (với là \(m\) tham số thực). Tập hợp tất cả các giá trị của \(m\) để phương trình đã cho có đúng 2 nghiệm phân biệt thuộc khoảng \[{\rm{(0 ; 1)}}\] là khoảng nào dưới đây?

[Trắc nghiệm VD-VDC Toán 2020] Câu 43:Tất cả các giá trị thực của tham số \(m\) để phương trình \({9^x} – 2(2m + 1) \cdot {3^x} + 3(4m – 1) = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mản \(\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 12\) thuộc khoảng nào dưới đây?

Ngày Thuộc chủ đề:Trắc nghiệm Phương trình và bất phương trình Logarit Tag với:

[Trắc nghiệm VD-VDC Toán 2020] Câu 43:Tất cả các giá trị thực của tham số \(m\) để phương trình \({9^x} - 2(2m + 1) \cdot {3^x} + 3(4m - 1) = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mản \(\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 12\) thuộc khoảng nào dưới đây? \(\left( {3;9} \right)\). B. \(\left( {9; + \infty } \right)\). C. \[\left( {\frac{1}{4};3} … [Đọc thêm...] về[Trắc nghiệm VD-VDC Toán 2020] Câu 43:Tất cả các giá trị thực của tham số \(m\) để phương trình \({9^x} – 2(2m + 1) \cdot {3^x} + 3(4m – 1) = 0\) có hai nghiệm \({x_1},{x_2}\) thỏa mản \(\left( {{x_1} + 2} \right)\left( {{x_2} + 2} \right) = 12\) thuộc khoảng nào dưới đây?