Cho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau.

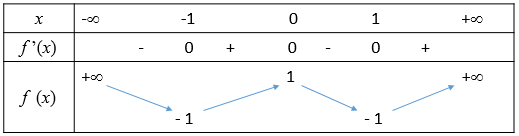
Cho hàm số bậc bốn trùng phương \(f\left( x \right)\) có bảng biến thiên như sau.

Số điểm cực trị của hàm số \(g\left( x \right) = \frac{1}{{{x^4}}}{\left[ {f\left( x \right) – 1} \right]^4}\) là
A. \(6\) .

B. \(5\).

C. \(4\).

D. \(7\).

Lời giải

Từ BBT của hàm số bậc bốn trùng phương \(f\left( x \right) = a{x^4} + b{x^2} + c\) ta thấy đồ thị hàm số nhận điểm có tọa độ \(\left( {0;1} \right);\left( { \pm 1; – 1} \right)\) là các điểm cực trị nên
\(\left\{ \begin{array}{l}f\left( 0 \right) = 1\\f\left( { \pm 1} \right) = – 1\\f’\left( { \pm 1} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b + c = – 1\\4a + 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = – 4\\c = 1\end{array} \right. \Rightarrow f\left( x \right) = 2{x^4} – 4{x^2} + 1\)
Khi đó hàm số \(g\left( x \right) = {\left[ {2{x^3} – 4x} \right]^4}\) có TXĐ: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
\(g’\left( x \right) = 4{\left[ {2{x^3} – 4x} \right]^3}\left( {6{x^2} – 4} \right) = 4{x^3}{\left[ {2{x^2} – 4} \right]^3}\left( {6{x^2} – 4} \right)\)
Ta thấy \(g’\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \\x = \pm \sqrt {\frac{2}{3}} \end{array} \right.\).
Ta thấy \(g’\left( x \right)\) đổi dấu khi qua các nghiệm \(\left[ \begin{array}{l}x = 0\\x = \pm \sqrt 2 \\x = \pm \sqrt {\frac{2}{3}} \end{array} \right.\) nhưng nghiệm \(x = 0\) không thuộc tập xác định của hàm số \(g\left( x \right)\)nên hàm số \(g\left( x \right)\) có 4 cực trị.