Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

Xét tính đúng sai của các phát biểu sau:

Bài toán gốc

Câu 15. Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây:

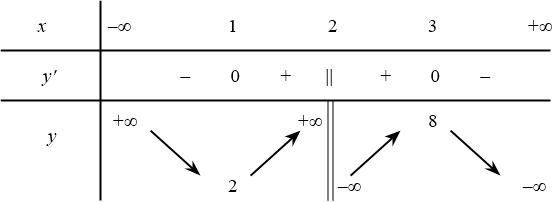
Xét tính đúng sai của các phát biểu sau:

a) Hàm số $y=f(x)$ có hai điểm cực trị.

b) Hàm số $y=f(x)$ đạt điểm cực đại tại điểm $x=1$.

c) Hàm số $y=f(x)$ không điểm cực trị.

d) Hàm số $y=f(x)$ có tổng các giá trị cực trị bằng $10$.

Lời giải:
(Đúng) Hàm số $y=f(x)$ có hai điểm cực trị.
(Sai) Hàm số $y=f(x)$ đạt điểm cực đại tại điểm $x=1$.
(Sai) Hàm số $y=f(x)$ không điểm cực trị.
(Đúng) Hàm số $y=f(x)$ có tổng các giá trị cực trị bằng $10$.
(Vì): Tổng các cực trị của hàm số bằng $2+8=10$.

Phân tích và Phương pháp giải

Đây là dạng bài toán phân tích các tính chất về cực trị (điểm cực đại, điểm cực tiểu, giá trị cực đại, giá trị cực tiểu) của hàm số dựa trên bảng biến thiên của hàm số và đạo hàm của nó ($f'(x)$). Phương pháp giải là dựa vào quy tắc: Nếu $f'(x)$ đổi dấu từ dương sang âm khi qua điểm $x_0$, hàm số đạt cực đại tại $x_0$. Nếu $f'(x)$ đổi dấu từ âm sang dương khi qua điểm $x_0$, hàm số đạt cực tiểu tại $x_0$. Giá trị tương ứng của $f(x)$ là giá trị cực trị.

Bài toán tương tự

Cho hàm số $y=f(x)$ có bảng biến thiên như sau: (Hàm số xác định trên $\mathbb{R}$)

| x | $-\infty$ | -1 | 2 | $+\infty$ |

|—|—|—|—|—|

| $f'(x)$ | | + | 0 | – | 0 | + |

| $f(x)$ | $-\infty$ | $\nearrow$ | 7 | $\searrow$ | 3 | $\nearrow$ | $+\infty$ |

Hỏi hàm số $y=f(x)$ có tổng các giá trị cực trị là bao nhiêu?

A. 4

B. 10

C. 7

D. 3

Đáp án đúng: B.

Lời giải ngắn gọn: Dựa vào bảng biến thiên:

– Tại $x=-1$, $f'(x)$ đổi dấu từ (+) sang (-), nên $x=-1$ là điểm cực đại và giá trị cực đại là $y_{CĐ} = 7$.

– Tại $x=2$, $f'(x)$ đổi dấu từ (-) sang (+), nên $x=2$ là điểm cực tiểu và giá trị cực tiểu là $y_{CT} = 3$.

Tổng các giá trị cực trị là $7 + 3 = 10$.