Cho hàm số $y=f(x)=\dfrac{-2x^2-3x+1}{-x-3}$. Xét tính đúng sai của các phát biểu sau:

a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{3\right\}$.

Bài toán gốc

Câu 21. Cho hàm số $y=f(x)=\dfrac{-2x^2-3x+1}{-x-3}$. Xét tính đúng sai của các phát biểu sau:

a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{3\right\}$.

b) $y^{\prime}=\dfrac{2x^2+12x+10}{(-x-3)^2}$.

c) Hàm số $y=f(x)$ có tổng các giá trị cực trị bằng $-18$.

d) Hàm số $y=f(2x+12)$ có tổng giá trị cực đại và cực tiểu bằng $-18$.

Lời giải: $y^{\prime}=\dfrac{2x^2+12x+10}{(-x-3)^2}$.
$y^{\prime}=0\Leftrightarrow x_1=-5,x_2=-1$.

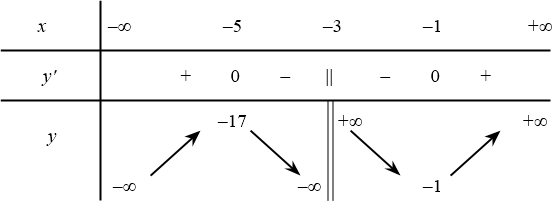
(Sai) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{3\right\}$.
(Vì): $-x-3\neq 0\Leftrightarrow x\neq -3$ nên $D=\mathbb{R}\backslash \left\{-3\right\}$.
(Đúng) $y^{\prime}=\dfrac{2x^2+12x+10}{(-x-3)^2}$.
(Đúng) Hàm số $y=f(x)$ có tổng các giá trị cực trị bằng $-18$.
(Vì): Tổng các cực trị của hàm số bằng $-17-1=-18$.
(Đúng) Hàm số $y=f(2x+12)$ có tổng giá trị cực đại và cực tiểu bằng $-18$.
(Vì): $-17-1=-18$.
Hàm số $y=f(x)$ và hàm số $y=f(ax+b)$ có cùng số điểm cực trị, cùng số điểm cực đại, cùng số điểm cực tiểu. Biến điểm cực đại thành điểm cực đại, biến điểm cực tiểu thành điểm cực tiểu. Có giá trị cực đại bằng nhau và giá trị cực tiểu bằng nhau tương ứng.

PHẦN III. Câu trắc nghiệm trả lời ngắn

Phân tích và Phương pháp giải

Bài toán gốc yêu cầu kiểm tra tính đúng sai của các phát biểu liên quan đến hàm số hữu tỉ $y=f(x)=\frac{P(x)}{Q(x)}$. Các bước giải quyết bao gồm: 1. Xác định Tập xác định (Dựa vào mẫu số khác 0). 2. Tính đạo hàm $y’$ bằng công thức đạo hàm của thương. 3. Tìm các điểm cực trị bằng cách giải phương trình $y’=0$ và tính các giá trị cực trị tương ứng. 4. Áp dụng quy tắc về giá trị cực trị của hàm hợp $y=f(ax+b)$, trong đó giá trị cực trị của hàm hợp bằng giá trị cực trị của hàm số gốc $y=f(x)$.

Bài toán tương tự

Cho hàm số $y=g(x)=\dfrac{x^2+x+4}{x+1}$. Xét tính đúng sai của các phát biểu sau:\a) Hàm số $y=g(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{1\right\}$.\b) $g^{\prime}(x)=\dfrac{x^2+2x-3}{(x+1)^2}$.\c) Hàm số $y=g(x)$ có tổng các giá trị cực trị bằng $5$.\d) Hàm số $y=g(3x-5)$ có tổng giá trị cực đại và cực tiểu bằng $-2$.Đáp án và Lời giải ngắn gọn:Ta có: $g(x)=\dfrac{x^2+x+4}{x+1}$.\* Tập xác định: $x+1\neq 0 \Leftrightarrow x\neq -1$. $D=\mathbb{R}\backslash \left\{-1\right\}$. (Phát biểu a là SAI).\* Đạo hàm: $g'(x) = \frac{(2x+1)(x+1) – (x^2+x+4)(1)}{(x+1)^2} = \frac{2x^2+3x+1 – x^2-x-4}{(x+1)^2} = \frac{x^2+2x-3}{(x+1)^2}$. (Phát biểu b là ĐÚNG).\* Cực trị: $g'(x)=0 \Leftrightarrow x^2+2x-3=0 \Leftrightarrow x=1$ hoặc $x=-3$.\$g(1) = \dfrac{1^2+1+4}{1+1} = 3$. $g(-3) = \dfrac{(-3)^2+(-3)+4}{-3+1} = -5$.Các giá trị cực trị là $3$ (cực tiểu) và $-5$ (cực đại). Tổng các giá trị cực trị là $3 + (-5) = -2$. (Phát biểu c là SAI).\* Hàm hợp: Hàm số $y=g(3x-5)$ có tổng giá trị cực đại và cực tiểu bằng tổng giá trị cực trị của $y=g(x)$, tức là $-2$. (Phát biểu d là ĐÚNG).Kết luận: Các phát biểu đúng là b) và d).