Cho hàm số $y=f(x)=\dfrac{-3x^2-x+5}{-x+5}$. Xét tính đúng sai của các phát biểu sau:

Bài toán gốc

Câu 11. Cho hàm số $y=f(x)=\dfrac{-3x^2-x+5}{-x+5}$. Xét tính đúng sai của các phát biểu sau:

a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{5\right\}$. b) $y^{\prime}=\dfrac{3x^2-30x-16}{(-x+5)^2}$.

c) $y^{\prime}=0\Leftrightarrow x_1=0,x_2=5$. d) Hàm số $y=f(x)$ không điểm cực trị.

Lời giải: $y^{\prime}=\dfrac{3x^2-30x}{(-x+5)^2}$.
$y^{\prime}=0\Leftrightarrow x_1=0,x_2=10$.

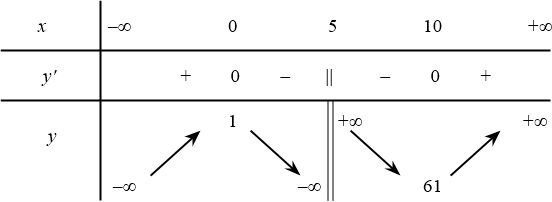
(Đúng) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{5\right\}$.
(Vì): $-x+5\neq 0\Leftrightarrow x\neq 5$ nên $D=\mathbb{R}\backslash \left\{5\right\}$.
(Sai) $y^{\prime}=\dfrac{3x^2-30x-16}{(-x+5)^2}$.
(Vì): $y^{\prime}=\dfrac{adx^2+2aex+be-cd}{(dx+e)^2}=\dfrac{3x^2-30x}{(-x+5)^2}$.
(Sai) $y^{\prime}=0\Leftrightarrow x_1=0,x_2=5$.
(Sai) Hàm số $y=f(x)$ không điểm cực trị.

Phân tích và Phương pháp giải

Đây là dạng bài tập phân tích các tính chất cơ bản của hàm số hữu tỉ bậc hai trên bậc nhất ($y = \frac{ax^2 + bx + c}{dx + e}$). Phương pháp giải bao gồm: 1. Xác định tập xác định bằng cách loại trừ nghiệm của mẫu số. 2. Tính đạo hàm bằng công thức đạo hàm của thương. 3. Tìm điểm cực trị bằng cách giải phương trình $y’=0$ và so sánh nghiệm với tập xác định.

Bài toán tương tự

Cho hàm số $y=f(x)=\dfrac{x^2+3x-1}{x-2}$. Xét tính đúng sai của các phát biểu sau:
a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{2\right\}$.
b) $y^{\prime}=\dfrac{x^2-4x-5}{(x-2)^2}$.
c) Hàm số $y=f(x)$ chỉ có một điểm cực trị.
d) $y^{\prime}=0$ có nghiệm $x_1=-1$ và $x_2=5$.