Cho hàm số $y=f(x)=-2x^3+15x^2-24x+2$. Xét tính đúng sai của các phát biểu sau:

a) $y^{\prime}=-6x^2+30x-24$.

Bài toán gốc

Câu 18. Cho hàm số $y=f(x)=-2x^3+15x^2-24x+2$. Xét tính đúng sai của các phát biểu sau:

a) $y^{\prime}=-6x^2+30x-24$.

b) Đồ thị hàm số đạt cực tiểu tại điểm $M(4;18)$.

c) Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình $y=9x-18$.

d) Hàm số $y=f(-3x-3)$ có tổng giá trị cực đại và cực tiểu bằng $5$.

Lời giải: $y^{\prime}=-6x^2+30x-24$
$y^{\prime}=0\Leftrightarrow x_1=1,x_2=4$.

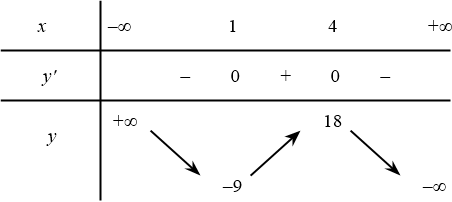
(Đúng) $y^{\prime}=-6x^2+30x-24$.
(Sai) Đồ thị hàm số đạt cực tiểu tại điểm $M(4;18)$.
(Đúng) Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình $y=9x-18$.
(Vì): gọi $A\left( {{x}_{1}};{{y}_{1}} \right),B\left( {{x}_{2}};{{y}_{2}} \right)$ là hai điểm cực trị của đồ thị hàm số thì đường thẳng $AB:y=\dfrac{{{y}_{1}}-{{y}_{2}}}{{{x}_{1}}-{{x}_{2}}}\left( x-{{x}_{1}} \right)+{{y}_{1}}$.
(Sai) Hàm số $y=f(-3x-3)$ có tổng giá trị cực đại và cực tiểu bằng $5$.
(Vì): $-9+18=9$.
Hàm số $y=f(x)$ và hàm số $y=f(ax+b)$ có cùng số điểm cực trị, cùng số điểm cực đại, cùng số điểm cực tiểu. Biến điểm cực đại thành điểm cực đại, biến điểm cực tiểu thành điểm cực tiểu. Có giá trị cực đại bằng nhau và giá trị cực tiểu bằng nhau tương ứng.

Phân tích và Phương pháp giải

Bài toán yêu cầu kiểm tra các tính chất của hàm số bậc ba, bao gồm: tính đạo hàm, xác định các điểm cực trị (cực đại, cực tiểu), viết phương trình đường thẳng đi qua hai điểm cực trị, và nhận diện sự thay đổi của giá trị cực trị khi biến đổi biến số ($y=f(ax+b)$). Phương pháp giải bao gồm việc tính đạo hàm $y’$, tìm nghiệm của $y’=0$ để xác định hoành độ cực trị, sử dụng bảng biến thiên hoặc dấu của đạo hàm cấp hai để xác định tính chất cực trị, và áp dụng công thức tìm phương trình đường thẳng đi qua hai điểm cực trị. Đặc biệt, cần nhớ rằng hàm số $y=f(ax+b)$ có giá trị cực đại và cực tiểu bằng với hàm số $y=f(x)$.

Bài toán tương tự

Cho hàm số $y=f(x)=x^3-6x^2+9x-1$. Xét tính đúng sai của các phát biểu sau: a) $y^{\prime}=3x^2-12x+9$. b) Đồ thị hàm số đạt cực đại tại điểm $A(1; 3)$. c) Đường thẳng qua hai điểm cực trị của đồ thị hàm số có phương trình $y=-2x+5$. d) Hàm số $y=f(2x+1)$ có tích giá trị cực đại và cực tiểu bằng $-3$.

Đáp án và Lời giải ngắn gọn:
Tất cả các phát biểu (a), (b), (c), (d) đều ĐÚNG.
1. Đạo hàm: $y^{\prime}=3x^2-12x+9$. (a) Đúng.
2. Cực trị: $y^{\prime}=0 \Leftrightarrow 3(x-1)(x-3)=0 \Leftrightarrow x_1=1, x_2=3$.
$f(1) = 3$ (Cực đại), $f(3) = -1$ (Cực tiểu). Điểm cực đại là $A(1; 3)$. (b) Đúng.
3. Đường thẳng qua cực trị: Hai điểm cực trị là $A(1; 3)$ và $B(3; -1)$. Hệ số góc $m = (-1 – 3) / (3 – 1) = -2$. Phương trình: $y – 3 = -2(x – 1) \Rightarrow y = -2x + 5$. (c) Đúng.
4. Giá trị cực trị của $f(2x+1)$ là $V_{max}=3$ và $V_{min}=-1$. Tích giá trị cực đại và cực tiểu là $3 \times (-1) = -3$. (d) Đúng.