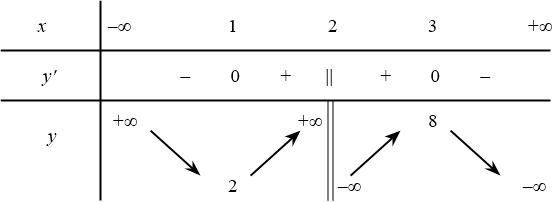
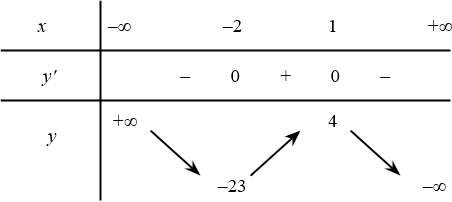
Bài toán gốc Câu 21. Cho hàm số $y=f(x)=\dfrac{-2x^2-3x+1}{-x-3}$. Xét tính đúng sai của các phát biểu sau:a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{3\right\}$.b) $y^{\prime}=\dfrac{2x^2+12x+10}{(-x-3)^2}$.c) Hàm số $y=f(x)$ có tổng các giá trị cực trị bằng $-18$.d) Hàm số $y=f(2x+12)$ có tổng giá trị cực đại và cực tiểu bằng $-18$.Lời giải: … [Đọc thêm...] vềCho hàm số $y=f(x)=\dfrac{-2x^2-3x+1}{-x-3}$. Xét tính đúng sai của các phát biểu sau:
a) Hàm số $y=f(x)$ có tập xác định $D=\mathbb{R}\backslash \left\{3\right\}$.