Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: dơ số 4 và số 2

Một tàu ngầm hạt nhân do ông Nhẫn thiết kế có dạng (như hình minh họa) biết rằng đầu tàu và đuôi tàu có dạng là hình bán cầu, thân tàu có dạng là một hình trụ. Tổng chiều dài thân tàu là \(29,6\,{\rm{m}}\)và chiều cao của thân tàu là \({\rm{8,4}}\,{\rm{m}}\). Tính thể tích của con tàu chính xác tới hàng phần trăm.Nga tiếp tục phát triển dự án tàu ngầm mini

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Một tàu ngầm hạt nhân do ông Nhẫn thiết kế có dạng (như hình minh họa) biết rằng đầu tàu và đuôi tàu có dạng là hình bán cầu, thân tàu có dạng là một hình trụ. Tổng chiều dài thân tàu là \(29,6\,{\rm{m}}\)và chiều cao của thân tàu là \({\rm{8,4}}\,{\rm{m}}\). Tính thể tích của con tàu chính xác tới hàng phần trăm. A. \(7182,13\,{{\rm{m}}^{\rm{3}}}\). B. … [Đọc thêm...] vềMột tàu ngầm hạt nhân do ông Nhẫn thiết kế có dạng (như hình minh họa) biết rằng đầu tàu và đuôi tàu có dạng là hình bán cầu, thân tàu có dạng là một hình trụ. Tổng chiều dài thân tàu là \(29,6\,{\rm{m}}\)và chiều cao của thân tàu là \({\rm{8,4}}\,{\rm{m}}\). Tính thể tích của con tàu chính xác tới hàng phần trăm.Nga tiếp tục phát triển dự án tàu ngầm mini

Một món đồ trang sức có hình hai khối cầu bằng nhau giao nhau như hình bên dưới. Khối cầu có bán kính \(25cm\), khoảng cách giữa tâm của hai khối cầu là \(40cm\). Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó, giá mạ vàng \(1{m^2}\) là \(4.700.000\)đồng. Biết diện tích chỏm cầu được tính bởi công thức \(S = 2\pi Rh\) với \(R\) là bán kính khối cầu và \(h\) là chiều cao của chỏm cầu. Số tiền cần dùng để mạ vàng khối trang sức đó gần nhất với giá trị nào sau đây?C:\Users\Admin\Downloads\178065400_151829506943210_5135329336041617126_n.jpg

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Một món đồ trang sức có hình hai khối cầu bằng nhau giao nhau như hình bên dưới. Khối cầu có bán kính \(25cm\), khoảng cách giữa tâm của hai khối cầu là \(40cm\). Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó, giá mạ vàng \(1{m^2}\) là \(4.700.000\)đồng. Biết diện tích chỏm cầu được tính bởi công thức \(S = 2\pi Rh\) với \(R\) là bán kính khối cầu và … [Đọc thêm...] vềMột món đồ trang sức có hình hai khối cầu bằng nhau giao nhau như hình bên dưới. Khối cầu có bán kính \(25cm\), khoảng cách giữa tâm của hai khối cầu là \(40cm\). Nhà sản xuất muốn mạ vàng xung quanh món đồ trang sức đó, giá mạ vàng \(1{m^2}\) là \(4.700.000\)đồng. Biết diện tích chỏm cầu được tính bởi công thức \(S = 2\pi Rh\) với \(R\) là bán kính khối cầu và \(h\) là chiều cao của chỏm cầu. Số tiền cần dùng để mạ vàng khối trang sức đó gần nhất với giá trị nào sau đây?C:\Users\Admin\Downloads\178065400_151829506943210_5135329336041617126_n.jpg

Cho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây? A. \(1,03{{\rm{m}}^{\rm{3}}}\). B. \(0,43{{\rm{m}}^{\rm{3}}}\). C. … [Đọc thêm...] vềCho một cổ vật hình trụ có chiều cao đo được là \(81{\rm{cm}}\), do bị hư hại nên khi tiến hành đo đạc lại thu được \(AB = 50{\rm{cm}},BC = 70{\rm{cm}},CA = 80{\rm{cm}}\), với \(A,B,C\)thuộc đường tròn nắp trên như hình vẽ. Thể tích khối cổ vật ban đầu gần nhất với số nào sau đây?

(Sở Bạc Liêu 2022) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của đường tròn đáy cốc nướ

C. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nốn nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số của lượng nước còn lại trong cốc và lượng nước ban đầu.

Shape Description automatically generated

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (Sở Bạc Liêu 2022) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của đường tròn đáy cốc nướ C. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nốn nằm trên mặt cầu (như hình vẽ) thì thấy … [Đọc thêm...] về

(Sở Bạc Liêu 2022) Trên bàn có một cốc nước hình trụ chứa đầy nước, có chiều cao bằng 3 lần đường kính của đáy; một viên bi và một khối nón đều bằng thủy tinh. Biết viên bi là một khối cầu có đường kính bằng đường kính của đường tròn đáy cốc nướ

C. Người ta từ từ thả vào cốc nước viên bi và khối nón sao cho đỉnh khối nốn nằm trên mặt cầu (như hình vẽ) thì thấy nước trong cốc tràn ra ngoài. Tính tỉ số của lượng nước còn lại trong cốc và lượng nước ban đầu.

Shape Description automatically generated

(Sở Hà Tĩnh 2022) Cho lăng trụ \(ABCD \cdot A\prime B\prime C\prime D\) có đáy là hình chữ nhật với \(AB = \sqrt 6 ,AD = \sqrt 3 ,A\prime C = 3\) và mặt phẳng \(\left( {AA\prime C\prime C} \right)\) vuông góc với mặt đáy. Biêt hai mặt phẳng \(\left( {AA\prime C\prime C} \right)\) và \(\left( {AA\prime B\prime B} \right)\) tạo với nhau góc \(\alpha \) có \(\tan \alpha = \frac{3}{4}\). Thể tích \(V\) của khối lăng trụ \(ABCD \cdot A\prime B\prime C\prime D\prime \) là

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Hà Tĩnh 2022) Cho lăng trụ \(ABCD \cdot A\prime B\prime C\prime D\) có đáy là hình chữ nhật với \(AB = \sqrt 6 ,AD = \sqrt 3 ,A\prime C = 3\) và mặt phẳng \(\left( {AA\prime C\prime C} \right)\) vuông góc với mặt đáy. Biêt hai mặt phẳng \(\left( {AA\prime C\prime C} \right)\) và \(\left( {AA\prime B\prime B} \right)\) tạo với nhau góc \(\alpha \) có \(\tan … [Đọc thêm...] về

(Sở Hà Tĩnh 2022) Cho lăng trụ \(ABCD \cdot A\prime B\prime C\prime D\) có đáy là hình chữ nhật với \(AB = \sqrt 6 ,AD = \sqrt 3 ,A\prime C = 3\) và mặt phẳng \(\left( {AA\prime C\prime C} \right)\) vuông góc với mặt đáy. Biêt hai mặt phẳng \(\left( {AA\prime C\prime C} \right)\) và \(\left( {AA\prime B\prime B} \right)\) tạo với nhau góc \(\alpha \) có \(\tan \alpha = \frac{3}{4}\). Thể tích \(V\) của khối lăng trụ \(ABCD \cdot A\prime B\prime C\prime D\prime \) là

(Sở Hà Tĩnh 2022) Cho hình hộp đứng \(ABCD \cdot A\prime B\prime C\prime D\prime \) có cạnh \(AA\prime = 2\), đáy \(ABCD\) là hình thoi với \(ABC\) là tam giác đều cạnh bằng 4. Gọi \(M,N,P\) lần lượt là trung điểm của \(B\prime C\prime ,C\prime D\prime ,DD\prime \) và \(Q\) thuộc cạnh \(BC\) sao cho \(QC = 3QB\). Thể tích của khối tứ diện \(MNPQ\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Hà Tĩnh 2022) Cho hình hộp đứng \(ABCD \cdot A\prime B\prime C\prime D\prime \) có cạnh \(AA\prime = 2\), đáy \(ABCD\) là hình thoi với \(ABC\) là tam giác đều cạnh bằng 4. Gọi \(M,N,P\) lần lượt là trung điểm của \(B\prime C\prime ,C\prime D\prime ,DD\prime \) và \(Q\) thuộc cạnh \(BC\) sao cho \(QC = 3QB\). Thể tích của khối tứ diện \(MNPQ\) bằng A. … [Đọc thêm...] về

(Sở Hà Tĩnh 2022) Cho hình hộp đứng \(ABCD \cdot A\prime B\prime C\prime D\prime \) có cạnh \(AA\prime = 2\), đáy \(ABCD\) là hình thoi với \(ABC\) là tam giác đều cạnh bằng 4. Gọi \(M,N,P\) lần lượt là trung điểm của \(B\prime C\prime ,C\prime D\prime ,DD\prime \) và \(Q\) thuộc cạnh \(BC\) sao cho \(QC = 3QB\). Thể tích của khối tứ diện \(MNPQ\) bằng

(THPT Lê Thánh Tông – HCM-2022) Hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left[ { – 4;4} \right],\) có các điểm cực trị trên \(\left( { – 4;4} \right)\) là \( – 3; – \frac{4}{3};0;2\) và có đồ thị như hình vẽ. Đặt \(g\left( x \right) = f\left( {{x^3} + 3x} \right) + m\) với \(m\) là tham số. Gọi \({m_1}\) là giá trị của \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = 2022,\) \({m_2}\) là giá trị của \(m\) để \(\mathop {\min }\limits_{\left[ { – 1;0} \right]} g\left( x \right) = 2004.\) Giá trị của \({m_1} – {m_2}\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm VDC Hàm số Tag với:,

Câu hỏi: (THPT Lê Thánh Tông - HCM-2022) Hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left[ { - 4;4} \right],\) có các điểm cực trị trên \(\left( { - 4;4} \right)\) là \( - 3; - \frac{4}{3};0;2\) và có đồ thị như hình vẽ. Đặt \(g\left( x \right) = f\left( {{x^3} + 3x} \right) + m\) với \(m\) là tham số. Gọi \({m_1}\) là giá trị của \(m\) để \(\mathop {\max … [Đọc thêm...] về

(THPT Lê Thánh Tông – HCM-2022) Hàm số \(y = f\left( x \right)\) có đạo hàm trên \(\left[ { – 4;4} \right],\) có các điểm cực trị trên \(\left( { – 4;4} \right)\) là \( – 3; – \frac{4}{3};0;2\) và có đồ thị như hình vẽ. Đặt \(g\left( x \right) = f\left( {{x^3} + 3x} \right) + m\) với \(m\) là tham số. Gọi \({m_1}\) là giá trị của \(m\) để \(\mathop {\max }\limits_{\left[ {0;1} \right]} g\left( x \right) = 2022,\) \({m_2}\) là giá trị của \(m\) để \(\mathop {\min }\limits_{\left[ { – 1;0} \right]} g\left( x \right) = 2004.\) Giá trị của \({m_1} – {m_2}\) bằng

(Sở Hà Tĩnh 2022) Cho hàm số \(y = f\left( x \right)\) là hàm số đa thức bậc bốn và có bảng biến thiên như hình bên. Tìm số điểm cực trị của hàm số \(g\left( x \right) = {2^{ – \frac{1}{{{x^4}}}}}{\left[ {f\left( {2x + 1} \right)} \right]^3}\)

Ngày Thuộc chủ đề:Trắc nghiệm VDC Hàm số Tag với:,

Câu hỏi: (Sở Hà Tĩnh 2022) Cho hàm số \(y = f\left( x \right)\) là hàm số đa thức bậc bốn và có bảng biến thiên như hình bên. Tìm số điểm cực trị của hàm số \(g\left( x \right) = {2^{ - \frac{1}{{{x^4}}}}}{\left[ {f\left( {2x + 1} \right)} \right]^3}\) A. \(7\). B. \(5\). C. \(4\). D. \(6\). Lời giải: Chọn C Ta có: \(g'\left( x \right) = … [Đọc thêm...] về

(Sở Hà Tĩnh 2022) Cho hàm số \(y = f\left( x \right)\) là hàm số đa thức bậc bốn và có bảng biến thiên như hình bên. Tìm số điểm cực trị của hàm số \(g\left( x \right) = {2^{ – \frac{1}{{{x^4}}}}}{\left[ {f\left( {2x + 1} \right)} \right]^3}\)

(THPT Bùi Thị Xuân – Huế – 2022) Cho hàm số \(y = f(x)\) là hàm số bậc ba và có đồ thị \(y = f(2 – x)\) như hình vẽ.

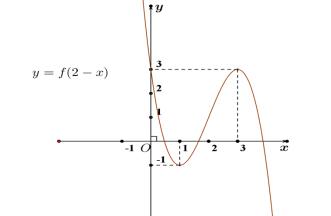
Hỏi phương trình \(\left| {f\left( {\left| {{x^2} – 2x} \right|} \right)} \right| = 1\) có tất cả bao nhiêu nghiệm?

Ngày Thuộc chủ đề:Trắc nghiệm VDC Hàm số Tag với:,

Câu hỏi: (THPT Bùi Thị Xuân – Huế - 2022) Cho hàm số \(y = f(x)\) là hàm số bậc ba và có đồ thị \(y = f(2 - x)\) như hình vẽ. Hỏi phương trình \(\left| {f\left( {\left| {{x^2} - 2x} \right|} \right)} \right| = 1\) có tất cả bao nhiêu nghiệm? A. 8. B. 7. C. 9. D. 6. Lời giải: \(f(2 - x) = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2 - x = … [Đọc thêm...] về

(THPT Bùi Thị Xuân – Huế – 2022) Cho hàm số \(y = f(x)\) là hàm số bậc ba và có đồ thị \(y = f(2 – x)\) như hình vẽ.

Hỏi phương trình \(\left| {f\left( {\left| {{x^2} – 2x} \right|} \right)} \right| = 1\) có tất cả bao nhiêu nghiệm?

(Sở Vĩnh Phúc 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f’\left( x \right)\) như sau

A picture containing diagram Description automatically generated

Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 2\left| x \right| – 4} \right)\) là

Ngày Thuộc chủ đề:Trắc nghiệm VDC Hàm số Tag với:,

Câu hỏi: (Sở Vĩnh Phúc 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f'\left( x \right)\) như sau Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 2\left| x \right| - 4} \right)\) là A. \(2\). B. \(3\). C. \(5\). D. \(10\). Lời giải: Chọn B Dựa vào bảng xét dấu \(f'\left( x … [Đọc thêm...] về

(Sở Vĩnh Phúc 2022) Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng xét dấu \(f’\left( x \right)\) như sau

A picture containing diagram Description automatically generated

Số điểm cực trị của hàm số \(g\left( x \right) = f\left( {{x^3} + 2\left| x \right| – 4} \right)\) là