ĐỀ BÀI Xét một bảng ô vuông gồm $4\times 4$ ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số $1$ hoặc $-1$ sao cho tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng $0$. Hỏi có bao nhiêu cách?90 Nhận xét 1: Trên mỗi hàng có $2$ số $1$ và $2$ số $-1$, mỗi cột có $2$ số $1$ và $2$ số $-1$ Nhận xét 2: Để tổng các số trong mỗi hàng và trong mỗi cột bằng … [Đọc thêm...] vềXét một bảng ô vuông gồm $4\times 4$ ô vuông. Người ta điền vào mỗi ô vuông đó một trong hai số $1$ hoặc $-1$ sao cho tổng các số trong mỗi hàng và tổng các số trong mỗi cột đều bằng $0$. Hỏi có bao nhiêu cách?90 Nhận xét 1: Trên mỗi hàng có $2$ số $1$ và $2$ số $-1$, mỗi cột có $2$ số $1$ và $2$ số $-1$ Nhận xét 2: Để tổng các số trong mỗi hàng và trong mỗi cột bằng $0$ đồng thời có không quá hai số bằng nhau và ba hàng đầu tiên đã được xếp số thì ta chỉ có một cách xếp hàng thứ tư.Do vậy ta tìm số cách xếp ba hàng đầu tiên. Phương pháp giải bài này là xếp theo hàng. Các hàng được đánh số như sau:
Kết quả tìm kiếm cho: dơ số 4 và số 2
[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { – 3} \right) = f\left( {\frac{3}{2}} \right) = – \frac{{19}}{4}\) và đồ thị hàm số \(y = f’\left( x \right)\) có dạng như hình vẽ.
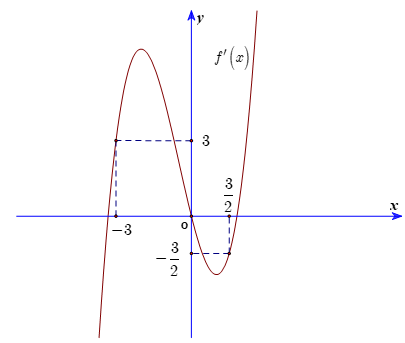
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( x \right)\) trên \(\left[ { – 2;\frac{3}{2}} \right]\) là
[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { - 3} \right) = f\left( {\frac{3}{2}} \right) = - \frac{{19}}{4}\) và đồ thị hàm số \(y = f'\left( x \right)\) có dạng như hình vẽ. Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( … [Đọc thêm...] về[Mức độ 4] Cho hàm số đa thức \(y = f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\). Biết rằng \(f\left( 0 \right) = 0\), \(f\left( { – 3} \right) = f\left( {\frac{3}{2}} \right) = – \frac{{19}}{4}\) và đồ thị hàm số \(y = f’\left( x \right)\) có dạng như hình vẽ.
Hàm số \(g\left( x \right) = \left| {4f\left( x \right) + 2{x^2}} \right|\) giá trị lớn nhất của \(g\left( x \right)\) trên \(\left[ { – 2;\frac{3}{2}} \right]\) là
[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { – 6} \right) = 42\) và bảng xét dấu đạo hàm như

Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { – \,3{x^4}\,\, + \,\,12{x^2}\, – \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, – 48{x^2}\) trên đoạn \(\left[ { – 1;1} \right]\) bằng
[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { - 6} \right) = 42\) và bảng xét dấu đạo hàm như Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { - \,3{x^4}\,\, + \,\,12{x^2}\, - \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, - 48{x^2}\) trên đoạn \(\left[ { - 1;1} \right]\) bằng A. 3. B. 0. C. 1. D. 2. Lời … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(y\, = \,f(x)\,\) có đạo hàm và liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( { – 6} \right) = 42\) và bảng xét dấu đạo hàm như
Giá trị nhỏ nhất của hàm số \(y\, = \,f\left( { – \,3{x^4}\,\, + \,\,12{x^2}\, – \,15} \right)\, + \,2{x^6}\, + \,6{x^4}\, – 48{x^2}\) trên đoạn \(\left[ { – 1;1} \right]\) bằng
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
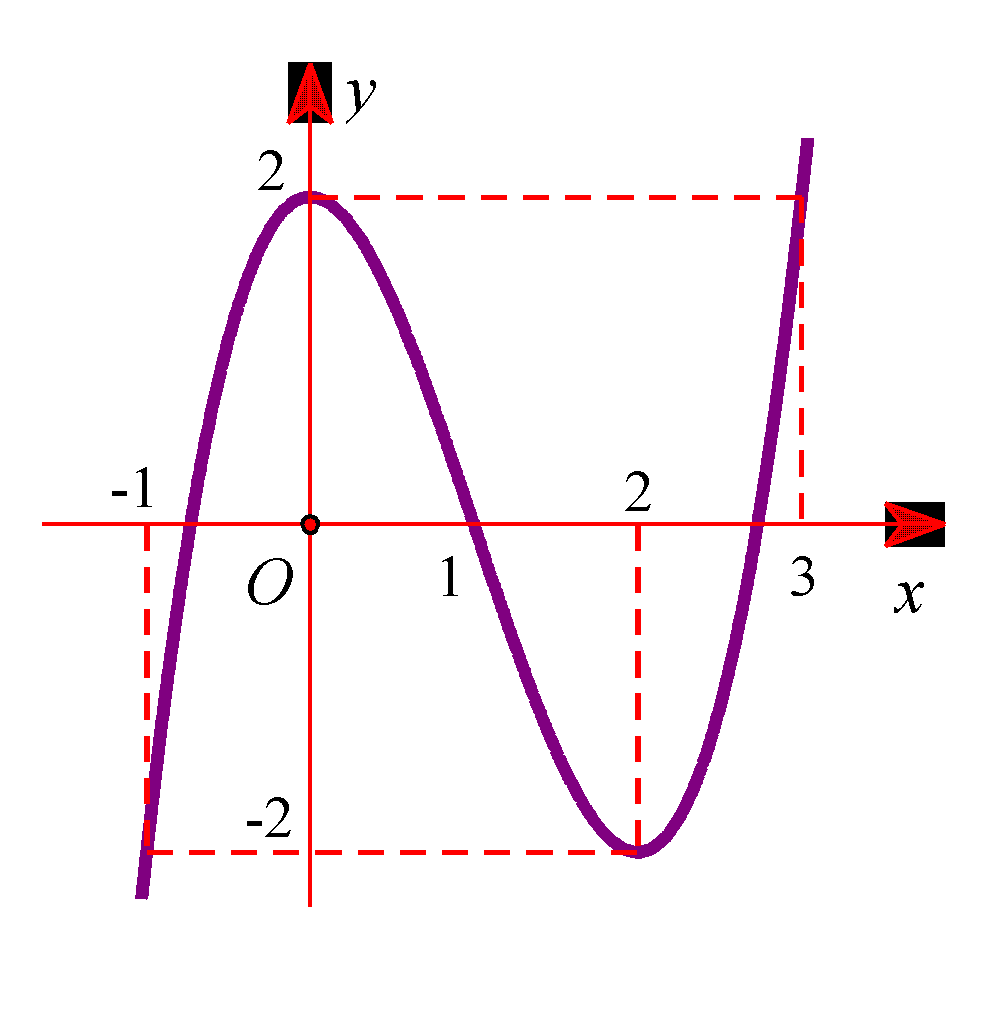
[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x - m} \right) - \frac{1}{2}{\left( {x - m - 1} \right)^2} + 2022\), với \(m\) là tham số thự C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng … [Đọc thêm...] về[ Mức độ 4] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và có đồ thị
\(y = f’\left( x \right)\) như hình vẽ bên. Đặt \(g\left( x \right) = f\left( {x – m} \right) – \frac{1}{2}{\left( {x – m – 1} \right)^2} + 2022\), với \(m\) là tham số thự
C. Gọi \(S\) là tập hợp các giá trị nguyên dương của \(m\) để hàm số \(y = g\left( x \right)\) đồng biến trên khoảng \(\left( {2;3} \right)\). Tổng tất cả các phần tử trong \(S\) bằng
[ Mức độ 4] Cho hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) có đạo hàm trên \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\)và \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\). Đồ thị hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) như hình bên. Có bao nhiêu số nguyên dương \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) để hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) nghịch biến trên \(12\)?

[ Mức độ 4] Cho hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\) có đạo hàm trên \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\)và \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\). Đồ thị hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x - \frac{a}{4}} \right|\) như hình bên. Có bao … [Đọc thêm...] về[ Mức độ 4] Cho hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) có đạo hàm trên \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\)và \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\). Đồ thị hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) như hình bên. Có bao nhiêu số nguyên dương \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) để hàm số \(y = \left| {4f\left( {\sin x} \right) + \cos 2x – \frac{a}{4}} \right|\) nghịch biến trên \(12\)?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có \(f\left( 5 \right) > 8\) và \(f\left( 1 \right) = 0.\) Biết hàm số
\(y = f’\left( x \right)\) có đồ thị như hình vẽ bên.
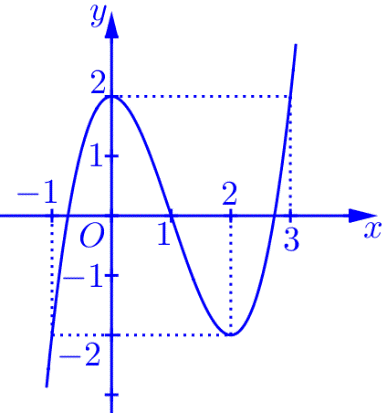
Hàm số \(g\left( x \right) = \left| {f\left( {1 – \frac{x}{2}} \right) – \frac{{{x^2}}}{8}} \right|\) nghịch biến trên khoảng nào dưới đây?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có \(f\left( 5 \right) > 8\) và \(f\left( 1 \right) = 0.\) Biết hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(g\left( x \right) = \left| {f\left( {1 - \frac{x}{2}} \right) - \frac{{{x^2}}}{8}} \right|\) nghịch biến trên khoảng nào dưới đây? A. \(\left( { - 8; - 4} \right)\). B. … [Đọc thêm...] về[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có \(f\left( 5 \right) > 8\) và \(f\left( 1 \right) = 0.\) Biết hàm số
\(y = f’\left( x \right)\) có đồ thị như hình vẽ bên.
Hàm số \(g\left( x \right) = \left| {f\left( {1 – \frac{x}{2}} \right) – \frac{{{x^2}}}{8}} \right|\) nghịch biến trên khoảng nào dưới đây?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ sau.
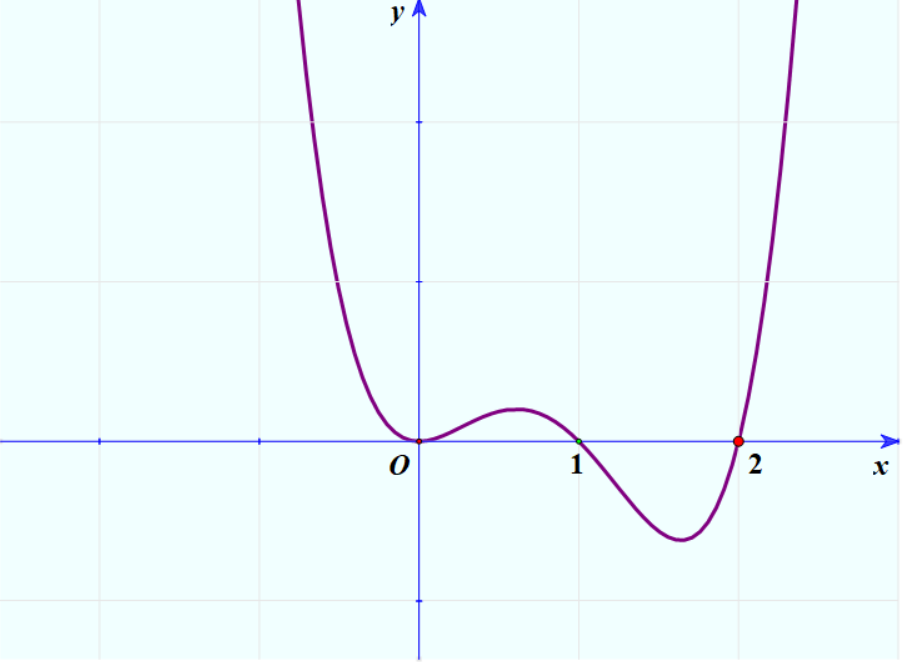
Hỏi đồ thị hàm số \(y = \frac{{{f^2}\left( x \right)\sqrt {{x^2} + x} }}{{\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]\left( {2{x^5} + {x^4} – 10{x^3} – 5{x^2} + 8x + 4} \right)}}\) có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ sau. Hỏi đồ thị hàm số \(y = \frac{{{f^2}\left( x \right)\sqrt {{x^2} + x} }}{{\left[ {{f^2}\left( x \right) - 2f\left( x \right)} \right]\left( {2{x^5} + {x^4} - 10{x^3} - 5{x^2} + 8x + 4} \right)}}\) có bao nhiêu đường tiệm cận đứng và tiệm cận ngang? A. \(7\). B. \(6\). C. … [Đọc thêm...] về[ Mức độ 4] Cho hàm số bậc bốn \(y = f\left( x \right)\) có đồ thị như hình vẽ sau.
Hỏi đồ thị hàm số \(y = \frac{{{f^2}\left( x \right)\sqrt {{x^2} + x} }}{{\left[ {{f^2}\left( x \right) – 2f\left( x \right)} \right]\left( {2{x^5} + {x^4} – 10{x^3} – 5{x^2} + 8x + 4} \right)}}\) có bao nhiêu đường tiệm cận đứng và tiệm cận ngang?
[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 5 \right) = 3\) . Hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên dưới:

Số nghiệm thực của phương trình \(f\left( x \right) = 4\) là
[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 5 \right) = 3\) . Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ bên dưới: Số nghiệm thực của phương trình \(f\left( x \right) = 4\) là A. 5 B. 2 C. 3 D. 4 Lời giải: Gọi \({S_1}\) là diện tích hình phẳng giới hạn bởi \(y = f'\left( x \right);y = … [Đọc thêm...] về[Mức độ 3] Cho hàm số \(y = f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và \(f\left( 5 \right) = 3\) . Hàm số \(y = f’\left( x \right)\) có đồ thị như hình vẽ bên dưới:
Số nghiệm thực của phương trình \(f\left( x \right) = 4\) là
Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \(OO’ = 5\)\({\rm{cm}}\), \(OA = 10\)\({\rm{cm}}\), \(OB = 20\) \({\rm{cm}}\), đường cong \(AB\) là một phần của parabol có đỉnh là điểm\(A\). Thể tích của chiếc mũ bằng
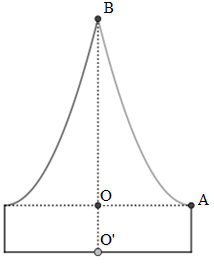
Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \(OO' = 5\)\({\rm{cm}}\), \(OA = 10\)\({\rm{cm}}\), \(OB = 20\) \({\rm{cm}}\), đường cong \(AB\) là một phần của parabol có đỉnh là điểm\(A\). Thể tích của chiếc mũ bằng A. … [Đọc thêm...] vềChuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng \(OO’ = 5\)\({\rm{cm}}\), \(OA = 10\)\({\rm{cm}}\), \(OB = 20\) \({\rm{cm}}\), đường cong \(AB\) là một phần của parabol có đỉnh là điểm\(A\). Thể tích của chiếc mũ bằng
Cho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\)
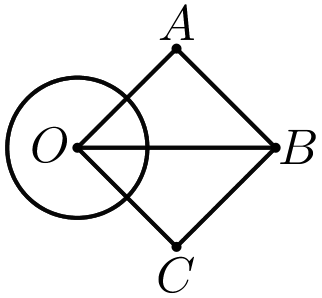
Cho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\) A. \(V = \frac{{8\left( {3 + 4\sqrt 2 } \right)\pi }}{3}.\) B. \(V = \frac{{8\left( {2 + 5\sqrt 2 } \right)\pi }}{3}.\) C. \(V = \frac{{8\left( {3 + … [Đọc thêm...] vềCho hình tròn tâm \(O\) có bán kính \(R = 2\) và hình vuông \(OABC\) có cạnh bằng \(4\) (như hình vẽ bên). Tính thể tích \(V\) của vật thể tròn xoay khi quay mô hình bên xung quanh trục là đường thẳng \(OB.\)