Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: dơ số 4 và số 2

Cho hàm số \(f\left( x \right)\) xác định và có đạo hàm trên \(\mathbb{R}\). Biết hàm số \(g\left( x \right) = f\left( {\ln \left( {\sqrt {{x^2} + 1} – x} \right)} \right)\) có đồ thị như hình bên. Hàm số \(f\left( {\frac{x}{2}} \right)\) đồng biến trên

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Cho hàm số \(f\left( x \right)\) xác định và có đạo hàm trên \(\mathbb{R}\). Biết hàm số \(g\left( x \right) = f\left( {\ln \left( {\sqrt {{x^2} + 1} - x} \right)} \right)\) có đồ thị như hình bên. Hàm số \(f\left( {\frac{x}{2}} \right)\) đồng biến trên A. \(\left( { - \infty ; - 1} \right)\). B. \(\left( {1; + \infty } \right)\). C. \(\left( { - \infty ; … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) xác định và có đạo hàm trên \(\mathbb{R}\). Biết hàm số \(g\left( x \right) = f\left( {\ln \left( {\sqrt {{x^2} + 1} – x} \right)} \right)\) có đồ thị như hình bên. Hàm số \(f\left( {\frac{x}{2}} \right)\) đồng biến trên

Cho hàm số đa thức \(y = f\left( x \right)\) có đồ thị \(y = f’\left( x \right)\) như hình vẽ

do thi

Điều kiện cần và đủ của tham số \(a\) để hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2} – a} \right|\) đồng biến trên khoảng \(\left( { – 2;0} \right)\) và nghịch biến trên khoảng \(\left( {0;4} \right)\) là

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Cho hàm số đa thức \(y = f\left( x \right)\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ Điều kiện cần và đủ của tham số \(a\) để hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2} - a} \right|\) đồng biến trên khoảng \(\left( { - 2;0} \right)\) và nghịch biến trên khoảng \(\left( {0;4} \right)\) là A. \(a \le 4f\left( { - 2} \right) + … [Đọc thêm...] vềCho hàm số đa thức \(y = f\left( x \right)\) có đồ thị \(y = f’\left( x \right)\) như hình vẽ

do thi

Điều kiện cần và đủ của tham số \(a\) để hàm số \(g\left( x \right) = \left| {4f\left( x \right) + {x^2} – a} \right|\) đồng biến trên khoảng \(\left( { – 2;0} \right)\) và nghịch biến trên khoảng \(\left( {0;4} \right)\) là

Cho hàm số bậc bốn \(y = f\left( x \right)\)có \(f\left( { – \frac{3}{2}} \right) < 2\) và \(f\left( 1 \right) = 0\). Biết hàm số \(f’\left( x \right)\) có đồ thị như hình vẽ bên.

C:\Users\admin\Downloads\dt1.jpg

Hàm số \(g\left( x \right) = \left| {f\left( {1 – \frac{x}{2}} \right) – \frac{{{x^2}}}{8}} \right|\) đồng biến trên khoảng nào dưới đây

Ngày Thuộc chủ đề:Trắc nghiệm Tính đơn điệu của hàm số Tag với:,

Câu hỏi: Cho hàm số bậc bốn \(y = f\left( x \right)\)có \(f\left( { - \frac{3}{2}} \right) < 2\) và \(f\left( 1 \right) = 0\). Biết hàm số \(f'\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số \(g\left( x \right) = \left| {f\left( {1 - \frac{x}{2}} \right) - \frac{{{x^2}}}{8}} \right|\) đồng biến trên khoảng nào dưới đây A. \(\left( { - \infty ; - 4} … [Đọc thêm...] vềCho hàm số bậc bốn \(y = f\left( x \right)\)có \(f\left( { – \frac{3}{2}} \right) < 2\) và \(f\left( 1 \right) = 0\). Biết hàm số \(f’\left( x \right)\) có đồ thị như hình vẽ bên.

C:\Users\admin\Downloads\dt1.jpg

Hàm số \(g\left( x \right) = \left| {f\left( {1 – \frac{x}{2}} \right) – \frac{{{x^2}}}{8}} \right|\) đồng biến trên khoảng nào dưới đây

Đề bài: Cá hồi Thái Bình Dương đến mùa sinh sản chúng thường bơi từ biển đến thượng nguồn con sông để đẻ trứng trên sỏi đá rồi chết. Khi nghiên cứu một con cá hồi sinh sản người ta phát hiện ra quy luật nó chuyển động trong nước yên lặng là \(s =  – \frac{{{t^2}}}{{10}} + 4t,\) với t (giờ) là khoảng thời gian tính từ lúc cá bắt đầu chuyển động và s (km) là quảng đường cá bơi được trong khoảng thời gian đó. Nếu thả con cá hồi đó vào một dòng sông có vận tốc dòng nước chảy là 2km/h Tính khoảng cách xa nhất mà con cá hồi đó có thể bơi ngược dòng nước đến nơi đẻ trứng.

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:

Câu hỏi: Cá hồi Thái Bình Dương đến mùa sinh sản chúng thường bơi từ biển đến thượng nguồn con sông để đẻ trứng trên sỏi đá rồi chết. Khi nghiên cứu một con cá hồi sinh sản người ta phát hiện ra quy luật nó chuyển động trong nước yên lặng là \(s =  - \frac{{{t^2}}}{{10}} + 4t,\) với t (giờ) là khoảng thời gian tính từ lúc cá bắt đầu chuyển động và s (km) là quảng đường … [Đọc thêm...] vềĐề bài: Cá hồi Thái Bình Dương đến mùa sinh sản chúng thường bơi từ biển đến thượng nguồn con sông để đẻ trứng trên sỏi đá rồi chết. Khi nghiên cứu một con cá hồi sinh sản người ta phát hiện ra quy luật nó chuyển động trong nước yên lặng là \(s =  – \frac{{{t^2}}}{{10}} + 4t,\) với t (giờ) là khoảng thời gian tính từ lúc cá bắt đầu chuyển động và s (km) là quảng đường cá bơi được trong khoảng thời gian đó. Nếu thả con cá hồi đó vào một dòng sông có vận tốc dòng nước chảy là 2km/h Tính khoảng cách xa nhất mà con cá hồi đó có thể bơi ngược dòng nước đến nơi đẻ trứng.

Đề: Một vi sinh đặc biệt X có cách sinh sản vô tính kì lạ. Tại thời điểm 0h có đúng 2 con, với mỗi con X, sống được tới giờ thứ n (với n là số nguyên dương) thì ngay lập tức tại thời điểm đó nó đẻ một lần ra \({2^n}\) con khác. Tuy nhiên do chu kì của con X ngắn nên ngay sau khi đẻ xong lần thứ 4 nó lập tức chết. Hỏi lúc 6h01 phút có bao nhiêu con sinh vật đang sống? 

Ngày Thuộc chủ đề:Trắc nghiệm Toán thực tế về hàm số mũ và Lôgarit Tag với:

---- Câu hỏi: Một vi sinh đặc biệt X có cách sinh sản vô tính kì lạ. Tại thời điểm 0h có đúng 2 con, với mỗi con X, sống được tới giờ thứ n (với n là số nguyên dương) thì ngay lập tức tại thời điểm đó nó đẻ một lần ra \({2^n}\) con khác. Tuy nhiên do chu kì của con X ngắn nên ngay sau khi đẻ xong lần thứ 4 nó lập tức chết. Hỏi lúc 6h01 phút có bao nhiêu con sinh vật … [Đọc thêm...] vềĐề: Một vi sinh đặc biệt X có cách sinh sản vô tính kì lạ. Tại thời điểm 0h có đúng 2 con, với mỗi con X, sống được tới giờ thứ n (với n là số nguyên dương) thì ngay lập tức tại thời điểm đó nó đẻ một lần ra \({2^n}\) con khác. Tuy nhiên do chu kì của con X ngắn nên ngay sau khi đẻ xong lần thứ 4 nó lập tức chết. Hỏi lúc 6h01 phút có bao nhiêu con sinh vật đang sống? 

Hệ thống định vị toàn cầu GPS (Global Positioning System) là một hệ thống cho phép xác định vị trí của một vật thể trong không gian

Ngày Thuộc chủ đề:_Trắc nghiệm Hình học OXYZ Tag với:

Bài toán: Hệ thống định vị toàn cầu GPS (Global Positioning System) là một hệ thống cho phép xác định vị trí của một vật thể trong không gian. Trong cùng một thời điểm vị trí của một điểm $M$ trong không gian sẽ được xác định bởi bốn vệ tinh cho trước nhờ các bộ thu phát tín hiệu đặt trên các vệ tinh. Giả sử trong không gian $Oxyz$, tỉ lệ dài trên các trục là 10 km tính cho một … [Đọc thêm...] vềHệ thống định vị toàn cầu GPS (Global Positioning System) là một hệ thống cho phép xác định vị trí của một vật thể trong không gian

Cho đường tròn tâm $O$, bán kính bằng 2 . Trên đường tròn, lấy 6 điểm chia đều đường tròn, lần lượt là $A,B,C,D,E,F$.

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:

Bài toán Cho đường tròn tâm $O$, bán kính bằng 2 . Trên đường tròn, lấy 6 điểm chia đều đường tròn, lần lượt là $A,B,C,D,E,F$. Vẽ cung tròn $C_{1}$ tiếp xúc với hai đoạn thẳng $OA$ và $OB$, đi qua hai điểm $A$ và $B$. Tương tự, vẽ cung tròn $C_{2}$ tiếp xúc với hai đoạn thẳng $OB$ và $OC$, đi qua hai điểm $B$ và $C$. Tiếp tục bằng cách tương tự, ta vẽ các cung tròn … [Đọc thêm...] vềCho đường tròn tâm $O$, bán kính bằng 2 . Trên đường tròn, lấy 6 điểm chia đều đường tròn, lần lượt là $A,B,C,D,E,F$.

Một bức tường hình chữ nhật $ABCD$ có kích thước $6\left(m\right),4\left(m\right)$ được bạn Hà trang trí bằng cách vẽ hai đồ thị $f\left(x\right)=a^{x},g\left(x\right)=\mathrm{\,lo}\mathrm{\,g}_{b}x$ đối xứng nhau qua đường thẳng $d:y=x$ và chia thành ba phần

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:

Bài toán: Một bức tường hình chữ nhật $ABCD$ có kích thước $6\left(m\right),4\left(m\right)$ được bạn Hà trang trí bằng cách vẽ hai đồ thị $f\left(x\right)=a^{x},g\left(x\right)=\mathrm{\,lo}\mathrm{\,g}_{b}x$ đối xứng nhau qua đường thẳng $d:y=x$ và chia thành ba phần (tham khảo hình vẽ bên). Phần $H_{1}$ được sơn màu xanh da trời, phần $H_{2}$ được sơn màu vàng, phần $H_{3}$ … [Đọc thêm...] vềMột bức tường hình chữ nhật $ABCD$ có kích thước $6\left(m\right),4\left(m\right)$ được bạn Hà trang trí bằng cách vẽ hai đồ thị $f\left(x\right)=a^{x},g\left(x\right)=\mathrm{\,lo}\mathrm{\,g}_{b}x$ đối xứng nhau qua đường thẳng $d:y=x$ và chia thành ba phần

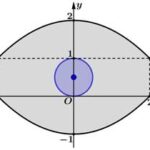
Bạn An thực hiện thiết kế một logo hình con mắt cho một phòng khám nhãn khoa. Logo là một hình phẳng giới hạn bởi hai parabol $y=f\left(x\right)$ và $y=g\left(x\right)$ có các kích thước như hình vẽ dưới đây

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:

Bài toán: Bạn An thực hiện thiết kế một logo hình con mắt cho một phòng khám nhãn khoa. Logo là một hình phẳng giới hạn bởi hai parabol $y=f\left(x\right)$ và $y=g\left(x\right)$ có các kích thước như hình vẽ dưới đây (phần được tô màu đen) và một hình tròn có bán kính bằng $0,5\mathrm{\,dm}$ ở giữa là phần con ngươi (phần được tô màu xanh), đơn vị trên mỗi trục tọa độ là … [Đọc thêm...] vềBạn An thực hiện thiết kế một logo hình con mắt cho một phòng khám nhãn khoa. Logo là một hình phẳng giới hạn bởi hai parabol $y=f\left(x\right)$ và $y=g\left(x\right)$ có các kích thước như hình vẽ dưới đây