Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: 0a

Người ta phân khu vườn hình chữ nhật \(ABCD\), \(AB = 10{\rm{m}}\), \(AD = 20{\rm{m}}\)thành năm khu vực bởi bốn parabol rồi trồng hoa ở khu vực trung tâm như hình vẽ kèm theo. Trong đó:➀ Hai parabol kề nhau tiếp xúc nhau tại một trong các điểm \(A,\,B,\,C,\,D\).➁ Khu vực trồng hoa là một hình có hai trục đối xứng.Với việc làm như đã nêu thì diện tích của khu vực trồng hoa có thể đạt giá trị lớn nhất là bao nhiêu?

Ngày Thuộc chủ đề:Trắc nghiệm Ứng dụng Tích phân Tag với:,

Câu hỏi: Người ta phân khu vườn hình chữ nhật \(ABCD\), \(AB = 10{\rm{m}}\), \(AD = 20{\rm{m}}\)thành năm khu vực bởi bốn parabol rồi trồng hoa ở khu vực trung tâm như hình vẽ kèm theo. Trong đó:➀ Hai parabol kề nhau tiếp xúc nhau tại một trong các điểm \(A,\,B,\,C,\,D\).➁ Khu vực trồng hoa là một hình có hai trục đối xứng.Với việc làm như đã nêu thì diện tích của khu vực … [Đọc thêm...] vềNgười ta phân khu vườn hình chữ nhật \(ABCD\), \(AB = 10{\rm{m}}\), \(AD = 20{\rm{m}}\)thành năm khu vực bởi bốn parabol rồi trồng hoa ở khu vực trung tâm như hình vẽ kèm theo. Trong đó:➀ Hai parabol kề nhau tiếp xúc nhau tại một trong các điểm \(A,\,B,\,C,\,D\).➁ Khu vực trồng hoa là một hình có hai trục đối xứng.Với việc làm như đã nêu thì diện tích của khu vực trồng hoa có thể đạt giá trị lớn nhất là bao nhiêu?

Cho hình nón chứa năm mặt cầu cùng có bán kính là 1, trong đó bốn mặt cầu tiếp xúc với đáy, tiếp xúc đôi một với nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ năm tiếp xúc với bốn mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy hình nón.

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:,

Câu hỏi: Cho hình nón chứa năm mặt cầu cùng có bán kính là 1, trong đó bốn mặt cầu tiếp xúc với đáy, tiếp xúc đôi một với nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ năm tiếp xúc với bốn mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy hình nón. A. \(2\sqrt 3 + 1\). B. \(2\sqrt 2 + 1\). C. \(2\sqrt 2 - 1\). D. \(3\sqrt 2 + … [Đọc thêm...] vềCho hình nón chứa năm mặt cầu cùng có bán kính là 1, trong đó bốn mặt cầu tiếp xúc với đáy, tiếp xúc đôi một với nhau và tiếp xúc với mặt xung quanh của hình nón. Mặt cầu thứ năm tiếp xúc với bốn mặt cầu kia và tiếp xúc với mặt xung quanh của hình nón. Tính bán kính đáy hình nón.

Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm \(A,B\)sao cho cung \(AB\)có số đo bằng \({120^ \circ }\). Người ta cắt khúc gỗ bởi một mặt phẳng đi qua \(A,B\)và tâm của hình trụ (tâm của hình trụ là trung điềm của đoạn nối tâm 2 đáy) để được thiết diện như hình vẽ.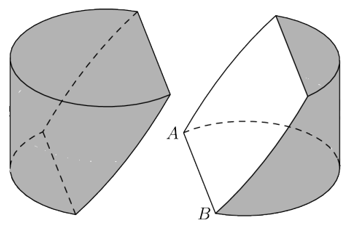Biết diện tích \(S\)của thiết diện thu được có dạng\(S = a\pi + b\sqrt 3 \) . Tính \(P = a + b\)

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Một khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm \(A,B\)sao cho cung \(AB\)có số đo bằng \({120^ \circ }\). Người ta cắt khúc gỗ bởi một mặt phẳng đi qua \(A,B\)và tâm của hình trụ (tâm của hình trụ là trung điềm của đoạn nối tâm 2 đáy) để được thiết diện như hình vẽ.Biết diện tích \(S\)của thiết diện … [Đọc thêm...] vềMột khối gỗ hình trụ với bán kính đáy bằng 6 và chiều cao bằng 8. Trên một đường tròn đáy nào đó ta lấy hai điểm \(A,B\)sao cho cung \(AB\)có số đo bằng \({120^ \circ }\). Người ta cắt khúc gỗ bởi một mặt phẳng đi qua \(A,B\)và tâm của hình trụ (tâm của hình trụ là trung điềm của đoạn nối tâm 2 đáy) để được thiết diện như hình vẽ.Biết diện tích \(S\)của thiết diện thu được có dạng\(S = a\pi + b\sqrt 3 \) . Tính \(P = a + b\)

(Đại học Hồng Đức – 2022) Cho hình nón đỉnh \(S\) có độ dài đường cao là \(R\) và đáy là đường tròn tâm \(O\) bán kính \(R\). Gọi \((d)\) là tiếp tuyến của đường tròn đáy tại \(A\) và \((P)\) là mặt phẳng chứa \(SA\) và \((d)\). Mặt phẳng \((Q)\) thay đổi qua \(S\) cắt đường tròn \(O\) tại hai điểm \(C,D\) sao cho \(CD = \sqrt 3 R\). Gọi \(\alpha \) là góc tạo bởi \((P)\) và \((Q)\). Tính giá trị lớn nhất của \(\cos \alpha \).

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (Đại học Hồng Đức – 2022) Cho hình nón đỉnh \(S\) có độ dài đường cao là \(R\) và đáy là đường tròn tâm \(O\) bán kính \(R\). Gọi \((d)\) là tiếp tuyến của đường tròn đáy tại \(A\) và \((P)\) là mặt phẳng chứa \(SA\) và \((d)\). Mặt phẳng \((Q)\) thay đổi qua \(S\) cắt đường tròn \(O\) tại hai điểm \(C,D\) sao cho \(CD = \sqrt 3 R\). Gọi \(\alpha \) là góc tạo bởi … [Đọc thêm...] về

(Đại học Hồng Đức – 2022) Cho hình nón đỉnh \(S\) có độ dài đường cao là \(R\) và đáy là đường tròn tâm \(O\) bán kính \(R\). Gọi \((d)\) là tiếp tuyến của đường tròn đáy tại \(A\) và \((P)\) là mặt phẳng chứa \(SA\) và \((d)\). Mặt phẳng \((Q)\) thay đổi qua \(S\) cắt đường tròn \(O\) tại hai điểm \(C,D\) sao cho \(CD = \sqrt 3 R\). Gọi \(\alpha \) là góc tạo bởi \((P)\) và \((Q)\). Tính giá trị lớn nhất của \(\cos \alpha \).

(THPT Nho Quan A – Ninh Bình – 2022) Cho hình nón đỉnh \(S\) có đường cao \(h = a\sqrt 3 \). Một mặt phẳng \((\alpha )\) đi qua đỉnh \(S\), cắt đường tròn đáy tại hai điểm \(A,B\) sao cho \(AB = 8a\) và tạo với mặt đáy một góc \(30^\circ \). Tính diện tích xung quanh của hình nón.

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (THPT Nho Quan A – Ninh Bình – 2022) Cho hình nón đỉnh \(S\) có đường cao \(h = a\sqrt 3 \). Một mặt phẳng \((\alpha )\) đi qua đỉnh \(S\), cắt đường tròn đáy tại hai điểm \(A,B\) sao cho \(AB = 8a\) và tạo với mặt đáy một góc \(30^\circ \). Tính diện tích xung quanh của hình nón. A. \(\frac{{10\sqrt 7 \pi }}{3}{a^2}\). B. \(20\sqrt 7 \pi {a^2}\). C. … [Đọc thêm...] về

(THPT Nho Quan A – Ninh Bình – 2022) Cho hình nón đỉnh \(S\) có đường cao \(h = a\sqrt 3 \). Một mặt phẳng \((\alpha )\) đi qua đỉnh \(S\), cắt đường tròn đáy tại hai điểm \(A,B\) sao cho \(AB = 8a\) và tạo với mặt đáy một góc \(30^\circ \). Tính diện tích xung quanh của hình nón.

(Sở Ninh Bình 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, có thể tích là \(V\). Gọi \(M\) là trung điểm của cạnh \(SA,N\) là điểm trên cạnh \(SB\) sao cho \(SN = 3NB\). Mặt phẳng \((P)\) thay đổi đi qua các điểm \(M,N\) và cắt các cạnh \(SC,SD\) lần lượt tại hai điểm phân biệt \(P,Q\). Tìm giá trị lớn nhất của thể tích khối chóp \(S.MNPQ\).

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Ninh Bình 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, có thể tích là \(V\). Gọi \(M\) là trung điểm của cạnh \(SA,N\) là điểm trên cạnh \(SB\) sao cho \(SN = 3NB\). Mặt phẳng \((P)\) thay đổi đi qua các điểm \(M,N\) và cắt các cạnh \(SC,SD\) lần lượt tại hai điểm phân biệt \(P,Q\). Tìm giá trị lớn nhất của thể tích khối chóp … [Đọc thêm...] về

(Sở Ninh Bình 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành, có thể tích là \(V\). Gọi \(M\) là trung điểm của cạnh \(SA,N\) là điểm trên cạnh \(SB\) sao cho \(SN = 3NB\). Mặt phẳng \((P)\) thay đổi đi qua các điểm \(M,N\) và cắt các cạnh \(SC,SD\) lần lượt tại hai điểm phân biệt \(P,Q\). Tìm giá trị lớn nhất của thể tích khối chóp \(S.MNPQ\).

(Sở Thái Nguyên 2022) Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = 6\sqrt 3 ,\widehat {CAB} = 30^\circ \). Đỉnh \(S\) cách đều ba điểm \(A,B,C\) và cạnh bên \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \(45^\circ \). Hai điểm \(M,Q\) lần lượt thuộc các đoạn \(AB\) và \(SB\) sao cho \(AM = 2MB,QB = 2QS\). Mặt phẳng \(\left( \alpha \right)\) chứa \(M,Q\) và song song với đường thẳng \(BC\) chia khối chóp \(S.ABC\) thành hai khối đa diện có thể tích lần lượt là \({V_1},{V_2}\left( {{V_1} < {V_2}} \right)\). Giá trị của \({V_2}\) là

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Thái Nguyên 2022) Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = 6\sqrt 3 ,\widehat {CAB} = 30^\circ \). Đỉnh \(S\) cách đều ba điểm \(A,B,C\) và cạnh bên \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \(45^\circ \). Hai điểm \(M,Q\) lần lượt thuộc các đoạn \(AB\) và \(SB\) sao cho \(AM = 2MB,QB = 2QS\). Mặt phẳng … [Đọc thêm...] về

(Sở Thái Nguyên 2022) Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(B\), \(AB = 6\sqrt 3 ,\widehat {CAB} = 30^\circ \). Đỉnh \(S\) cách đều ba điểm \(A,B,C\) và cạnh bên \(SB\) tạo với mặt phẳng \(\left( {ABC} \right)\) một góc \(45^\circ \). Hai điểm \(M,Q\) lần lượt thuộc các đoạn \(AB\) và \(SB\) sao cho \(AM = 2MB,QB = 2QS\). Mặt phẳng \(\left( \alpha \right)\) chứa \(M,Q\) và song song với đường thẳng \(BC\) chia khối chóp \(S.ABC\) thành hai khối đa diện có thể tích lần lượt là \({V_1},{V_2}\left( {{V_1} < {V_2}} \right)\). Giá trị của \({V_2}\) là

(Sở Phú Thọ 2022) Cho hình nón \(\left( \aleph \right)\) có chiều cao bằng \(2a\). Cắt \(\left( \aleph \right)\) bởi một mặt phẳng đi qua đỉnh và cách tâm của đáy một khoảng bằng \(a\) ta được thiết diện có diện tích bằng \(\frac{{4{a^2}\sqrt {11} }}{3}\). Thể tích của khối nón đã cho bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khối tròn xoay Tag với:, ,

Câu hỏi: (Sở Phú Thọ 2022) Cho hình nón \(\left( \aleph \right)\) có chiều cao bằng \(2a\). Cắt \(\left( \aleph \right)\) bởi một mặt phẳng đi qua đỉnh và cách tâm của đáy một khoảng bằng \(a\) ta được thiết diện có diện tích bằng \(\frac{{4{a^2}\sqrt {11} }}{3}\). Thể tích của khối nón đã cho bằng A. \(\frac{{10{\rm{\pi }}{a^3}}}{3}\). B. \(10{\rm{\pi … [Đọc thêm...] về

(Sở Phú Thọ 2022) Cho hình nón \(\left( \aleph \right)\) có chiều cao bằng \(2a\). Cắt \(\left( \aleph \right)\) bởi một mặt phẳng đi qua đỉnh và cách tâm của đáy một khoảng bằng \(a\) ta được thiết diện có diện tích bằng \(\frac{{4{a^2}\sqrt {11} }}{3}\). Thể tích của khối nón đã cho bằng

(Sở Bạc Liêu 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(AB = 1\), cạnh bên \(SA = 1\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Kí hiệu \(M\) là điểm di động trên đoạn \(CD\) và \(N\) là điểm di động trên đoạn \(CB\) và góc \(\widehat {MAN} = 45^\circ \). Thể tích nhỏ nhất của khối chóp \(S.AMN\) là

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Bạc Liêu 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(AB = 1\), cạnh bên \(SA = 1\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Kí hiệu \(M\) là điểm di động trên đoạn \(CD\) và \(N\) là điểm di động trên đoạn \(CB\) và góc \(\widehat {MAN} = 45^\circ \). Thể tích nhỏ nhất của khối chóp \(S.AMN\) là A. \(\frac{{\sqrt 2 - … [Đọc thêm...] về

(Sở Bạc Liêu 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông, \(AB = 1\), cạnh bên \(SA = 1\) và vuông góc với mặt đáy \(\left( {ABCD} \right)\). Kí hiệu \(M\) là điểm di động trên đoạn \(CD\) và \(N\) là điểm di động trên đoạn \(CB\) và góc \(\widehat {MAN} = 45^\circ \). Thể tích nhỏ nhất của khối chóp \(S.AMN\) là

(Sở Vĩnh Phúc 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, có \(AC = a\sqrt 3 ,\widehat {ABC} = {60^0}\). Biết rằng \(SA = SC\), \(SB = SD\) và khoảng cách từ \(A\) mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 6 }}{2}\). Tính thể tích khối chóp \(S.ABC\) bằng:

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Vĩnh Phúc 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, có \(AC = a\sqrt 3 ,\widehat {ABC} = {60^0}\). Biết rằng \(SA = SC\), \(SB = SD\) và khoảng cách từ \(A\) mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 6 }}{2}\). Tính thể tích khối chóp \(S.ABC\) bằng: A. \(\frac{{3\sqrt 6 {a^3}}}{8}\). B. \(\frac{{9\sqrt 6 … [Đọc thêm...] về

(Sở Vĩnh Phúc 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, có \(AC = a\sqrt 3 ,\widehat {ABC} = {60^0}\). Biết rằng \(SA = SC\), \(SB = SD\) và khoảng cách từ \(A\) mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 6 }}{2}\). Tính thể tích khối chóp \(S.ABC\) bằng: