Bài tập Hàm số

Đề: Cho hàm số: $y = \frac{{{x^2} – 2mx + 3{m^2}}}{{x – 2m}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số với $m = -1$.2) Xác định $m$ để hàm số (1) có hai khoảng đồng biến trong toàn miền xác định của nó.3) Xác định $m$ để hàm số (1) đồng biến trong khoảng $1 < x

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tính đơn điệu của hàm số

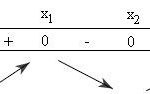
Đề bài: Cho hàm số: $y = \frac{{{x^2} - 2mx + 3{m^2}}}{{x - 2m}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số với $m = -1$.2) Xác định $m$ để hàm số (1) có hai khoảng đồng biến trong toàn miền xác định của nó.3) Xác định $m$ để hàm số (1) đồng biến trong khoảng $1 < x Lời giải Viết lại hàm số dưới dạng: $y = x + \frac{{3{m^2}}}{{x - … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{{x^2} – 2mx + 3{m^2}}}{{x – 2m}}$ (1)1) Khảo sát sự biến thiên và vẽ đồ thị hàm số với $m = -1$.2) Xác định $m$ để hàm số (1) có hai khoảng đồng biến trong toàn miền xác định của nó.3) Xác định $m$ để hàm số (1) đồng biến trong khoảng $1 < x

Đề: Tìm tập giá trị của các hàm số sau:a) $y=3\cos (x+\frac{\pi}{3} )+2$ b) $y=\sqrt{3+2\sin 2x} $c) $y=\frac{1}{\sin ^4 x+ \cos ^4 x} $ d) $y= \sqrt{1+\cos x}-3 $

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: Tìm tập giá trị của các hàm số sau:a) $y=3\cos (x+\frac{\pi}{3} )+2$ b) $y=\sqrt{3+2\sin 2x} $c) $y=\frac{1}{\sin ^4 x+ \cos ^4 x} $ d) $y= \sqrt{1+\cos x}-3 $ Lời giải a) Vì $-1 \leq \cos (x+\frac{\pi}{3} ) \leq 1$ nên $-3 \leq 3 \cos (x+\frac{\pi}{2} ) \leq … [Đọc thêm...] vềĐề: Tìm tập giá trị của các hàm số sau:a) $y=3\cos (x+\frac{\pi}{3} )+2$ b) $y=\sqrt{3+2\sin 2x} $c) $y=\frac{1}{\sin ^4 x+ \cos ^4 x} $ d) $y= \sqrt{1+\cos x}-3 $

Đề: Cho hàm số: $y = \frac{{2x^2 + x + 1}}{{x + 1}}\,\,\,\,\,(1)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số $(1)$.$2$. Tìm những điểm trên trục tung sao cho từ đó ta có thể vẽ được hai tiếp tuyến tới đồ thị hàm số $(1)$ và hai tiếp tuyến đó vuông góc với nhau.$3$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: $A = \frac{{2\cos^2x + |\cos x| + 1}}{{|\cos x| + 1}}$

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Khảo sát và vẽ đồ thị hàm số

Đề bài: Cho hàm số: $y = \frac{{2x^2 + x + 1}}{{x + 1}}\,\,\,\,\,(1)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số $(1)$.$2$. Tìm những điểm trên trục tung sao cho từ đó ta có thể vẽ được hai tiếp tuyến tới đồ thị hàm số $(1)$ và hai tiếp tuyến đó vuông góc với nhau.$3$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: $A = \frac{{2\cos^2x + |\cos x| + … [Đọc thêm...] vềĐề: Cho hàm số: $y = \frac{{2x^2 + x + 1}}{{x + 1}}\,\,\,\,\,(1)$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số $(1)$.$2$. Tìm những điểm trên trục tung sao cho từ đó ta có thể vẽ được hai tiếp tuyến tới đồ thị hàm số $(1)$ và hai tiếp tuyến đó vuông góc với nhau.$3$. Tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: $A = \frac{{2\cos^2x + |\cos x| + 1}}{{|\cos x| + 1}}$

Đề: TÌm giá trị lớn nhất và nhỏ nhất của:$y=\frac{3+8x^{2}+12x^{4}}{(1+2x^{2})^{2}}$

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: TÌm giá trị lớn nhất và nhỏ nhất của:$y=\frac{3+8x^{2}+12x^{4}}{(1+2x^{2})^{2}}$ Lời giải Đặt: $x=\frac{1}{\sqrt{2}}\tan \alpha, \alpha \in (-\frac{\pi}{2},\frac{\pi}{2})$$\Rightarrow x^2=\frac{1}{2}\tan^2\alpha, x^4=\frac{1}{4}\tan^4\alpha$$\Rightarrow y=(3+4\tan^{2} \alpha+3\tan^{4} … [Đọc thêm...] vềĐề: TÌm giá trị lớn nhất và nhỏ nhất của:$y=\frac{3+8x^{2}+12x^{4}}{(1+2x^{2})^{2}}$

Đề: Trong các nghiệm $(x,y)$ của bất phương trình : $\log _{x^2+y^2}(x+y)\geq 1$. Hãy tìm nghiệm có tổng $x+2y$ lớn nhất.

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: Trong các nghiệm $(x,y)$ của bất phương trình : $\log _{x^2+y^2}(x+y)\geq 1$. Hãy tìm nghiệm có tổng $x+2y$ lớn nhất. Lời giải Điều kiện của nghiệm: ${x^2} + {y^2} > 0,{\rm{ }}{x^2} + {y^2} \ne 1,{\rm{ x}} + y > 0$a) ${x^2} + {y^2} > 1$. Bất phương trình đã cho tương đương với: $x + y \ge {x^2} + {y^2}$ $(1)$Đặt $t = x + 2y \Rightarrow x = t - 2y$ … [Đọc thêm...] vềĐề: Trong các nghiệm $(x,y)$ của bất phương trình : $\log _{x^2+y^2}(x+y)\geq 1$. Hãy tìm nghiệm có tổng $x+2y$ lớn nhất.

Đề: Xét tính chẵn, lẻ của các hàm sốa) $y=\tan x+\sin 2x$b) $y=\cos x+ \sin ^{2}x$

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tính chẵn lẻ của hàm số

Đề bài: Xét tính chẵn, lẻ của các hàm sốa) $y=\tan x+\sin 2x$b) $y=\cos x+ \sin ^{2}x$ Lời giải a) $y=f\left ( x \right )= \tan x+\sin 2x$ có tập xác định : $D=R\setminus \left \{ \frac{\pi}{2}+k\pi/k\in Z \right.\left. \right \}$Ta có +) $x\in D\Leftrightarrow -x\in D$+) $\forall x\in D, f\left ( -x \right )= \tan \left ( -x \right )+ \sin \left ( -2x \right )=-\tan … [Đọc thêm...] vềĐề: Xét tính chẵn, lẻ của các hàm sốa) $y=\tan x+\sin 2x$b) $y=\cos x+ \sin ^{2}x$

Đề: Cho hàm số $y = x^3 + 3x^2 + mx + 1$ có đồ thị là $(C_m)$. Tìm $m$ để $(C_m)$ cắt đường $y = 1$ tại ba điểm phân biệt $C(0; 1), D, E$ sao cho tiếp tuyến tại $D, E$ vuông góc với nhau.

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tiếp tuyến của đồ thị

Đề bài: Cho hàm số $y = x^3 + 3x^2 + mx + 1$ có đồ thị là $(C_m)$. Tìm $m$ để $(C_m)$ cắt đường $y = 1$ tại ba điểm phân biệt $C(0; 1), D, E$ sao cho tiếp tuyến tại $D, E$ vuông góc với nhau. Lời giải Phương trình hoành độ giao điểm của 2 đường là: $ {{\rm{x}}^{\rm{3}}} + {\rm{ 3}}{{\rm{x}}^{\rm{2}}} + {\rm{ mx }} + {\rm{ 1 }} = {\rm{ 1}} \Leftrightarrow {\rm{x}}\left( … [Đọc thêm...] vềĐề: Cho hàm số $y = x^3 + 3x^2 + mx + 1$ có đồ thị là $(C_m)$. Tìm $m$ để $(C_m)$ cắt đường $y = 1$ tại ba điểm phân biệt $C(0; 1), D, E$ sao cho tiếp tuyến tại $D, E$ vuông góc với nhau.

Đề: Tìm:a) GTNN của $y=x^{2}-6x+5$ b)GTLN của $y=-2 x^{2}+3x-1 $c)GTNN của $y=(x-1)^{2}+(2x-3)^{2}+(3x-5)^{2} $ d)GTNN của $ T=2y-2x-2xy-2 x^{2}-2 y^{2}+7 $

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Giá trị lớn nhất - nhỏ nhất

Đề bài: Tìm:a) GTNN của $y=x^{2}-6x+5$ b)GTLN của $y=-2 x^{2}+3x-1 $c)GTNN của $y=(x-1)^{2}+(2x-3)^{2}+(3x-5)^{2} $ d)GTNN của $ T=2y-2x-2xy-2 x^{2}-2 y^{2}+7 $ Lời giải Hướng dẫn: dùng phương pháp nhóm bình phươngThêm lời giải chi tiết … [Đọc thêm...] vềĐề: Tìm:a) GTNN của $y=x^{2}-6x+5$ b)GTLN của $y=-2 x^{2}+3x-1 $c)GTNN của $y=(x-1)^{2}+(2x-3)^{2}+(3x-5)^{2} $ d)GTNN của $ T=2y-2x-2xy-2 x^{2}-2 y^{2}+7 $

Đề: Cho hàm số $y = x^3 + (1 – 2m)x^2 + (2 – m)x + m + 2 (C)$. Tìm m để hàm số có CĐ, CT thỏa mãn $x_{CT} < 2$

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Cực trị của hàm số

Đề bài: Cho hàm số $y = x^3 + (1 - 2m)x^2 + (2 - m)x + m + 2 (C)$. Tìm m để hàm số có CĐ, CT thỏa mãn $x_{CT} < 2$ Lời giải Ta có: $y' = 3{x^2} + 2(1 - 2m)x + (2 - m)$ Hàm số có CĐ, CT $ \Leftrightarrow y' = 0$ có 2 nghiệm phân biệt \( \Leftrightarrow \Delta ' = {(1 - 2m)^2} - 3(2 - m) = 4{m^2} - m - 5 > 0 \Leftrightarrow \left[ \begin{array}{l} m > \frac{5}{4}\\ m … [Đọc thêm...] vềĐề: Cho hàm số $y = x^3 + (1 – 2m)x^2 + (2 – m)x + m + 2 (C)$. Tìm m để hàm số có CĐ, CT thỏa mãn $x_{CT} < 2$

Đề: Cho $a,b$ là các số thực cho trước. Xác định tất cả các hàm số $f(x)$ thỏa mãn mỗi một tính chất sau đây:a) $f(a-x)=f(x)$, với mọi $x\in R$b) $f(a-x)+f(x)=b$, với mọi $x\in R$

Ngày 14/03/2020 Thuộc chủ đề:Bài tập Hàm số Tag với:Tính chất của hàm số

Đề bài: Cho $a,b$ là các số thực cho trước. Xác định tất cả các hàm số $f(x)$ thỏa mãn mỗi một tính chất sau đây:a) $f(a-x)=f(x)$, với mọi $x\in R$b) $f(a-x)+f(x)=b$, với mọi $x\in R$ Lời giải GiảiĐặt $x=\frac{a}{2}-t, t\in R$ suy ra $t=\frac{a}{2}-x$ và $a-x=\frac{a}{2}+t$. Ta cóa) $f(a-x)=f(x), \forall x\in R \Rightarrow f(\frac{a}{2}+1)=f(\frac{a}{2}-t), \forall t\in … [Đọc thêm...] vềĐề: Cho $a,b$ là các số thực cho trước. Xác định tất cả các hàm số $f(x)$ thỏa mãn mỗi một tính chất sau đây:a) $f(a-x)=f(x)$, với mọi $x\in R$b) $f(a-x)+f(x)=b$, với mọi $x\in R$