Đề bài: Cho hàm số $ y = \frac{2x - 1}{x + 1} (1)$. Tìm điểm $M$ thuộc đồ thị $(C)$ để tiếp tuyến của $(C)$ tại $M$ với đường thẳng đi qua $M$ và giao điểm hai đường tiệm cận có tích hệ số góc bằng $-9$. Lời giải +) Ta có I(- 1; 2). Gọi $ M \in (C) \Rightarrow M({x_0};2 - \frac{3}{{{x_0} + 1}}) \Rightarrow {k_{IM}} = \frac{{{y_M} - {y_I}}}{{{x_M} - {x_I}}} = \frac{{ - … [Đọc thêm...] vềĐề: Cho hàm số $ y = \frac{2x – 1}{x + 1} (1)$. Tìm điểm $M$ thuộc đồ thị $(C)$ để tiếp tuyến của $(C)$ tại $M$ với đường thẳng đi qua $M$ và giao điểm hai đường tiệm cận có tích hệ số góc bằng $-9$.
Bài tập Hàm số
Đề: Cho $f(x)=x^3$ và $g(x)=4x^2+\cos\pi x$. Tính $\frac{f'(1)}{g'(1)}$
Đề bài: Cho $f(x)=x^3$ và $g(x)=4x^2+\cos\pi x$. Tính $\frac{f'(1)}{g'(1)}$ Lời giải Ta có:$f'(x)=3x^2; f'(1)=3; g'(x)=8x-\pi\sin\pi x; g'(1)=8$ $\Rightarrow \frac{f'(1)}{g'(1)}=\frac{3}{8}$ … [Đọc thêm...] vềĐề: Cho $f(x)=x^3$ và $g(x)=4x^2+\cos\pi x$. Tính $\frac{f'(1)}{g'(1)}$
Đề: Cho $f:[0,1]\to [0,\to \infty ]$ liên tục.Đặt: $I_{n}=\int\limits^{1}_{0} f^{n}(x)dx,n\geq 3$Chứng minh rằng: $I^{2}_{n-1}\leq I_{n}.I_{n-2}$
Đề bài: Cho $f:[0,1]\to [0,\to \infty ]$ liên tục.Đặt: $I_{n}=\int\limits^{1}_{0} f^{n}(x)dx,n\geq 3$Chứng minh rằng: $I^{2}_{n-1}\leq I_{n}.I_{n-2}$ Lời giải Ta có: $I^{2}_{n-1}=[\int\limits^{1}_{0} f^{\frac{n}{2}}(x).f^{\frac{n-2}{2}}(x)dx]^{2}$$\leq \int\limits^{1}_{0} f^{n}(x)dx\int\limits^{1}_{0} f^{n-2}(x)dx=I_{n}.I_{n-2}$$\Rightarrow$ (ĐPCM) … [Đọc thêm...] vềĐề: Cho $f:[0,1]\to [0,\to \infty ]$ liên tục.Đặt: $I_{n}=\int\limits^{1}_{0} f^{n}(x)dx,n\geq 3$Chứng minh rằng: $I^{2}_{n-1}\leq I_{n}.I_{n-2}$
Đề: Cho hàm số $y = x^3 + (1 – 2m)x^2 + (2 – m)x + m + 2 (C).$ Tìm $m$ để hàm đồng biến trên $( 0; + \infty )$
Đề bài: Cho hàm số $y = x^3 + (1 - 2m)x^2 + (2 - m)x + m + 2 (C).$ Tìm $m$ để hàm đồng biến trên $( 0; + \infty )$ Lời giải Hàm đồng biến trên $\left( {0; + \infty } \right)$ $ \Leftrightarrow y' = 3{x^2} + 2(1 - 2m)x + (2 - m) \ge 0$ với $\forall x \in \left( {0; + \infty } \right)$Xét $ f\left( x \right) = \frac{{3{x^2} + 2x + 2}}{{4x + 1}} \ge m$ với $\forall x \in … [Đọc thêm...] vềĐề: Cho hàm số $y = x^3 + (1 – 2m)x^2 + (2 – m)x + m + 2 (C).$ Tìm $m$ để hàm đồng biến trên $( 0; + \infty )$
Đề: 1) Cho $y = \frac{{{x^2}}}{{1 – x}}$, tìm $y^{(8)}$2) Cho $y = \frac{1}{{{x^2} – 3x + 2}}$, tìm ${y^{(n)}}$.
Đề bài: 1) Cho $y = \frac{{{x^2}}}{{1 - x}}$, tìm $y^{(8)}$2) Cho $y = \frac{1}{{{x^2} - 3x + 2}}$, tìm ${y^{(n)}}$. Lời giải 1) Ta có:$y = \frac{{{x^2} - 1 + 1}}{{1 - x}} = - x - 1 - \frac{1}{{x - 1}} = - x - 1 - {(x - 1)^{ - 1}}$$ \Rightarrow y' = 1 - ( - 1).{(x - 1)^2}$ $y'' = - ( - 1).( - 2){(x - 1)^3} = {( - 1)^3}.2!{(x - 1)^{ - 3}}$$ \Rightarrow y''' = {( - … [Đọc thêm...] vềĐề: 1) Cho $y = \frac{{{x^2}}}{{1 – x}}$, tìm $y^{(8)}$2) Cho $y = \frac{1}{{{x^2} – 3x + 2}}$, tìm ${y^{(n)}}$.
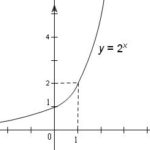
Đề: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$
Đề bài: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$ Lời giải $1)$.. Lập bảng biến thiên và vẽ đồ thị ($C$) của hàm số $y = {2^x}$ Đồ thị $({C^,})$của hàm số $y = {\left( {\frac{1}{2}} \right)^x}$ là đường đối xứng của ($C$) qua trục tung $Oy.$$2)$ Đồ thị $({C_1})$ của hàm số $y … [Đọc thêm...] vềĐề: Vẽ các đồ thị hàm số :$1)\,\,y = {2^x}\,$ và $y = {\left( {\frac{1}{2}} \right)^x}$$2)\,y = {\log _2}x$ và $y = {\log _{\frac{1}{2}}}x$
Đề: Xét tính liên tục của hàm số: $f(x)=\begin{cases} x^{3}+x+1;x\geq 1\\ 2x+4 ;x
Đề bài: Xét tính liên tục của hàm số: $f(x)=\begin{cases} x^{3}+x+1;x\geq 1\\ 2x+4 ;x Lời giải Dễ thấy ngay, hàm số liên tục trên các khoảng $(-\infty;3), (3;5), (5;+\infty)$.Chỉ cần xét tính liên tục của $f(x)$ tại điểm $x=3,x=5$. $\mathop {\lim }\limits_{x \to 3^-}f(x)=1; \mathop {\lim }\limits_{x \to 3^+}f(x)=3a+b ; f(3)=1 $Nên … [Đọc thêm...] vềĐề: Xét tính liên tục của hàm số: $f(x)=\begin{cases} x^{3}+x+1;x\geq 1\\ 2x+4 ;x
Đề: Tính đạo hàm số cấp $n$ của hàm số:a) $y=\ln x$b) $y=\ln(x^2+x-2).$
Đề bài: Tính đạo hàm số cấp $n$ của hàm số:a) $y=\ln x$b) $y=\ln(x^2+x-2).$ Lời giải a) Ta có $y'=(\ln x)'=\frac{1}{x}, y''=-\frac{1}{x^2}, y'''=\frac{1.2}{x^3}, y^{(4)}=-\frac{1.2.3}{x^4} $bằng phương pháp quy nạp, ta chứng minh được:$y^{(n)}=(-1)^{n+1.\frac{(n-1)!}{x^n} }, n\in \mathbb{Z} ^*$b) Điều kiện $x1$ Với điều kiện trên thì $x^2+x-2=(x-1)(x+2)>0$, do … [Đọc thêm...] vềĐề: Tính đạo hàm số cấp $n$ của hàm số:a) $y=\ln x$b) $y=\ln(x^2+x-2).$
Đề: Tìm đạo hàm cấp hai của mỗi hàm số sau:a) \(y=(x+3)(2x^{2}-x+1)\)b) \(y=\sqrt{x^{2}+1}\).
Đề bài: Tìm đạo hàm cấp hai của mỗi hàm số sau:a) \(y=(x+3)(2x^{2}-x+1)\)b) \(y=\sqrt{x^{2}+1}\). Lời giải a) \(y'=(x+3)'(2x^{2}-x+1)+(x+3)(2x^{2}-x+1)'=6x^{2}+10x-2\)\(y''=(6x^{2}+10x-2)'=12x+10\).b) … [Đọc thêm...] vềĐề: Tìm đạo hàm cấp hai của mỗi hàm số sau:a) \(y=(x+3)(2x^{2}-x+1)\)b) \(y=\sqrt{x^{2}+1}\).
Đề: $1$. Khảo sát hàm số \(y = – {x^4} + 5{x^2} – 4\)$2$. Xác định $m$ để phương trình \({x^4} – 5{x^2} – {m^2} + \sqrt 3 m = 0\) có $4$ nghiệm phân biệt
Đề bài: $1$. Khảo sát hàm số \(y = - {x^4} + 5{x^2} - 4\)$2$. Xác định $m$ để phương trình \({x^4} - 5{x^2} - {m^2} + \sqrt 3 m = 0\) có $4$ nghiệm phân biệt Lời giải $1$. Bạn đọc tự giải$2$. Đặt \(t = {x^2}\), phương trình đã cho trở thành \({t^2} - 5t - {m^2} + \sqrt 3 m = 0\left( 1 \right)\)Phương trình đã cho sẽ có 4 nghiệm phân biệt \( \Leftrightarrow \left( 1 … [Đọc thêm...] vềĐề: $1$. Khảo sát hàm số \(y = – {x^4} + 5{x^2} – 4\)$2$. Xác định $m$ để phương trình \({x^4} – 5{x^2} – {m^2} + \sqrt 3 m = 0\) có $4$ nghiệm phân biệt