Câu hỏi: 70. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(d:y = 2x\) quay xung quanh trục \(Ox\). A. \(\pi \int\limits_0^2 {{{\left( {{x^2} - 2x} \right)}^2}{\rm{d}}x} \). B. \(\pi \int\limits_0^2 {4{x^2}{\rm{d}}x} - \pi \int\limits_0^2 {{x^4}{\rm{d}}x} \). C. \(\pi … [Đọc thêm...] về70. Tìm công thức tính thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi parabol \(\left( P \right):y = {x^2}\) và đường thẳng \(d:y = 2x\) quay xung quanh trục \(Ox\).
Trắc nghiệm Tích phân
28. Gọi S là diện tích hình phẳng \(\left( H \right)\)giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và 2 đường thẳng \(x = – 1,\) \(x = 2\) trong hình vẽ bên.
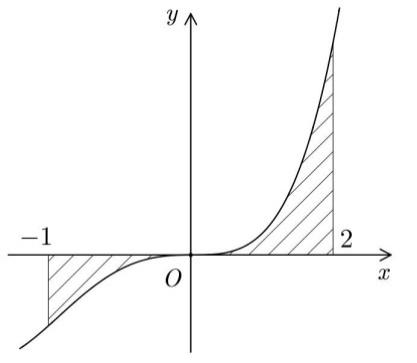
Đặt \({S_1} = \int\limits_{ – 1}^0 {f\left( x \right){\rm{d}}x} ,{S_2} = \int\limits_0^2 {f\left( x \right){\rm{d}}x} \). Mệnh đề nào sau đây đúng?
Câu hỏi: 28. Gọi S là diện tích hình phẳng \(\left( H \right)\)giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và 2 đường thẳng \(x = - 1,\) \(x = 2\) trong hình vẽ bên. Đặt \({S_1} = \int\limits_{ - 1}^0 {f\left( x \right){\rm{d}}x} ,{S_2} = \int\limits_0^2 {f\left( x \right){\rm{d}}x} \). Mệnh đề nào sau đây đúng? A. \(S = {S_1} + … [Đọc thêm...] về28. Gọi S là diện tích hình phẳng \(\left( H \right)\)giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và 2 đường thẳng \(x = – 1,\) \(x = 2\) trong hình vẽ bên.
Đặt \({S_1} = \int\limits_{ – 1}^0 {f\left( x \right){\rm{d}}x} ,{S_2} = \int\limits_0^2 {f\left( x \right){\rm{d}}x} \). Mệnh đề nào sau đây đúng?
12. Cho hàm số \(f\left( x \right)\) liên tục và có đạo hàm trên \(\left[ { – 1;2} \right]\). Biết \(f\left( { – 1} \right) = 1,\,f\left( 2 \right) = 8\), tính tích phân \(\int\limits_{ – 1}^2 {\left[ {2x + f’\left( x \right)} \right]} {\rm{d}}x\).
Câu hỏi: 12. Cho hàm số \(f\left( x \right)\) liên tục và có đạo hàm trên \(\left[ { - 1;2} \right]\). Biết \(f\left( { - 1} \right) = 1,\,f\left( 2 \right) = 8\), tính tích phân \(\int\limits_{ - 1}^2 {\left[ {2x + f'\left( x \right)} \right]} {\rm{d}}x\). A. \(12\). B. \(10\). C. \( - 4\). D. \( - 2\). Lời giải Ta có \(\int\limits_{ - 1}^2 {\left[ {2x + … [Đọc thêm...] về12. Cho hàm số \(f\left( x \right)\) liên tục và có đạo hàm trên \(\left[ { – 1;2} \right]\). Biết \(f\left( { – 1} \right) = 1,\,f\left( 2 \right) = 8\), tính tích phân \(\int\limits_{ – 1}^2 {\left[ {2x + f’\left( x \right)} \right]} {\rm{d}}x\).
10. Tìm họ nguyên hàm của hàm số \(f\left( x \right) = x{.2^x}\)
Câu hỏi: 10. Tìm họ nguyên hàm của hàm số \(f\left( x \right) = x{.2^x}\) A. \(\int {f\left( x \right)} {\rm{d}}x = {2^x}\ln x + C\). B. \(\int {f\left( x \right)} {\rm{d}}x = {2^x}\left( {1 + x.\ln 2} \right) + C\). C. \(\int {f\left( x \right)} {\rm{d}}x = \left( {x - \frac{1}{{\ln 2}}} \right).\frac{{{2^x}}}{{\ln 2}} + C\). D. \(\int {f\left( x … [Đọc thêm...] về10. Tìm họ nguyên hàm của hàm số \(f\left( x \right) = x{.2^x}\)
40. Biết \(F\left( x \right) = \frac{1}{{{x^2}}}\) là một nguyên hàm của \(\frac{{f\left( x \right)}}{x}\). Khẳng định nào sau đây đúng?
Câu hỏi: 40. Biết \(F\left( x \right) = \frac{1}{{{x^2}}}\) là một nguyên hàm của \(\frac{{f\left( x \right)}}{x}\). Khẳng định nào sau đây đúng? A. \(\int {f'\left( x \right){\rm{.}}\left( {{x^3} + 1} \right){\rm{d}}x = 4x + \frac{2}{{{x^2}}} + C} \). B. \(\int {f'\left( x \right){\rm{.}}\left( {{x^3} + 1} \right){\rm{d}}x = 4x - \frac{2}{{{x^2}}} + C} \). C. … [Đọc thêm...] về40. Biết \(F\left( x \right) = \frac{1}{{{x^2}}}\) là một nguyên hàm của \(\frac{{f\left( x \right)}}{x}\). Khẳng định nào sau đây đúng?
99. Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\). Tiếp tuyến \(d\) đi qua điểm \(A\) có hoành độ \(x = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm khác \(A\) có hoành độ lần lượt là \(x = – 4\) và \(x = 0\). Gọi \({S_1},{S_2}\) lần lượt là diện tích phần gạch sọc . Tính tỉ số \(\frac{{{S_2}}}{{{S_1}}}\).
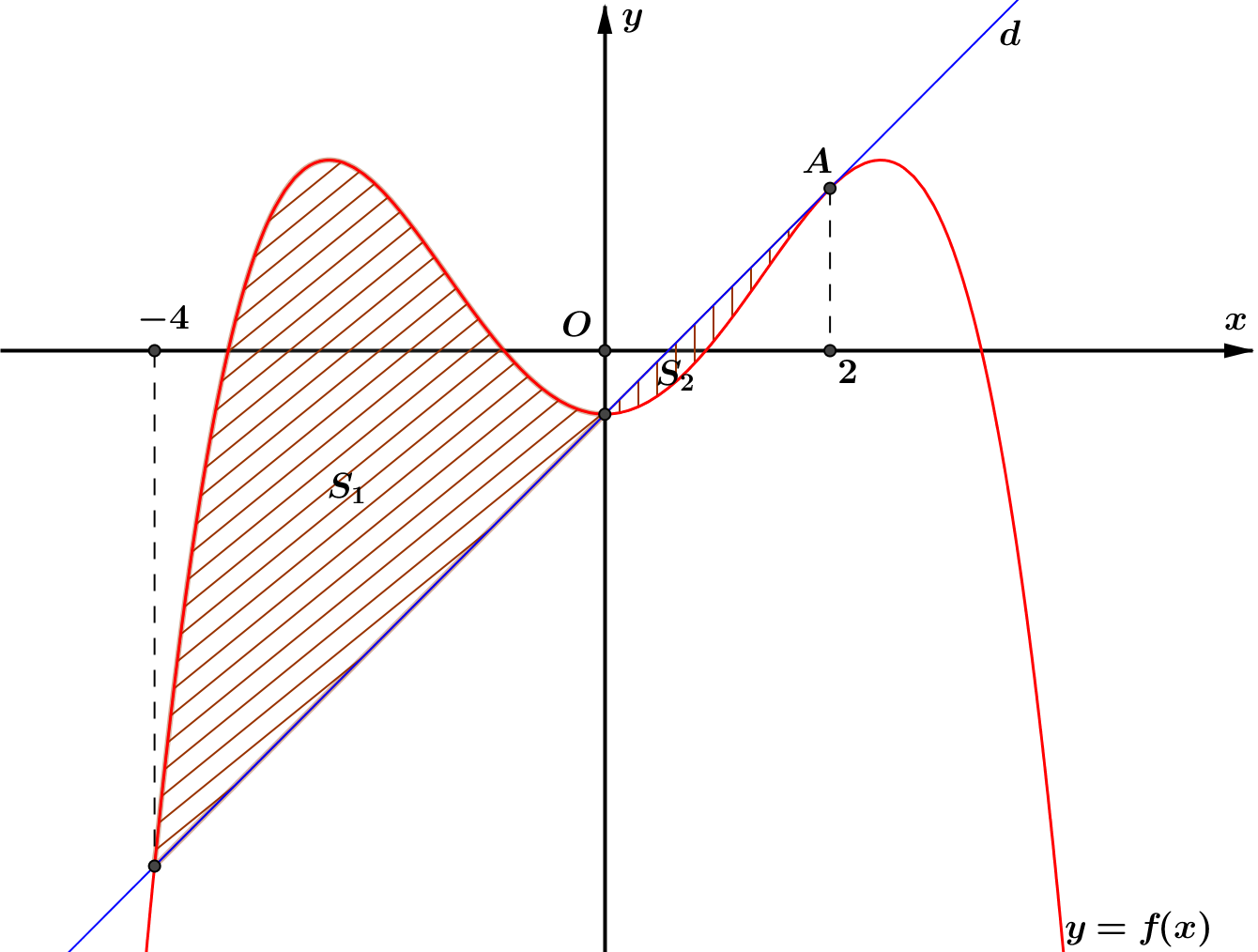
Câu hỏi: 99. Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\). Tiếp tuyến \(d\) đi qua điểm \(A\) có hoành độ \(x = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm khác \(A\) có hoành độ lần lượt là \(x = - 4\) và \(x = 0\). Gọi \({S_1},{S_2}\) lần lượt là diện tích phần gạch sọc . Tính tỉ số \(\frac{{{S_2}}}{{{S_1}}}\). A. … [Đọc thêm...] về99. Cho hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\). Tiếp tuyến \(d\) đi qua điểm \(A\) có hoành độ \(x = 2\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại hai điểm khác \(A\) có hoành độ lần lượt là \(x = – 4\) và \(x = 0\). Gọi \({S_1},{S_2}\) lần lượt là diện tích phần gạch sọc . Tính tỉ số \(\frac{{{S_2}}}{{{S_1}}}\).
3. Họ nguyên hàm của hàm số \(f\left( x \right) = \left( {{x^2} + x + 1} \right)\left( {2x + 1} \right)\) là
Câu hỏi: 3. Họ nguyên hàm của hàm số \(f\left( x \right) = \left( {{x^2} + x + 1} \right)\left( {2x + 1} \right)\) là A. \({\left( {{x^2} + x + 1} \right)^2} + C\). B. \( - \frac{1}{2}{\left( {{x^2} + x + 1} \right)^2} + C\). C.\(\frac{1}{2}{\left( {{x^2} + x + 1} \right)^2} + C\). D. \({\left( {2x + 1} \right)^2} + 2\left( {{x^2} + x + 1} \right) + C\). Lời … [Đọc thêm...] về3. Họ nguyên hàm của hàm số \(f\left( x \right) = \left( {{x^2} + x + 1} \right)\left( {2x + 1} \right)\) là
67. Tính thể tích \(V\) của vật thể giới hạn bởi hai mặt phẳng có phương trình \(x = 1\) và \(x = 3\), biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {1 \le x \le 3} \right)\) là hình vuông có cạnh \(\sqrt {3 – x} \).
Câu hỏi: 67. Tính thể tích \(V\) của vật thể giới hạn bởi hai mặt phẳng có phương trình \(x = 1\) và \(x = 3\), biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {1 \le x \le 3} \right)\) là hình vuông có cạnh \(\sqrt {3 - x} \). A. \(1\). B. \(2\). C. \(\pi \). D. \(2\pi \). Lời giải Theo giả … [Đọc thêm...] về67. Tính thể tích \(V\) của vật thể giới hạn bởi hai mặt phẳng có phương trình \(x = 1\) và \(x = 3\), biết rằng thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {1 \le x \le 3} \right)\) là hình vuông có cạnh \(\sqrt {3 – x} \).
68. Cho phần vật thể \(B\) giới hạn bởi hai mặt phẳng có phương trình \(x = 0\) và \(x = \frac{\pi }{3}\). Cắt phần vật thể \(B\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le \frac{\pi }{3}} \right)\) ta được thiết diện là một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là \(2x\) và \(\cos x\). Thể tích vật thể \(B\) bằng:
Câu hỏi: 68. Cho phần vật thể \(B\) giới hạn bởi hai mặt phẳng có phương trình \(x = 0\) và \(x = \frac{\pi }{3}\). Cắt phần vật thể \(B\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le \frac{\pi }{3}} \right)\) ta được thiết diện là một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là \(2x\) và \(\cos x\). Thể tích vật thể … [Đọc thêm...] về68. Cho phần vật thể \(B\) giới hạn bởi hai mặt phẳng có phương trình \(x = 0\) và \(x = \frac{\pi }{3}\). Cắt phần vật thể \(B\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le \frac{\pi }{3}} \right)\) ta được thiết diện là một tam giác vuông có độ dài hai cạnh góc vuông lần lượt là \(2x\) và \(\cos x\). Thể tích vật thể \(B\) bằng:
63. Giả sử \(I = \int\limits_3^4 {\left( {x – 2} \right)\ln \left( {x – 1} \right){\rm{d}}x} = \frac{{a\ln 3 – b}}{c},\) trong đó \(a,{\rm{ }}b,{\rm{ }}c\) là các số nguyên và \(\left( {b,c} \right) = 1\). Tính \(S = a + 2b + c.\)
Câu hỏi: 63. Giả sử \(I = \int\limits_3^4 {\left( {x - 2} \right)\ln \left( {x - 1} \right){\rm{d}}x} = \frac{{a\ln 3 - b}}{c},\) trong đó \(a,{\rm{ }}b,{\rm{ }}c\) là các số nguyên và \(\left( {b,c} \right) = 1\). Tính \(S = a + 2b + c.\) A. \(S = 8\). B. \(S = 12\). C. \(S = 10\). D.\(S = 11\). Lời giải Đặt \(\left\{ \begin{array}{l}u = \ln \left( {x … [Đọc thêm...] về63. Giả sử \(I = \int\limits_3^4 {\left( {x – 2} \right)\ln \left( {x – 1} \right){\rm{d}}x} = \frac{{a\ln 3 – b}}{c},\) trong đó \(a,{\rm{ }}b,{\rm{ }}c\) là các số nguyên và \(\left( {b,c} \right) = 1\). Tính \(S = a + 2b + c.\)
