Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số

Hàm số $y= f(x) = 6x^4-3x^2-18$ đạt giá trị lớn nhất trên đoạn $[-1, 8]$ bằng

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Bài toán gốc Hàm số $y= f(x) = 6x^4-3x^2-18$ đạt giá trị lớn nhất trên đoạn $[-1, 8]$ bằngA. $\max\limits_{x \in [-1, 8]} f(x) = 54$.B. $\max\limits_{x \in [-1, 8]} f(x) = 24366$.C. $\max\limits_{x \in [-1, 8]} f(x) = -\dfrac{147}{8}$.D. $\max\limits_{x \in [-1, 8]} f(x) = -138$.Lời giải: Trên đoạn $[-1, 8]$, ta có Đạo hàm $f^{\prime}(x) = 24x^3-6x$. Cho $f^{\prime}(x)= … [Đọc thêm...] vềHàm số $y= f(x) = 6x^4-3x^2-18$ đạt giá trị lớn nhất trên đoạn $[-1, 8]$ bằng

Cho hàm số $y=f(x)=-2x^4-2044x^2+2473$. Giá trị lớn nhất của hàm số trên $[-66;89]$ bằng

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Bài toán gốc Cho hàm số $y=f(x)=-2x^4-2044x^2+2473$. Giá trị lớn nhất của hàm số trên $[-66;89]$ bằng A. $2473$.B. $2475$.C. $2472$.D. $2476$.Lời giải: Hạn chế máy tính Phân tích và Phương pháp giải Đây là bài toán tìm giá trị lớn nhất (GTLN) của hàm số bậc bốn trùng phương $y = Ax^4 + Bx^2 + C$ trên một đoạn cho trước. Trong hàm số … [Đọc thêm...] vềCho hàm số $y=f(x)=-2x^4-2044x^2+2473$. Giá trị lớn nhất của hàm số trên $[-66;89]$ bằng

Tìm giá trị lớn nhất của hàm số $y=f(x)$ trên $[-2;2]$ có đồ thị như hình dưới đây

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Bài toán gốc Tìm giá trị lớn nhất của hàm số $y=f(x)$ trên $[-2;2]$ có đồ thị như hình dưới đâyA. -2.B. 0.C. 2.D. -1.Lời giải: $y=f(x)=x^3-3x$ Phân tích và Phương pháp giải Bài toán yêu cầu tìm giá trị lớn nhất (GTLN) của hàm số trên một đoạn đóng. Phương pháp giải chung là sử dụng đạo hàm để tìm các điểm cực trị nằm trong đoạn, sau đó tính giá … [Đọc thêm...] vềTìm giá trị lớn nhất của hàm số $y=f(x)$ trên $[-2;2]$ có đồ thị như hình dưới đây

Cho hàm số $y = f(x) = \dfrac{-2x^2-3x}{-2x+1}$. Khi đó giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên $[1, 6]$ lần lượt bằng

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Bài toán gốc Cho hàm số $y = f(x) = \dfrac{-2x^2-3x}{-2x+1}$. Khi đó giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên $[1, 6]$ lần lượt bằngA. $\max\limits_{[1, 6]}f(x) = \dfrac{90}{11}$, $\min\limits_{[1, 6]}f(x) = \dfrac{9}{2}$.B. $\max\limits_{[1, 6]}f(x) = -1$, $\min\limits_{[1, 6]}f(x) = \dfrac{9}{2}$.C. $\max\limits_{[1, 6]}f(x) = -1$, $\min\limits_{[1, 6]}f(x) … [Đọc thêm...] vềCho hàm số $y = f(x) = \dfrac{-2x^2-3x}{-2x+1}$. Khi đó giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên $[1, 6]$ lần lượt bằng

Giá trị nhỏ nhất của hàm số $y=x+\dfrac{25}{x}$ trên $[2;8]$ bằng

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Bài toán gốc Giá trị nhỏ nhất của hàm số $y=x+\dfrac{25}{x}$ trên $[2;8]$ bằngA. $\dfrac{89}{8}$.B. $10$.C. $-20$.D. $\dfrac{29}{2}$. Phân tích và Phương pháp giải Đây là bài toán tìm giá trị lớn nhất, nhỏ nhất của hàm số liên tục trên một đoạn kín (khoảng đóng). Phương pháp giải chuẩn là sử dụng đạo hàm:1. Tính đạo hàm $f'(x)$.2. Tìm các điểm … [Đọc thêm...] vềGiá trị nhỏ nhất của hàm số $y=x+\dfrac{25}{x}$ trên $[2;8]$ bằng

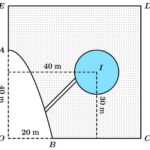
Một cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l (đơn vị mét) của cây cầu là bao nhiêu (làm tròn đến chữ số hàng phần chục), biết:

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

- Hai bờ AE và BC nằm trên hai đường thẳng vuông góc với nhau, hai đường thẳng này cắt nhau tại điểm O; - Bờ AB là một phần của một parabol có đỉnh là điểm A và có trục đối xứng là đường thẳng OA ; - Độ dài đoạn OA và OB lần lượt là 40m và 20m; - Tâm I của mảnh vườn cách đường … [Đọc thêm...] vềMột cái ao có hình ABCDE (như hình vẽ), ở giữa ao có một mảnh vườn hình tròn bán kính 10m, người ta muốn bắc một cây cầu từ bờ AB của ao đến vườn. Hỏi độ dài ngắn nhất l (đơn vị mét) của cây cầu là bao nhiêu (làm tròn đến chữ số hàng phần chục), biết:

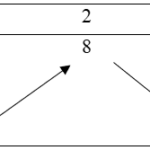
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x} + \sqrt {10 – 2x} = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)?

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:, ,

Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x}  + \sqrt {10 - 2x}  = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)? A . 4. B. 7.                              C.   6 . … [Đọc thêm...] vềCho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0\,;\,5} \right]\) và có bảng biến thiên như hình vẽ dưới đây Có bao nhiêu giá trị nguyên của \(m\) để phương trình \(\sqrt {3x} + \sqrt {10 – 2x} = m\sqrt {f\left( x \right)} \) có nghiệm trên đoạn \(\left[ {0\,;\,5} \right]\)?

Đề toán 2022 [2D1-3.1-3] Cho hàm số \(f\left( x \right) = m{x^4} + 2\left( {m – 1} \right){x^2}\) với \(m\)là tham số thực. Nếu \(\mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 1 \right)\) thì  \(\mathop {{\rm{max}}}\limits_{\left[ {0;2} \right]} f\left( x \right)\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:,

Đề toán 2022 [2D1-3.1-3] Cho hàm số \(f\left( x \right) = m{x^4} + 2\left( {m - 1} \right){x^2}\) với \(m\)là tham số thực. Nếu \(\mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 1 \right)\) thì  \(\mathop {{\rm{max}}}\limits_{\left[ {0;2} \right]} f\left( x \right)\) bằng A. \(2\). B. \( - 1\). C. \(4\). D. \(0\). Lời giải Nếu \(m \ge 1\) … [Đọc thêm...] về

Đề toán 2022 [2D1-3.1-3] Cho hàm số \(f\left( x \right) = m{x^4} + 2\left( {m – 1} \right){x^2}\) với \(m\)là tham số thực. Nếu \(\mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 1 \right)\) thì  \(\mathop {{\rm{max}}}\limits_{\left[ {0;2} \right]} f\left( x \right)\) bằng

Đề toán 2022 [Mức độ 3] Cho hàm số \(f\left( x \right) = \left( {m – 1} \right){x^4} – 2m{x^2} + 1\) với \(m\) là tham số thực. 

Nếu  \(\mathop {\min }\limits_{\left[ {0\,;\,3} \right]} f\left( x \right) = f\left( 2 \right)\) thì \(\mathop {\max }\limits_{\left[ {0\,;\,3} \right]} f\left( x \right)\)  bằng 

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Đề toán 2022 [Mức độ 3] Cho hàm số \(f\left( x \right) = \left( {m - 1} \right){x^4} - 2m{x^2} + 1\) với \(m\) là tham số thực.  Nếu  \(\mathop {\min }\limits_{\left[ {0\,;\,3} \right]} f\left( x \right) = f\left( 2 \right)\) thì \(\mathop {\max }\limits_{\left[ {0\,;\,3} \right]} f\left( x \right)\)  bằng  A. \( - \frac{{13}}{3}\). B. 4. C. \( - … [Đọc thêm...] về

Đề toán 2022 [Mức độ 3] Cho hàm số \(f\left( x \right) = \left( {m – 1} \right){x^4} – 2m{x^2} + 1\) với \(m\) là tham số thực. 

Nếu  \(\mathop {\min }\limits_{\left[ {0\,;\,3} \right]} f\left( x \right) = f\left( 2 \right)\) thì \(\mathop {\max }\limits_{\left[ {0\,;\,3} \right]} f\left( x \right)\)  bằng 

Đề toán 2022 [Mức độ 3] Cho hàm số \(f\left( x \right) = a{x^4} + 2\left( {a + 4} \right){x^2} – 1\) với \(a\) là tham số thực.

Nếu \(\mathop {\max }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right) = f\left( 1 \right)\) thì \(\mathop {\min }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right)\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Giá trị lớn nhất và nhỏ nhất của hàm số Tag với:

Đề toán 2022 [Mức độ 3] Cho hàm số \(f\left( x \right) = a{x^4} + 2\left( {a + 4} \right){x^2} - 1\) với \(a\) là tham số thực. Nếu \(\mathop {\max }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right) = f\left( 1 \right)\) thì \(\mathop {\min }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right)\) bằng A. \( - 17\). B. \( - 16\). C. \( - 1\). D. \(3\). Lời giải Ta … [Đọc thêm...] về

Đề toán 2022 [Mức độ 3] Cho hàm số \(f\left( x \right) = a{x^4} + 2\left( {a + 4} \right){x^2} – 1\) với \(a\) là tham số thực.

Nếu \(\mathop {\max }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right) = f\left( 1 \right)\) thì \(\mathop {\min }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right)\) bằng