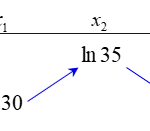
Đề toán 2022 [Mức độ 3] Cho hàm số bậc bốn \(y = f\left( x \right)\). Biết rằng hàm số \(g\left( x \right) = \ln f\left( x \right)\) có bảng biến thiên như sau:
Diện tích hình phẳng giới hạn bởi các đường \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) thuộc khoảng nào dưới đây?
A. \(\left( {33;35} \right)\). B. \(\left( {37;40} \right)\). C. \(\left( {29;32} … [Đọc thêm...] về
Đề toán 2022 [2D3-3.1-3] Biết \(F\left( x \right)\) và \(G\left( x \right)\) là hai nguyên hàm của hàm số \(f\left( x \right)\) trên \(\mathbb{R}\)và \(\int\limits_0^5 {f\left( x \right)dx} = F\left( 5 \right) - G\left( 0 \right) + a\) \(\left( {a > 0} \right)\). Gọi \(S\) là diện tích hình bẳng giới hạn bởi các đường \(y = F\left( x \right),y = G\left( x \right),x = … [Đọc thêm...] về
Đề toán 2022 [Mức độ 3] Có bao nhiêu số nguyên dương \(a\) sao cho ứng với mỗi \(a\) có đúng hai số nguyên \(b\) thỏa mãn \(\left( {{3^b} - 3} \right)\left( {a{{.2}^b} - 16} \right) < 0?\)
A. \(34\). B. \(32\). C. \(31\). D. \(33\).
Lời giải
Ta có: \(a \in {\mathbb{Z}^ + } \Rightarrow a \ge 1;\,b \in Z\)
\(\left( {{3^b} - 3} \right)\left( {a{{.2}^b} - 16} \right) … [Đọc thêm...] về
Câu hỏi:
(THPT Kim Liên - Hà Nội - 2022) Trong không gian \(Oxyz\), cho hai điểm \(A\left( { - 1;2;3} \right)\) và \(B\left( {3;2;5} \right)\). Xét hai điểm \(M\) và \(N\) thay đổi thuộc mặt phẳng \(\left( {Oxy} \right)\) sao cho \(MN = 2023\). Tìm giá trị nhỏ nhất của \(AM + BN\).
A. \(2\sqrt {17} \).
B. \(\sqrt {65} \).
C. \(25\sqrt {97} \).
D. \(205\sqrt … [Đọc thêm...] về
Câu hỏi:
(THPT Hương Sơn - Hà Tĩnh - 2022) Trong không gian với hệ toạ độ \(Oxyz\), cho mặt phẳng \(\left( \alpha \right):\;x + y - 2z - 2 = 0\) và đường thẳng \(\Delta :\;\frac{x}{2} = \frac{{y + 2}}{{ - 2}} = \frac{{z - 2}}{1} \cdot \) Đường thẳng \(\Delta '\) là hình chiếu vuông góc của đường thẳng \(\Delta \) trên mặt phẳng \(\left( \alpha \right)\) có phương … [Đọc thêm...] về
Câu hỏi:
(THPT Kim Liên - Hà Nội - 2022) Trong không gian \(Oxyz\), cho mặt phẳng \(\left( P \right):2x + 2y + z + 5 = 0\) và mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2; - 2} \right)\). Biết \(\left( P \right)\) cắt \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có chu vi \(8\pi \). Tìm bán kính của mặt cầu \(\left( T \right)\) chứa đường … [Đọc thêm...] về
Câu hỏi:
(THPT Hồ Nghinh – Quảng Nam – 2022) Trong không gian với hệ trục tọa độ \(Oxyz\), cho ba mặt phẳng \((P):x + y + z + 5 = 0\); \((Q):x + y + z + 1 = 0\) và \((R):x + y + z + 2 = 0\). Úng với mỗi cặp điểm \(A,B\) lần lượt thuộc hai mặt phẳng \((P),(Q)\) thì mặt cầu đường kinh \(AB\) luôn cắt mặt phẳng \((R)\) theo một đường tròn. Tìm bán kính nhỏ nhất của đường tròn … [Đọc thêm...] về
Câu hỏi:
(THPT Kinh Môn - Hải Dương - 2022) Trong không gian \(Oxyz\), cho mặt cầu \(\left( {{S_1}} \right)\) có tâm \(I\left( {2;1;1} \right)\) có bán kính bằng \(4\) và mặt cầu
\(\left( {{S_2}} \right)\) có tâm \(J\left( {2;1;5} \right)\) có bán kính bằng 2. Gọi \(\left( P \right)\) là mặt phẳng thay đổi tiếp xúc với hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} … [Đọc thêm...] về
Câu hỏi:
(Sở Hà Tĩnh 2022) Trong không gian \(Oxyz\), cho hai mặt cầu \(\left( {{S_1}} \right):{x^2} + {(y - 1)^2} + {(z - 2)^2} = 16;\left( {{S_2}} \right):{(x - 1)^2} + {(y + 1)^2} + {z^2} = 1\) và điểm \(A\left( {\frac{4}{3};\frac{7}{3}; - \frac{{14}}{3}} \right)\). Gọi \((P)\) là mặt phẳng tiếp xúc với cả hai mặt cầu \(\left( {{S_1}} \right),\left( {{S_2}} \right)\) và … [Đọc thêm...] về
Câu hỏi:
(Cụm Trường Nghệ An - 2022) Trong không gian \(Oxyz\), cho các điểm \(A\left( {0;0;3} \right)\) và \(B\left( {2; - 3; - 5} \right)\). Gọi \(\left( P \right)\) là mặt phẳng chứa đường tròn giao tuyến của hai mặt cầu \(\left( {{S_1}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 3} \right)^2} = 25\) và \(\left( {{S_2}} \right):{x^2} … [Đọc thêm...] về
