Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

The tich da dien VDC

(Sở Vĩnh Phúc 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, có \(AC = a\sqrt 3 ,\widehat {ABC} = {60^0}\). Biết rằng \(SA = SC\), \(SB = SD\) và khoảng cách từ \(A\) mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 6 }}{2}\). Tính thể tích khối chóp \(S.ABC\) bằng:

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Sở Vĩnh Phúc 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, có \(AC = a\sqrt 3 ,\widehat {ABC} = {60^0}\). Biết rằng \(SA = SC\), \(SB = SD\) và khoảng cách từ \(A\) mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 6 }}{2}\). Tính thể tích khối chóp \(S.ABC\) bằng: A. \(\frac{{3\sqrt 6 {a^3}}}{8}\). B. \(\frac{{9\sqrt 6 … [Đọc thêm...] về

(Sở Vĩnh Phúc 2022) Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, có \(AC = a\sqrt 3 ,\widehat {ABC} = {60^0}\). Biết rằng \(SA = SC\), \(SB = SD\) và khoảng cách từ \(A\) mặt phẳng \(\left( {SBC} \right)\) bằng \(\frac{{a\sqrt 6 }}{2}\). Tính thể tích khối chóp \(S.ABC\) bằng:

(Chuyên Lam Sơn 2022) Cho khối bát diện đều có cạnh \(a\). Gọi \(M,N,P,Q\) lần lượt là trọng tâm của các tam giác \(SAB,SBC,SCD,SDA;\) gọi \(M\prime ,N\prime ,P\prime ,Q\prime \) lần lượt là trọng tâm của các tam giác \(S\prime AB,S\prime BC,S\prime CD,S\prime DA\) (như hình vẽ dưới).

Thể tích của khối lăng trụ \(MNPQ \cdot M\prime N\prime P\prime Q\prime \) là

Ngày Thuộc chủ đề:Trắc nghiệm Thể tích đa diện Tag với:,

Câu hỏi: (Chuyên Lam Sơn 2022) Cho khối bát diện đều có cạnh \(a\). Gọi \(M,N,P,Q\) lần lượt là trọng tâm của các tam giác \(SAB,SBC,SCD,SDA;\) gọi \(M\prime ,N\prime ,P\prime ,Q\prime \) lần lượt là trọng tâm của các tam giác \(S\prime AB,S\prime BC,S\prime CD,S\prime DA\) (như hình vẽ dưới). Thể tích của khối lăng trụ \(MNPQ \cdot M\prime N\prime P\prime Q\prime \) … [Đọc thêm...] về

(Chuyên Lam Sơn 2022) Cho khối bát diện đều có cạnh \(a\). Gọi \(M,N,P,Q\) lần lượt là trọng tâm của các tam giác \(SAB,SBC,SCD,SDA;\) gọi \(M\prime ,N\prime ,P\prime ,Q\prime \) lần lượt là trọng tâm của các tam giác \(S\prime AB,S\prime BC,S\prime CD,S\prime DA\) (như hình vẽ dưới).

Thể tích của khối lăng trụ \(MNPQ \cdot M\prime N\prime P\prime Q\prime \) là

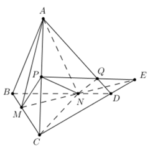
Cho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\)

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:, ,

Cho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\). Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\) A. \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{26}}{{19}}\) … [Đọc thêm...] vềCho tứ diện \(ABCD\), trên các cạnh \(BC,\,\,BD,\,\,AC\) lần lượt lấy các điểm \(M,\,\,N,\,\,P\) sao cho \(BC = 3BM,\,\,BD = \dfrac{3}{2}BN,\,\,AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện \(ABCD\) thành 2 phần có thể tích là \({V_1},\,\,{V_2}\)

Cho hình chóp S.ABCD có \(SC = x\,\,\left( {0 < x < a\sqrt 3 } \right)\), các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi \(x = \dfrac{{a\sqrt m }}{n}\,\,\left( {m,n \in {N^*}} \right)\). Mệnh đề nào sau đây đúng?

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho hình chóp S.ABCD có \(SC = x\,\,\left( {0 < x < a\sqrt 3 } \right)\), các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi \(x = \dfrac{{a\sqrt m }}{n}\,\,\left( {m,n \in {N^*}} \right)\). Mệnh đề nào sau đây đúng?  A. \(m + 2n = … [Đọc thêm...] vềCho hình chóp S.ABCD có \(SC = x\,\,\left( {0 < x < a\sqrt 3 } \right)\), các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi \(x = \dfrac{{a\sqrt m }}{n}\,\,\left( {m,n \in {N^*}} \right)\). Mệnh đề nào sau đây đúng?

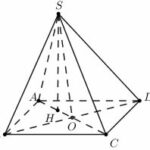
Cho hình chóp tứ giác đều\(S.ABCD\)có góc giữa cạnh bên và mặt đáy bằng\({60^\circ }\). Gọi\(O\)là tâm của hình vuông\(ABCD\). Biết diện tích tam giác\(OAB\)bằng\(2{a^2}\), tính thể tích khối chóp đã cho.

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho hình chóp tứ giác đều\(S.ABCD\)có góc giữa cạnh bên và mặt đáy bằng\({60^\circ }\). Gọi\(O\)là tâm của hình vuông\(ABCD\). Biết diện tích tam giác\(OAB\)bằng\(2{a^2}\), tính thể tích khối chóp đã cho. A. \(16{a^3}\sqrt 3 \). B. \(\frac{{16{a^3}}}{3}\). C\(\frac{{16{a^3}\sqrt 3 }}{3}\). D. \(16{a^3}\). LỜI GIẢI CHI TIẾT Ta có\({S_{ABCD}} = … [Đọc thêm...] về

Cho hình chóp tứ giác đều\(S.ABCD\)có góc giữa cạnh bên và mặt đáy bằng\({60^\circ }\). Gọi\(O\)là tâm của hình vuông\(ABCD\). Biết diện tích tam giác\(OAB\)bằng\(2{a^2}\), tính thể tích khối chóp đã cho.

Cho lăng trụ\(ABC. A’B’C’\)có đáy\(ABC\)là tam giác vuông tại\(A\),\(AB = 1,AC = 2\). Hình chiếu của\(A’\)lên mặt phẳng\((ABC)\)trùng với trung điểm cạnh\(BC\). Biết khoảng cách giữa hai đường thẳng\(CC’\)và\(A’B\)là\(\sqrt 2 \). Thể tích khối lăng trụ\(ABC. A’B’C’\) bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho lăng trụ\(ABC. A'B'C'\)có đáy\(ABC\)là tam giác vuông tại\(A\),\(AB = 1,AC = 2\). Hình chiếu của\(A'\)lên mặt phẳng\((ABC)\)trùng với trung điểm cạnh\(BC\). Biết khoảng cách giữa hai đường thẳng\(CC'\)và\(A'B\)là\(\sqrt 2 \). Thể tích khối lăng trụ\(AB C. A'B'C'\) bằng A. \(\frac{1}{2}\). B. \(\frac{{\sqrt 2 }}{3}\). C. \(\sqrt 2 \). D. 1. LỜI … [Đọc thêm...] về

Cho lăng trụ\(ABC. A’B’C’\)có đáy\(ABC\)là tam giác vuông tại\(A\),\(AB = 1,AC = 2\). Hình chiếu của\(A’\)lên mặt phẳng\((ABC)\)trùng với trung điểm cạnh\(BC\). Biết khoảng cách giữa hai đường thẳng\(CC’\)và\(A’B\)là\(\sqrt 2 \). Thể tích khối lăng trụ\(ABC. A’B’C’\) bằng

Cho hình chóp tam giác \(S.ABC\), \(SA \bot \left( {ABC} \right)\). Đáy \(ABC\) là tam giác vuông cân đỉnh \(B\), \(SB = a\). Gọi \(\alpha \) là góc giữa hai mặt phẳng và \(\left( {ABC} \right)\). Xác định giá trị của \(\sin \alpha \) để thể tích khối chóp \(S.ABC\) lớn nhất.

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho hình chóp tam giác \(S.ABC\), \(SA \bot \left( {ABC} \right)\). Đáy \(ABC\) là tam giác vuông cân đỉnh \(B\), \(SB = a\). Gọi \(\alpha \) là góc giữa hai mặt phẳng và \(\left( {ABC} \right)\). Xác định giá trị của \(\sin \alpha \) để thể tích khối chóp \(S.ABC\) lớn nhất. A. \(\sin \alpha= \frac{{\sqrt 3 }}{3}.\) B. \(\sin \alpha= \frac{{2\sqrt 3 … [Đọc thêm...] về

Cho hình chóp tam giác \(S.ABC\), \(SA \bot \left( {ABC} \right)\). Đáy \(ABC\) là tam giác vuông cân đỉnh \(B\), \(SB = a\). Gọi \(\alpha \) là góc giữa hai mặt phẳng và \(\left( {ABC} \right)\). Xác định giá trị của \(\sin \alpha \) để thể tích khối chóp \(S.ABC\) lớn nhất.

Cho tứ diện\(ABCD\)có\(AB = AC = BD = CD = 1\). Khi thể tích của khối tứ diện lớn nhất thì khoảng cách giữa hai đường thẳng\(AD\)và\(BC\)bằng

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho tứ diện\(ABCD\)có\(AB = AC = BD = CD = 1\). Khi thể tích của khối tứ diện lớn nhất thì khoảng cách giữa hai đường thẳng\(AD\)và\(BC\)bằng A. \(\frac{{\sqrt 2 }}{2}\). B. \(\frac{{2\sqrt 3 }}{3}\). C. \(\frac{{\sqrt 3 }}{6}\). D. \(\frac{{\sqrt 3 }}{3}\). LỜI GIẢI CHI TIẾT Gọi\(H\),\(K\)lần lượt là trung điểm của\(BC\)và\(AD\). Vì\(AB = … [Đọc thêm...] về

Cho tứ diện\(ABCD\)có\(AB = AC = BD = CD = 1\). Khi thể tích của khối tứ diện lớn nhất thì khoảng cách giữa hai đường thẳng\(AD\)và\(BC\)bằng

Cho hình chóp\(S.ABCD\)có đáy là hình bình hành. Gọi\(M,N,P,Q\)lần lượt là trọng tâm của các tam giác\(SAB,SBC,SCD,SDA\). Gọi\(O\)là điểm bất kỳ trên mặt phẳng đáy\(ABCD\). Biết thể tích khối chóp\(O.MNPQ\)bằng\(V\). Tính thể tích khối chóp\(S.ABCD\).

Ngày Thuộc chủ đề:Trắc nghiệm Khối đa diện Tag với:,

Câu hỏi: Cho hình chóp\(S.ABCD\)có đáy là hình bình hành. Gọi\(M,N,P,Q\)lần lượt là trọng tâm của các tam giác\(SAB,SBC,SCD,SDA\). Gọi\(O\)là điểm bất kỳ trên mặt phẳng đáy\(ABCD\). Biết thể tích khối chóp\(O.MNPQ\)bằng\(V\). Tính thể tích khối chóp\(S.ABCD\). A. \(\frac{{27}}{8}V\). B. \(\frac{{27}}{2}V\). C. \(\frac{9}{4}V\). D. \(\frac{{27}}{4}V\). LỜI … [Đọc thêm...] về

Cho hình chóp\(S.ABCD\)có đáy là hình bình hành. Gọi\(M,N,P,Q\)lần lượt là trọng tâm của các tam giác\(SAB,SBC,SCD,SDA\). Gọi\(O\)là điểm bất kỳ trên mặt phẳng đáy\(ABCD\). Biết thể tích khối chóp\(O.MNPQ\)bằng\(V\). Tính thể tích khối chóp\(S.ABCD\).