Sách Toán - Học toán

Giải bài tập Toán từ lớp 1 đến lớp 12, Học toán online và Đề thi toán

Kết quả tìm kiếm cho: ty so

Đề: Cho hàm số:  $y = \frac{{{x^2} – x + 1}}{{x – 1}}$1)    Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2)    Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3)    Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:  $y = \frac{{{x^2} - x + 1}}{{x - 1}}$1)    Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2)    Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3)    Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$ Lời giải $1)$    Dành cho bạn đọc.$2)$    Tìm $A(0, b)$ là một điểm trên trục $Oy$ mà tiếp … [Đọc thêm...] vềĐề: Cho hàm số:  $y = \frac{{{x^2} – x + 1}}{{x – 1}}$1)    Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.2)    Tìm trên trục $Oy$ các điểm từ đó có thể kẻ được ít nhất một tiếp tuyến đến đồ thị $(C)$.3)    Xác định $a$ để đồ thị $(C)$ tiếp xúc với parabol $y = {x^2} + a$

Đề: Cho hàm số $f(x) = \frac{1}{3}x^3 – \frac{1}{2}(\sin a + \cos a){x^2} + \frac{3\sin 2a}{4}x$. Tìm a để hàm số đạt cực trị tại $x_1,x_2$ thỏa mãn điều kiện $x_1 + x_2 = x_1^2 + x_2^2$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số $f(x) = \frac{1}{3}x^3 - \frac{1}{2}(\sin a + \cos a){x^2} + \frac{3\sin 2a}{4}x$. Tìm a để hàm số đạt cực trị tại $x_1,x_2$ thỏa mãn điều kiện $x_1 + x_2 = x_1^2 + x_2^2$ Lời giải Ta có: \(f'(x) = {x^2} - (\sin a + c{\rm{os}}a)x + \frac{{3\sin 2a}}{4}\) Hàm số có CĐ, CT \( \Leftrightarrow f'(x) = 0\) có 2 nghiệm phân biệt \( \Leftrightarrow \Delta > 0 … [Đọc thêm...] vềĐề: Cho hàm số $f(x) = \frac{1}{3}x^3 – \frac{1}{2}(\sin a + \cos a){x^2} + \frac{3\sin 2a}{4}x$. Tìm a để hàm số đạt cực trị tại $x_1,x_2$ thỏa mãn điều kiện $x_1 + x_2 = x_1^2 + x_2^2$

Đề:  Cho hàm số : $f(x) = \sqrt {{sin^4}x + {cos ^4}x – 2msinxcos x} $Tìm các giá trị của m để $f(x)$ xác định với mọi $x.$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài:  Cho hàm số : $f(x) = \sqrt {{sin^4}x + {cos ^4}x - 2msinxcos x} $Tìm các giá trị của m để $f(x)$ xác định với mọi $x.$ Lời giải $f(x) = \sqrt {{{\sin }^4}x + {{\cos }^4}x - 2m\sin x\cos x} $ xác định với mọi x $\begin{array}{l} \Leftrightarrow {\sin ^4}x + {\cos ^4}x - 2m\sin x\cos x \ge 0\,\,\forall x\\ \Leftrightarrow 1 - 2{\sin ^2}x{\cos ^2}x - 2m\sin x\cos x … [Đọc thêm...] vềĐề:  Cho hàm số : $f(x) = \sqrt {{sin^4}x + {cos ^4}x – 2msinxcos x} $Tìm các giá trị của m để $f(x)$ xác định với mọi $x.$

Đề: Cho hàm số :$y = \frac{{(m + 1){x^2} – {m^2}}}{{x – m}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$2.$ Trong trường hợp tổng quát, chứng minh rằng với mọi giá trị $m \ne 0$, tiệm cận xiên của đồ thị hàm số luôn tiếp xúc với một Parabol cố định. Hãy chỉ rõ phương trình của Paralbol ấy.

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số :$y = \frac{{(m + 1){x^2} - {m^2}}}{{x - m}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$2.$ Trong trường hợp tổng quát, chứng minh rằng với mọi giá trị $m \ne 0$, tiệm cận xiên của đồ thị hàm số luôn tiếp xúc với một Parabol cố định. Hãy chỉ rõ phương trình của Paralbol ấy. Lời giải $1$. Dành cho bạn đọc tự giải.$2$. $y = \frac{{(m … [Đọc thêm...] vềĐề: Cho hàm số :$y = \frac{{(m + 1){x^2} – {m^2}}}{{x – m}}$$1$. Khảo sát sự biến thiên và vẽ đồ thị hàm số ứng với $m = 1.$$2.$ Trong trường hợp tổng quát, chứng minh rằng với mọi giá trị $m \ne 0$, tiệm cận xiên của đồ thị hàm số luôn tiếp xúc với một Parabol cố định. Hãy chỉ rõ phương trình của Paralbol ấy.

Đề: Hàm số $y=|x-97|$ có đạo hàm tại $x=97$ không? Tại sao?

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Hàm số $y=|x-97|$ có đạo hàm tại $x=97$ không? Tại sao? Lời giải Ta có:$\mathop {\lim }\limits_{\Delta x \to 0^{-}}\frac{f(97+\Delta x)-f(97)}{\Delta x}=\mathop {\lim }\limits_{\Delta x \to 0^-}\frac{|\Delta x|}{\Delta x}=-1  $$\mathop {\lim }\limits_{\Delta x \to 0^+} \frac{f(97+\Delta x)-f(97)}{\Delta x}= \mathop {\lim }\limits_{\Delta x \to … [Đọc thêm...] vềĐề: Hàm số $y=|x-97|$ có đạo hàm tại $x=97$ không? Tại sao?

Đề: Tìm giá trị nhỏ nhất của biểu thức:      $\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{c}}+\frac{c}{\sqrt{a}}$trong đó, các số dương $a,b,c $ thỏa mãn điều kiện $a+b+c\geq 3$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Tìm giá trị nhỏ nhất của biểu thức:      $\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{c}}+\frac{c}{\sqrt{a}}$trong đó, các số dương $a,b,c $ thỏa mãn điều kiện $a+b+c\geq 3$ Lời giải Đặt $A=\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{c}}+\frac{c}{\sqrt{a}}$Ta có: … [Đọc thêm...] vềĐề: Tìm giá trị nhỏ nhất của biểu thức:      $\frac{a}{\sqrt{b}}+\frac{b}{\sqrt{c}}+\frac{c}{\sqrt{a}}$trong đó, các số dương $a,b,c $ thỏa mãn điều kiện $a+b+c\geq 3$

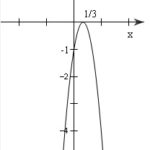
Đề: Vẽ đồ thị hàm số $y = – 9x^2 + 6x – 1$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Vẽ đồ thị hàm số $y = - 9x^2 + 6x - 1$ Lời giải Hướng dẫn:Trục đối xứng $x= - \frac{b}{2a} = \frac{1}{3} $Parabol có đỉnh $(- \frac{b}{2a};- \frac{\Delta}{4a})=(\frac{1}{3}, 0)$ Các điểm $(0; -1), (1; -4)$ thuộc đồ thị.Đồ thị  … [Đọc thêm...] vềĐề: Vẽ đồ thị hàm số $y = – 9x^2 + 6x – 1$

Đề: Cho $n$ là một số tự nhiên $ \ge 2$ và $a > 0$. Tìm giá trị lớn nhất của tổng $\sum\limits_{i = 1}^{n – 1} x_ix_{i + 1} $Trong đó $x_i\ge 0(i = 1,2,…,n),x_1 + x_2+ … + x_n = a$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho $n$ là một số tự nhiên $ \ge 2$ và $a > 0$. Tìm giá trị lớn nhất của tổng $\sum\limits_{i = 1}^{n - 1} x_ix_{i + 1} $Trong đó $x_i\ge 0(i = 1,2,...,n),x_1 + x_2+ ... + x_n = a$ Lời giải Giả sử ${x_k} = m{\rm{ax}}\left( {{x_1},{x_2},...,{x_n}} \right)$, khi đó ta có:$\begin{array}{l}\sum\limits_{i = 1}^{n - 1} {{x_i}{x_{i + 1}} = } \sum\limits_{i = 1}^{k - 1} … [Đọc thêm...] vềĐề: Cho $n$ là một số tự nhiên $ \ge 2$ và $a > 0$. Tìm giá trị lớn nhất của tổng $\sum\limits_{i = 1}^{n – 1} x_ix_{i + 1} $Trong đó $x_i\ge 0(i = 1,2,…,n),x_1 + x_2+ … + x_n = a$

Đề: Cho hàm số        $y = \frac{{u(x)}}{{v(x)}}$.  Chứng minh rằng nếu $y'({x_o}) = 0$ và $v'({x_o}) \ne 0$ thì ta có$\frac{{u'({x_o})}}{{v'({x_o})}} = \frac{{u({x_o})}}{{v({x_o})}}$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số        $y = \frac{{u(x)}}{{v(x)}}$.  Chứng minh rằng nếu $y'({x_o}) = 0$ và $v'({x_o}) \ne 0$ thì ta có$\frac{{u'({x_o})}}{{v'({x_o})}} = \frac{{u({x_o})}}{{v({x_o})}}$ Lời giải Ta có     $y' = \frac{{vu' - uv'}}{{{v^2}}}$, do đó:  $y'({x_o}) = 0 \Rightarrow v({x_o})u'({x_o}) - u({x_o})v'({x_o}) = 0{\rm{  }} \Leftrightarrow … [Đọc thêm...] vềĐề: Cho hàm số        $y = \frac{{u(x)}}{{v(x)}}$.  Chứng minh rằng nếu $y'({x_o}) = 0$ và $v'({x_o}) \ne 0$ thì ta có$\frac{{u'({x_o})}}{{v'({x_o})}} = \frac{{u({x_o})}}{{v({x_o})}}$

Đề: Cho hàm số:  $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$

Ngày Thuộc chủ đề:Bài tập Hàm số Tag với:

Đề bài: Cho hàm số:  $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$ Lời giải $1)$ Dành cho bạn đọc.$2)$ Giả sử có 2 … [Đọc thêm...] vềĐề: Cho hàm số:  $y = {x^3} + 3{x^2} + 3x + 5$.1) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.2) Chứng minh rằng trên đồ thị không tồn tại 2 điểm sao cho hai tiếp tuyến tại 2 điểm đó của đồ thị là vuông góc với nhau.3) Xác định k để trên đồ thị có ít nhất một điểm mà tiếp tuyến tại đó vuông góc với đường thẳng $y = kx$